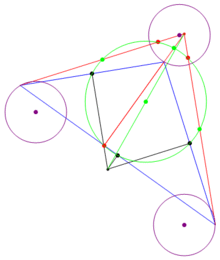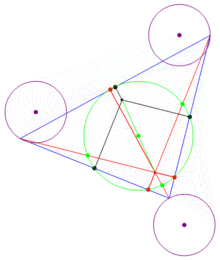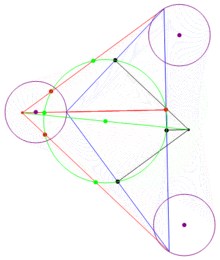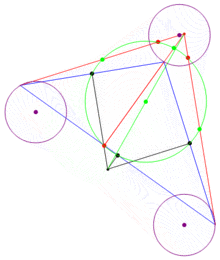
一個小小實驗︰辨識『印刷』的阿拉伯數字

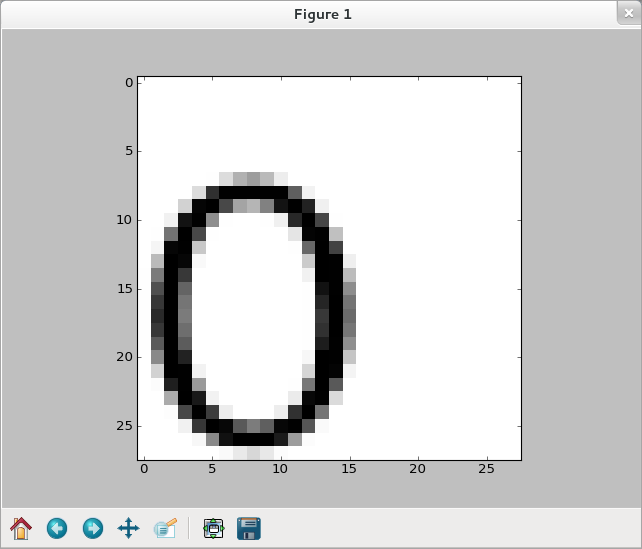
Figure 0_Gray

，竟然『network.py』會誤以為是『3』！！難道說『印刷』字能比『手寫』更難辨認的嗎？？或許答案就落在那個『0』是有『位移』的吧？？而那個小程式之『訓練』時用之『手寫數字』資料庫可都是計算過『圖心』的哩！！

THE MNIST DATABASE
of handwritten digits
Yann LeCun, Courant Institute, NYU
Corinna Cortes, Google Labs, New York
Christopher J.C. Burges, Microsoft Research, Redmond

……

The original black and white (bilevel) images from NIST were size normalized to fit in a 20×20 pixel box while preserving their aspect ratio. The resulting images contain grey levels as a result of the anti-aliasing technique used by the normalization algorithm. the images were centered in a 28×28 image by computing the center of mass of the pixels, and translating the image so as to position this point at the center of the 28×28 field.

───

因此『訓練』的『條件』以及『環境』也就決定了『network.py』所擅長之『辨識零點』的了！！？？如是看來人類的『視覺』當真是厲害得很也！！否則如何能作『幾何論證』乎？？豈能發現『九點圓』的呢？？！！

人們如何發掘『現象』間的『關係』？怎麼探討事物的『性質』？因何能發現且證明隱晦的『數學定理』？！也許讀讀維基百科上『九點圓』詞條一小段文本︰

九點圓

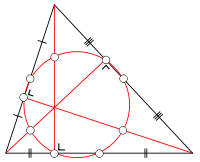
九點圓（又稱歐拉圓、費爾巴哈圓），在平面幾何中，對任何三角形，九點圓通過三角形三邊的中點、三高的垂足、和頂點到垂心的三條線段的中點。九點圓定理指出對任何三角形，這九點必定共圓。而九點圓還具有以下性質：

九點圓的半徑是外接圓的一半，且九點圓平分垂心與外接圓上的任一點的連線。
圓心在歐拉線上，且在垂心到外心的線段的中點。
九點圓和三角形的內切圓和旁切圓相切（費爾巴哈定理）。
圓周上四點任取三點做三角形，四個三角形的九點圓圓心共圓（庫利奇－大上定理）。

九點圓

Even if the orthocenter and circumcenter fall outside of the triangle, the construction still works.

歷史

1765年，萊昂哈德·歐拉證明：「垂心三角形和垂足三角形有共同的外接圓（六點圓）。」許多人誤以為九點圓是由而歐拉發現所以又稱乎此圓為歐拉圓。而第一個證明九點圓的人是彭賽列（1821年）。1822年，卡爾·威廉·費爾巴哈也發現了九點圓，並得出「九點圓和三角形的內切圓和旁切圓相切」，因此德國人稱此圓為費爾巴哈圓，並稱這四個切點為費爾巴哈點。庫利奇與大上分別於1910年與1916年發表庫利奇－大上定理「圓周上四點任取三點做三角形，四個三角形的九點圓圓心共圓。」這個圓還被稱為四邊形的九點圓，此結果還可推廣到n邊形。

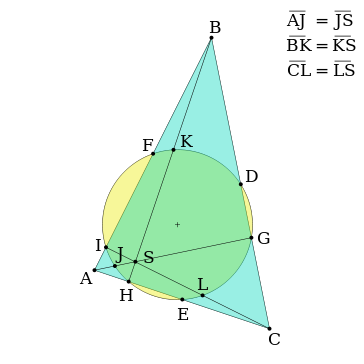
九點圓證明

如圖： $D$ 、 $E$ 、 $F$ 為三邊的中點， $G$ 、 $H$ 、 $I$ 為垂足， $J$ 、 $K$ 、 $L$ 為和頂點到垂心的三條線段的中點。

容易得出 $\triangle ABS \sim \triangle AFJ$ 、 $\triangle CBS \sim \triangle CDL$ （SAS相似）

因此 $\overline{FJ} // \overline{BH} // \overline{DL}$

同樣可得出 $\triangle ABC \sim \triangle FBD$ 、 $\triangle ASC \sim \triangle JSL$ （SAS相似）

因此 $\overline{FD} // \overline{AC} // \overline{JL}$

又 $\overline{BH} \perp \overline{AC}$ ，可得出四邊形 $DFJL$ 是矩形（四點共圓）

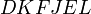同理可證 $FKLE$ 也是矩形（ $DKFJEL$ 共圓）

$\angle JLD = \angle JGD = 90^\circ$ ，因此可知 $G$ 也在圓上（圓周角相等）

同理可證 $H$ 、 $I$ 兩點也在圓上（九點共圓）

───

可以當成發想的起點。假使設想姑且不論到底是怎樣『發現』的，且談已經『被發現』後，是否人們就能容易了解那些『關係』、『性質』、以及『證明』呢？有人說︰閱讀『證明』容易，動手『證明』困難。似乎是講，既然都已理解了『證明』，焉有不曉『關係』與『性質』的耶！！若說條條大路通『羅馬』，就算盡觀了那些條條大路的景緻，和『羅馬』之風光能夠彼此比較的嗎？？！！更何況『始、中、終』的『學習』循環不斷，舊『終』則啟新『始』布線織網深化『閱歷』。所以『學問』浸潤良久總有所悟，宛如說今日這門古老的『幾何學』，是以前那門新創之『幾何學』的嗎！！？？

─── 摘自《勇闖新世界︰ W!o《卡夫卡村》變形祭︰品味科學‧教具教材‧【專題】 PD‧箱子世界‧九點圓》

更不要講或許人類還能超越『視覺了別』，創想『非歐幾何學』，試圖理解那『生之、育之』之大自然耶！！！

『歐幾里得』的『平行公設』 ── 經過『線外』一『點』，只能作一條『平行線』平行該『線』 ──，或許正因為不夠『直覺』，然而又有人將它看成了『公理』，於是乎長期以來議論不斷，如此經過了兩千多年。一八二零年時，俄國數學家『尼古拉‧伊萬諾維奇‧羅巴切夫斯基』 Никола́й Ива́нович Лобаче́вский 想用『歸謬法』證明︰假使僅『反對』了『平行公設』 ── 假設有兩條平行線 ── ，但是卻『保留』著『其它公設』，這樣的『幾何系統』是不是會發生內部之『邏輯矛盾』的呢？本來是想『證明』平行公設的『必要性』，結果意外『成立』了一門『新的幾何學』，這就是第一個被提出的『非歐幾何學』。如果從『羅氏幾何學』建構方法來看，我們可以『知道』只要『選擇』邏輯上不矛盾的『一些公理』都有可能『成立』一種『幾何學』。這樣我們的『大自然』它會『選擇』特定的『幾何學』的嗎？假使果真有這個『幾何學』，我們又要『依據』什麼才能『判斷』它是『真實』的呢？？因此我們或許更當細思『先驗知識』與『後驗知識』之間的大哉『辯』與『辨』的吧！！

三種平行假設

笛沙格定理

如果A.a，B.b，C.c 共點，那麼 (A.B)∩(a.b)，(A.C)∩(a.c)，(B.C)∩(b.c) 共線。

雙曲面幾何學
多條平行線

球面幾何學
沒有平行線

假使對『大自然』的『認識』就像是『知識之拼圖』，作為一個科學的『觀察者』，通常需要『考察』那些『已知的碎片』能不能夠『融匯』成為那一整張『全景圖』，往往還得『研判』以為『拼起的圖象』它會不會『引發』彼此之間『不同調』的『矛盾』。終究『科學』以『實驗觀察』之『現象事實』為『依據』，從所得之『量測數據』建立『假說』，提出『理論』來『解釋』自然萬象。要是『輕忽』了這個『本末』，可能會將『物理方程式』只當成了『數學系統』來『研究』，『忘卻』了『物理量』本是為著『描述自然』而『有』的，如果說『宇宙』中根本『沒有』那種量，它又怎麼能有『物理意義』的呢？比方講，從日常生活的『經驗』裡，我們『知道』拋一個『球』，它總是會『停下來』的。於是在『力學』中有所謂的『摩擦力』用以『說明』它的『原因』。然而不同的『形狀』、相異的『接觸面』以及物體『速度大小』種種『因素』都可能影響這個『摩擦力』的大小。假使從『物理近似』的觀點來看，假設那個『摩擦力大小』正比於『速度大小』，方向與『運動方向』相反，『數學上』表示為 $f_r = - \alpha \cdot v, \ \alpha > 0$ 。這個『函數』符合物理上『摩擦力』的『想法』︰

一、 $v = 0 \Longrightarrow f_r = 0$

二、 $v > 0, \Longrightarrow f_r < 0$

三、 $v < 0, \Longrightarrow f_r > 0$

，於是我們會想 $f_r = - \beta \cdot v^2, \ \beta > 0$ 這個『形式』的『摩擦力』應該『不合理』的了。為什麼呢？因為當 $v < 0$ 時 $f_r < 0$ ，那個『摩擦力』總『不可能』產生『加速』的吧！然而當我們將物理的『運動方程式』用『數學』來表達時，它就是一個『數學方程式』了，如果只就它的『數學求解』而言，那麼它的『數學近似』應該是『合理的』吧！這樣我們當考慮『摩擦力』的『修正項』時，假設它是 $\pm \beta \cdot v^2$ 這在物理上『合理的』嗎？簡單分析一下 $f_r = - \alpha \cdot v \pm \beta \cdot v^2, \ \alpha , \beta > 0$ ，當 $f_r = 0$ 時，它有兩個『解』 $v = 0, v = \pm \frac{\alpha}{\beta}$ ，它雖然不可能在速度之『全域』上『符合』物理上對『摩擦力』的想法，不過某個速度的『範圍』內，它的確是『符合』的啊！如此到底就『物理近似』的『意義』來講，這個『範圍限定』是『可』還是『不可』的呢？如果審思『物理量』的『和』 ⊕ 應該如何『計算』，是由『自然律』得來的，因此它在『意義』上就與『數學的加』＋有一定的『不同』。也可以說『數學近似』的『過程結果』，一般還是需要『合理的』物理之『解釋』。要是說因為 $f_r = - \alpha \cdot v - \beta \cdot v^2 - \gamma \cdot v^3$ 可以在速度的『全域』上『符合』物理上對『摩擦力』的想法，所以在物理上它就比 $f_r = - \alpha \cdot v, \ \alpha > 0$ 是更好的『近似描述』，豈不怪哉！！