過去作文曾有所謂『起承轉合』之論，然而天下文章天下人寫，又何必拘泥於『套式』的呢？倘若一招半式尚未學習，又何彷拘泥於『套式』的呢！終究寫作者之表述，需要閱讀者能明白，所以詞能達意、議論清楚、文字通順 …… 其初始，足矣哉。

有答之問之所生，或在原理不能貫通、習焉而未能察、概念內蘊尚無法甚解 …… ，因作此破題之問︰

【既知】

假使一個任意複雜之光學系統竟能夠『等效』於一片『薄透鏡』豈非太美妙耶！且聽聽 Justin Peatross 和 Michael Ware 先生們之大哉論也

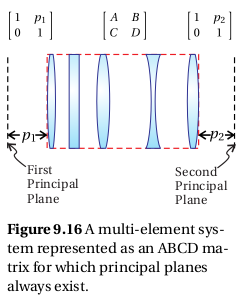
※ 註︰ 若一光學系統光線進、出介質折射率相同，則

。

顯然 不等於零。

─── 摘自《光的世界︰矩陣光學六戊》

 

【已知】

前三篇文本中，我們談了一般『光學矩陣』

只要 ，都可借著『自由空間』

化成一個等效之『薄透鏡』

。

因此在『主平面』之參考系裡，分享著同樣的『成像公式』

，具有相同『成像條件』， 參數為

。

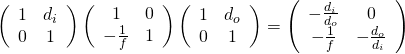甚至可以『串接成像』

的矣！如是就確定了參數 之『聚焦』地位，以及參數 的『影像縮放』性質！！

─── 摘自《光的世界︰矩陣光學六庚》

 

【且知】

現象既因相距 之兩透鏡之組合而起︰

物 → 光 …… → 透鏡 → 距離 → 透鏡 …… → 像

且先列出其『光學矩陣』表達式︰

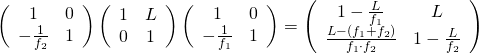
已知若其『等效』於『薄透鏡』，焦距 等於 。所以曉

‧ 時， 。

‧ 或 時，組合焦距可由該式算出。

因是問題就落在 的時候了。但思此刻之前、之後恰是 變號之際，也是組合透鏡或聚、或散性質變化之處，故而特殊的耶！！？？

─── 摘自《光的世界︰矩陣光學六壬》

 

莫非是原理不足以解釋現象成因的呢？？還是條件太過複雜以至於難以解析耶！！或因為『薄透鏡』之理想性而想入非非的乎︰

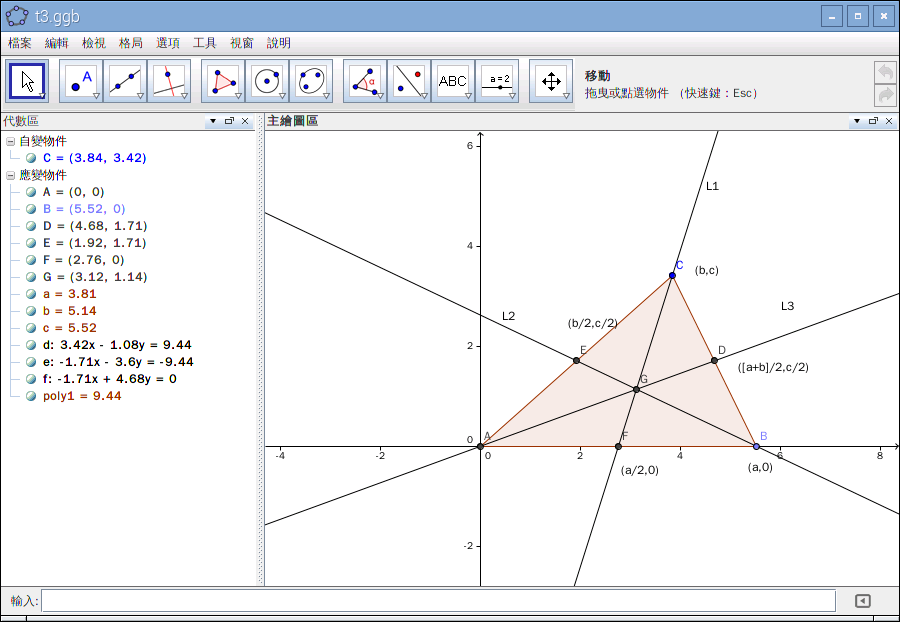
若問為什麼平面上的一個一般三角形可以如下圖表示

， 只用著 三個參數？即使在思考過 是『底』之『長』， 是此『底』之『高』， 是此『高』距與此『底』一端的距離。我們深信這就『確定』了那個三角形。然而若再問︰如果此三角形的三個頂點用更一般的   、 、 來表達 ，如是分明有六個參數。那麼這兩種『表述』當真是一樣的嗎？設想你在桌面上『移動』一個三角形，從此『位置』此『方位』到達彼『位置』彼『方位』，你會認 為這個三角形『改變』了嗎？？假使『直覺』以為『不變』，這個三角形就必得有使之『不變』的『因由』，這個『因由』不必『參照』解析幾何的『座標』而確立 。或可說它就是歐式幾何一個三角形的『定義』內涵而已。如此而言，一個『確定』的三角形，可由它的三個『邊長』來『確立』，所以六個參數補之以三個確定之 邊長關係，豈非還是三個參數的耶？？

因為這個『歐式幾何』的『留白』，常使人懷疑『解析幾何』簡化『座標系』的『選擇』，到底『圖形』的『自由度』是幾何的了。說難道易，就請讀者思索︰平面上的『 □ 』與『 ○ 』，到底一方一圓需要幾個參數來描述的呢？

從物理上講，那個三角形就是『剛體』 rigid body ，它在『運動』中保持『形狀』的『不變性』。

─── 摘自《勇闖新世界︰ W!o《卡夫卡村》變形祭︰品味科學‧教具教材‧【專題】 PD‧箱子世界‧留白》

 

現象之理則的推演千絲萬縷，其歸結唯一而已矣☆