減字木蘭花〈寄田不伐〉‧吳則禮

星星素髪只有鳴笳樓上發
㸔舞胡姬待得平安探騎歸
故人漸老只與虎頭論黒妙
懐抱難開快遣披雲一笑來
梅花未徹付與團團沙塞月
端欲捐書去乞君王丈二殳
貂裘錦㡌盤馬不甘青鬢老
底事偏衣細草平沙㸔打圍
河西春晚獨有栁條來入眼
塞水斜斜不道欺寒紅杏花
邊笳初發與喚團團孤塞月
鴈響連天誰倚城頭百尺欄

平安夜前讀文章，是否寧靜以致遠？

Julius Orion Smith III 先生以幾何

Geometric Signal Theory

This chapter provides an introduction to the elements of geometric signal theory, including vector spaces, norms, inner products, orthogonality, projection of one signal onto another, and elementary vector space operations. First, however, we will “get our bearings” with respect to the DFT.

解離散傅立葉變換

※

$-j \cdot w_k \cdot t_n = -j \cdot k \cdot \Omega \cdot n \cdot T = -j \cdot k \cdot \frac{2 \pi}{N} \cdot f_s \cdot n \cdot T$

$= -j \cdot k \cdot \frac{2 \pi}{N \cdot T} \cdot n \cdot T = -j \cdot k \cdot \frac{2 \pi}{N} \cdot n = -j \cdot \frac{2 \pi \cdot n \cdot k}{N}$

可得 $N$ 維空間直觀義！茲取

$s_k [n] = e ^{j \cdot \omega_k \cdot t_n} , \ n = 0 \cdots N-1$

$= e^{j \frac{2 \pi \cdot k \cdot n}{N}$ ※ $\left( s_k [n] \right)^N = 1$

為向量

$\vec{s_k}, \ k = 0 \cdots N-1$

$= \left( 1, e^{j \frac{2 \pi \cdot k}{N} \cdot 1}, e^{j \frac{2 \pi \cdot k}{N} \cdot 2}, \cdots , e^{j \frac{2 \pi \cdot k}{N} \cdot (N-1)} \right)$

之第 $n$ 個分量。

那麼在此空間裡定義內積運算︰

$\langle \vec{s_k} , \vec{s_l} \rangle = \sum \limits_{n=0}^{N - 1} e^{j \frac{2 \pi \cdot k}{N} \cdot n} \cdot \overline{e^{j \frac{2 \pi \cdot l}{N} \cdot n}}$

內積空間

內積空間是數學中的線性代數裡的基本概念，是增添了一個額外的結構的向量空間。這個額外的結構叫做內積或純量積。內積將一對向量與一個純量連接起來，允許我們嚴格地談論向量的「夾角」和「長度」，並進一步談論向量的正交性。內積空間由歐幾里得空間抽象而來（內積是點積的抽象），這是泛函分析討論的課題。

內積空間有時也叫做准希爾伯特空間（pre-Hilbert space），因為由內積定義的距離完備化之後就會得到一個希爾伯特空間。

在早期的著作中，內積空間被稱作么正空間，但這個詞現在已經被淘汰了。在將內積空間稱為么正空間的著作中，「內積空間」常指任意維（可數或不可數）的歐幾里德空間。

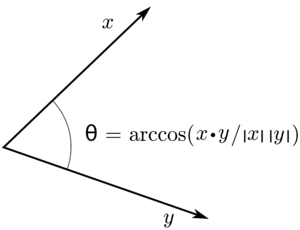
Geometric interpretation of the angle between two vectors defined using an inner product

定義

下文中的純量域 $F$ 是指實數體 $\mathbb {R}$ 或複數域 $\mathbb {C}$ 。

正式地，一個內積空間是域 $F$ 上的向量空間 $V$ 與一個內積(即一個映射)構成的。 $V$ 上的一個內積定義為正定、非退化的共軛雙線性形式（ $F = \mathbb{R}$ 時，內積是一個正定、對稱、非退化的雙線性形式），記為 $\langle \cdot, \cdot \rangle : V \times V \rightarrow F$

它滿足以下設定：

共軛對稱； $\forall x,y\in V, \; \; \langle x,y\rangle =\overline{\langle y,x\rangle}.$

這個設定蘊含了： $\forall x \in V, \; \; \langle x,x\rangle \in \mathbb{R}$ ，因為 $\langle x,x\rangle = \overline{\langle x,x\rangle}$ .
對第一個元素線性； $\forall a\in F,\ \forall x,y\in V,\ \langle ax,y\rangle= a \langle x,y\rangle, \quad \forall x,y,z\in V,\ \langle x+y,z\rangle= \langle x,z\rangle+ \langle y,z\rangle.$

由前兩條可以推斷出： $\forall b\in F,\ \forall x,y\in V,\ \langle x,by \rangle= \overline{b} \langle x,y\rangle, \quad \forall x,y,z\in V,\ \langle x,y+z\rangle= \langle x,y\rangle+ \langle x,z\rangle.$

因此 $\langle \cdot , \cdot \rangle$ 實際上是一個半雙線性形式。
非負性： $\forall x \in V,\ \langle x,x\rangle \ge 0.$
非退化：從V到對偶空間V*的映射： $x\mapsto \langle x,\cdot\rangle$ 是同構映射。

在有限維的向量空間中，只需要驗證它是單射： $\langle x,y\rangle = 0 \; \forall y \in V \,$ 若且唯若 $x = 0 \,$ 。

擁有以上性質的共軛雙線性形式被稱為埃爾米特形式。內積是一個埃爾米特形式。

如果 $F$ 是實數體 $\mathbb {R}$ 那麼共軛對稱性質就等價於對稱性： $\langle x,y\rangle=\langle y,x\rangle.$ ，也就是說，共軛雙線性變成了一般的雙線性。

能夠證明

如果 $k \neq l$

$\langle \vec{s_k} , \vec{s_l} \rangle = \sum \limits_{n=0}^{N - 1} e^{j \frac{2 \pi \cdot k}{N} \cdot n} \cdot \overline{e^{j \frac{2 \pi \cdot l}{N} \cdot n}}$

$= \sum \limits_{n=0}^{N - 1} \left[ e^{j \frac{2 \pi \cdot (k-l)}{N}} \right]^n$ ※ 幾何級數

$= \frac{1-e^{j \cdot 2 \pi \cdot (k-l)}} {1 - e^{j \frac{2\pi \cdot (k-l)}{N}}}$

$=0$ 正交也。

如果 $k = l$

$\langle \vec{s_l} , \vec{s_l} \rangle = \sum \limits_{n=0}^{N - 1} e^{j \frac{2 \pi \cdot l}{N} \cdot n} \cdot \overline{e^{j \frac{2 \pi \cdot l}{N} \cdot n}}$