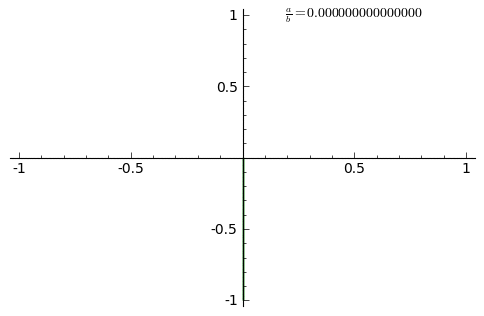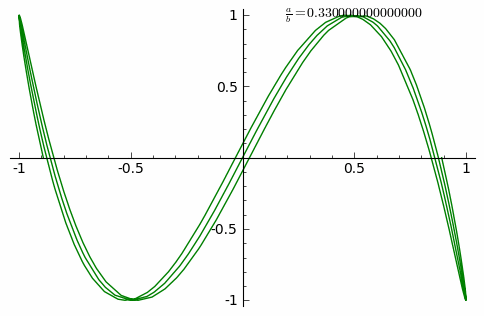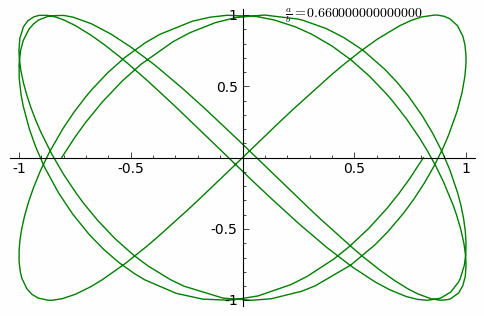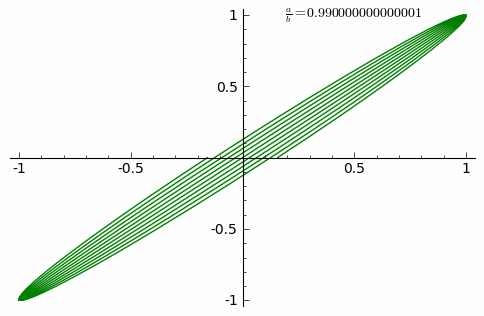通常回朔歷史
純律
純律 與十二平均律、五度相生律為音樂的三種主要律式。它通過大三度和純五度的組合變化來確定音階中各音的音高。由於在這種音階中 ,主音與其它音的關係都是純音程的關係[1],故人耳聽起來效果顯得和諧,得名純律。
原理
按照大三和弦關係’依次產生音序(五聲,七聲,12音)的生律方式, 例如: 純五度加大三度組成大七度;純五度減大三度組成小三度[2]。
該方法產生的音階與十二平均律、五度相生律有著細微的差異。純律與五度相生律均基於自然泛音音程[2],這是它們不同於十二平均律之處。
純率即取1、 (或
)、
、
(或
)、
(或
)、
、
(或
、
)、
、
(或
)、
(或
)、
(或 }
)、
(或
)、2為數列。
歷史
考察 □ ○ 由來
五度相生律
原理
按照自然泛音的純五度關係依次產生音序(5聲,7聲,12音)的生律方式,該方法產生的音階與十二平均律有著細微的差異。
- 取一基準音,在此以C為例,將其頻率f乘上3/2,即升高完全五度得下一音G。
- 再將G升高完全五度得下一音D,此時D之頻為(3f/2)*(3/2)=9f/4,高於原基準音之倍頻,故將其除二,即降八度得9f/8。
- 再將D升高完全五度得下一音A,此時A之頻為(9f/8)*(3/2)=27f/16。
- 再將A升高完全五度得下一音E,此時E之頻為(27f/16)*(3/2)=81f/32,高於原基準音之倍頻,故將其降八度得81f/64。
- 再將E升高完全五度得下一音B,此時B之頻為(81f/64)*(3/2)=243f/128。
- 假設有一音升高完全五度再降八度後為基準音C,可得此音之頻為4f/3,此即為F。
依上法可得七聲音階,茲整理為下表。
| 音階 | C | D | E | F | G | A | B | C | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 與基頻之比 | 1/1 | 9/8 | 81/64 | 4/3 | 3/2 | 27/16 | 243/128 | 2/1 | ||||||||
| 與前音之比 | — | 9/8 | 9/8 | 256/243 | 9/8 | 9/8 | 9/8 | 256/243 | — | |||||||
按照五度音列向上(下)n個音的一般公式如下:(BM=基準音頻率,n=相生次數)
歷史沿革
總至傳說耶!?
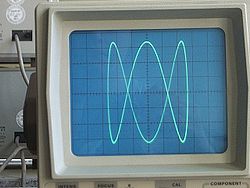
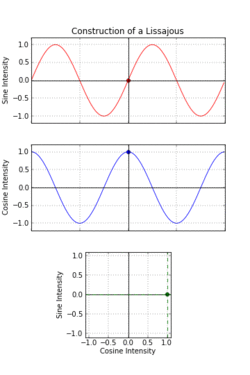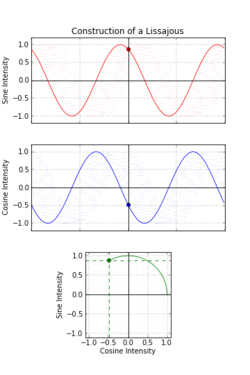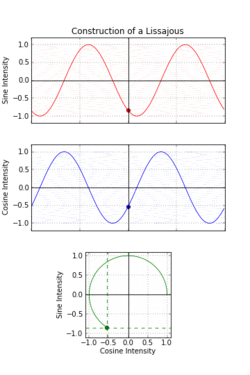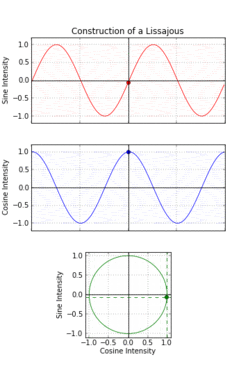
一八一五年納撒尼爾‧鮑迪奇 Nathaniel Bowditch 首先研究了『一族曲線』,它是兩個沿著『互相垂直』方向的『正弦振動』之合成的『軌跡』。一八五七年朱爾‧安托瓦內‧利薩茹 Jules Antoine Lissajous 作了詳細研究。他同時利用『一束光』射向固定在一個『音叉』上的『鏡子』,再將『反射光』又導往固定在另一個『音叉』上的一面『鏡子』,之後的這一個音叉的振動方向與之前的那一個垂直,一般所使用的振動頻率也不同,最終反射光就在牆上形成了今天所說的『利薩茹圖形』。假使從『音樂』的角度來看,這就是兩個『音符』同奏或接續時,所產生的一種特定的『頻率』harmonic interval 之間『和諧』與否的關係!!
數學上,利薩茹 Lissajous 曲線可以用『參數方程式』表示為
![]()
![]()
這族曲線的『外貌』與兩個振動之『頻率比』![]() 有很大的關係。如果它是最簡『有理數』
有很大的關係。如果它是最簡『有理數』![]() ,此處
,此處 ![]() 是自然數,這條曲線是靜止『封閉的』,在
是自然數,這條曲線是靜止『封閉的』,在 ![]() 軸上有
軸上有 ![]() 個『波瓣』,以及在
個『波瓣』,以及在 ![]() 軸上有
軸上有 ![]() 個『波瓣』。假使比值是『無理數』,這條曲線看起來在『旋轉』。兩振動的『振幅 』之比值
個『波瓣』。假使比值是『無理數』,這條曲線看起來在『旋轉』。兩振動的『振幅 』之比值 ![]() 確定了此曲線相對的『長與寬』;兩振動之間的『相位差』
確定了此曲線相對的『長與寬』;兩振動之間的『相位差』 ![]() 決定了曲線外貌的『旋轉角』。
決定了曲線外貌的『旋轉角』。
傳說中畢達哥拉斯發現『音律』有一段美麗的故事。有一天他偶然經過『打鐵鋪』店門口,卻為『打鐵』時有『節奏』而且『悅耳』的聲音所吸引。他感覺到很『驚奇』,於是走進了鋪中『觀察』,『研究』後發現四個『打鐵錘』的『重量比』恰為 『12:9:8:6』。假使將之兩兩一組拿來敲打,『12: 6= 2:1』、『12 : 8 = 9:6 = 3:2』和『12:9=8:6=4:3』的組合都能發出『和諧』的聲音。之後畢達哥拉斯更進一步用『弦琴』來做『實驗』並且加以『驗證』,這就是著名之『弦琴律』的由來 !!
如果在一台『示波器』上 ![]() 輸入
輸入 ![]() 軸信號,
軸信號,![]() 輸入
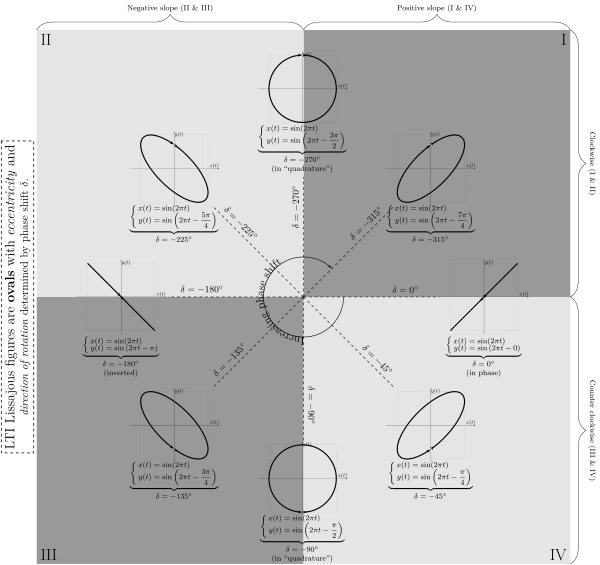
輸入 ![]() 軸信號,這時你就可以用示波器來觀察它所顯示的曲線,並且衡量出這兩個信號的『頻率比』以及『相位差』。在專業聲音的領域 ,通常利薩茹曲線用來分析『左右』聲道的『立體聲信號』stereo audio signal 之間的『相位關係』。假使你正研究一個『線性非時變系統』的『電路』,因此『輸入信號』的頻率就一定會與『輸出信號』的頻率『相同 』。由於物理的『因果原理』要求『輸出信號』發生在『輸入信號』之後,所以輸出入間的『相位關係』將如左圖所示,應當都是『負值』。這個情況下,你可以相當『精確』的『測量』相位差,也就是說這個 LTI 系統的『響應遲延』。
軸信號,這時你就可以用示波器來觀察它所顯示的曲線,並且衡量出這兩個信號的『頻率比』以及『相位差』。在專業聲音的領域 ,通常利薩茹曲線用來分析『左右』聲道的『立體聲信號』stereo audio signal 之間的『相位關係』。假使你正研究一個『線性非時變系統』的『電路』,因此『輸入信號』的頻率就一定會與『輸出信號』的頻率『相同 』。由於物理的『因果原理』要求『輸出信號』發生在『輸入信號』之後,所以輸出入間的『相位關係』將如左圖所示,應當都是『負值』。這個情況下,你可以相當『精確』的『測量』相位差,也就是說這個 LTI 系統的『響應遲延』。
在沒有『示波器』的時代,有一種使用『單擺』的機械『繪圖工具』,稱之為『諧振記錄器』harmonograph。大約在十九世紀中葉出現,傳聞是英國蘇格蘭格拉斯哥大學 University of Glasgow 數學教授休‧布来克本 Hugh Blackburn 所發明的。一個簡單『橫向的』 lateral 諧振記錄器上的兩個『阻尼單擺』運動方程式,可以數學上表示為
![]()
![]()
,式中 ![]() 是『幅度大小』、
是『幅度大小』、![]() 是『角頻率』、
是『角頻率』、![]() 是『相位角』以及
是『相位角』以及 ![]() 為『阻尼常數』。在這個裝置上
為『阻尼常數』。在這個裝置上 ![]() 控制『繪圖筆』的
控制『繪圖筆』的 ![]() 軸運動 ,
軸運動 ,![]() 控制『繪圖板』的
控制『繪圖板』的 ![]() 軸運動,通常繪出的圖形也是『利薩茹』一類的相關曲線。
軸運動,通常繪出的圖形也是『利薩茹』一類的相關曲線。
二零一一年 JM Gustafson 先生發表了一個『虛擬的』諧振記錄器模擬軟體,有興趣的讀者可以到那兒去『玩玩』,嘗試設計不同的『單擺參數』,『創造』自己喜歡的『美麗曲線』!!
─── 摘自《萬花尺 Spirograph Art》
故耳承先啟後者,往往有問題待解乎?!
在《【Sonic π】聲波之傳播原理︰共振篇《四下》》文本裡,我們談到了一根『半波長』之『估量的尺』,意在表明『欣賞自然』與『理解科學』的『靜觀自得』之境。此境將周遭萬象與人『關聯』起來,於是我們可以更深入的認識『自然』與『人造』物的世界︰
波的傳播除了『頻率』之外,『波長』也是重要的因素,尤其在考慮波的『輻射』與『散射』現象的時候。常溫下聲波速度約為 343.2 米/秒,從一個『邊長』是 ![]() 的共振腔共振時『半波長』的『整數倍』來看,它是否可以用來度量『聲源』的『尺寸』大小的呢?假使以『音律』中『十二平均律』的鋼琴『中央 C』261.6 赫茲來作計算,聲波波長大約是 1.312 米。『紅嘴相思鳥』鳴叫聲,以基本音調為主,頻率範圍大約為 2.50 ~ 3.80 千赫,主峰在 1.82 千赫,波長是 18.86 公分。當一隻鳥在發現略食者在周遭時,會發出警告同伴的鳴叫聲,它的頻率大約是 7000 Hz,波長約為 4.90 公分。『蟋蟀』的蟲鳴聲頻率範圍很廣 3 ~ 50 千赫,通常是相當純的律音,主峰在四、五千赫,次峰在十四千赫。以主峰 4.5 千赫計算大約 7.63 公分。 『人類』的發聲頻率範圍約為 85 ~ 1100 赫茲,假使說以低音 85 赫茲來講,波長為 4.04 米;『狗』的發聲頻率範圍是 452~ 1800 赫茲,波長是 75.93 公分;『貓』的發聲頻率範圍是 760 ~ 1500 赫茲,波長是 45.15 公分。如此看來『半波長』果然可以看成一根『估量的尺』,假使一個物體沒有明顯的『長寬高』,比方說像一個『球』,它的共振波長
的共振腔共振時『半波長』的『整數倍』來看,它是否可以用來度量『聲源』的『尺寸』大小的呢?假使以『音律』中『十二平均律』的鋼琴『中央 C』261.6 赫茲來作計算,聲波波長大約是 1.312 米。『紅嘴相思鳥』鳴叫聲,以基本音調為主,頻率範圍大約為 2.50 ~ 3.80 千赫,主峰在 1.82 千赫,波長是 18.86 公分。當一隻鳥在發現略食者在周遭時,會發出警告同伴的鳴叫聲,它的頻率大約是 7000 Hz,波長約為 4.90 公分。『蟋蟀』的蟲鳴聲頻率範圍很廣 3 ~ 50 千赫,通常是相當純的律音,主峰在四、五千赫,次峰在十四千赫。以主峰 4.5 千赫計算大約 7.63 公分。 『人類』的發聲頻率範圍約為 85 ~ 1100 赫茲,假使說以低音 85 赫茲來講,波長為 4.04 米;『狗』的發聲頻率範圍是 452~ 1800 赫茲,波長是 75.93 公分;『貓』的發聲頻率範圍是 760 ~ 1500 赫茲,波長是 45.15 公分。如此看來『半波長』果然可以看成一根『估量的尺』,假使一個物體沒有明顯的『長寬高』,比方說像一個『球』,它的共振波長 ![]() 正比於『體積立方根』也就是『想當然耳』的了!!
正比於『體積立方根』也就是『想當然耳』的了!!
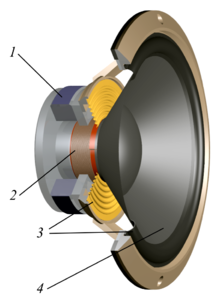
然而人的『聽覺範圍』是從 20 到 20k Hz,一個二十赫茲的聲音波長有 十七點一六米那麼長,這樣一個『音響喇叭』又要多大才能夠『共振』的呢?因為即使對『中央 C』來講,半波長也有 65.6 公分那麼長。所以一般動力『揚聲器』Loudspeaker 是用『聲波輻射』原理來設計的。
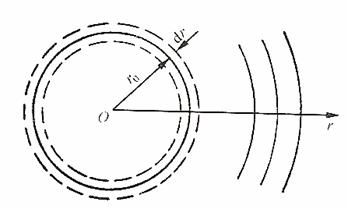
聲學裡一個『脈動球』 Pulsataing Sphere 『聲源』
是一個『半徑』在 ![]() 附近
附近 ![]() 以『頻率』
以『頻率』![]() 作『簡諧振動』的球,假使球的半徑遠小於聲波『波長』
作『簡諧振動』的球,假使球的半徑遠小於聲波『波長』![]() ,多個波長距離之外的遠處『聲場強度』
,多個波長距離之外的遠處『聲場強度』![]() ,此處
,此處 ![]() 是聲源振幅。其實假使
是聲源振幅。其實假使 ![]() 它可以看成『點聲源』,比方講這就可以計算典型『揚聲器』的圓形『振動膜』所產生的『聲場』。因此也就可以了解為了追求『高傳真』 HiFi 的『聲音品質』,揚聲器分開了『高音』、『中音』以及『低音』喇叭設計的原故。以及現今為了加強『影音』的『震撼力』與『臨場感』採用杜比 AC3 5.1 規格,它有五個『喇叭』加上一個『超重低音』音箱的因由。
它可以看成『點聲源』,比方講這就可以計算典型『揚聲器』的圓形『振動膜』所產生的『聲場』。因此也就可以了解為了追求『高傳真』 HiFi 的『聲音品質』,揚聲器分開了『高音』、『中音』以及『低音』喇叭設計的原故。以及現今為了加強『影音』的『震撼力』與『臨場感』採用杜比 AC3 5.1 規格,它有五個『喇叭』加上一個『超重低音』音箱的因由。
當人們在戶外,有時『拗著手』作『大聲公』狀來『叫人』,它是可以用『共振』和『輻射』來作解釋的嗎?每當夜深人靜時,『蟲鳴鳥叫』聲又為什麼會『擾人清夢』的呢??
也許越『理解』大自然,人們就越可能『欣賞』大自然的『美』吧!又或許果真是『處處靜觀皆自得』的啊!!
───
若是人們知道『十二平均律』發現的歷史︰
十二平均律
十二平均律,又稱十二等程律,是一種音樂的定律方法,將一個八度平均分成十二等份,每等分稱為半音,是最主要的調音法。
歷史
公元 400 年左右,中國南朝數學家何承天提出世界歷史上最早有記載的十二平均律數列 900 849 802 758 715 677 638 601 570 536 509.5 479 450(原文:……黃鐘長九寸,太簇長八寸二厘,林鐘長六寸一厘,應鐘長四寸七分九厘強)[1] .
義大利的物理學家伽利略·伽利萊的父親伽利略·文森佐曾試圖解決十二平均率問題,但他用的倍率是 18:17 而不是![\sqrt [12] {2}](https://upload.wikimedia.org/math/7/0/b/70b8b8fc763c20423a65bd934e378085.png) ,因此自乘12次後只得 1.98556,不是2,八度走了音,他的系統只可算近似十二音階平均律[2]
,因此自乘12次後只得 1.98556,不是2,八度走了音,他的系統只可算近似十二音階平均律[2]
1605年荷蘭數學家西蒙·斯特芬在一篇未完成的手稿「Van de Spiegheling der singconst」[3]提出用![\sqrt [12] {1/2}](https://upload.wikimedia.org/math/e/7/a/e7a14fb08396757b493af39425a5917d.png) 計算十二平均律,但因計算精度不夠,他算出的弦長數字,有些偏離正確數字一至二單位之多[4]
計算十二平均律,但因計算精度不夠,他算出的弦長數字,有些偏離正確數字一至二單位之多[4]
西蒙·斯特芬的弦長表[5]
| 音 | 弦 10000 | 比率 | 正確的弦長 |
|---|---|---|---|
| 半音 | 9438 | 1.0595465 | 9438.7 |
| 全音 | 8909 | 1.0593781 | |
| 1.5 音 | 8404 | 1.0600904 | 8409 |
| 2 倍全音 | 7936 | 1.0594758 | 7937 |
| 2.5 音 | 7491 | 1.0594046 | 7491.5 |
| 3 音 | 7071 | 1.0593975 | 7071.1 |
| 3.5 音 | 6674 | 1.0594845 | 6674.2 |
| 4 音 | 6298 | 1.0597014 | 6299 |
| 4.5 音 | 5944 | 1.0595558 | 5946 |
| 5 音 | 5611 | 1.0593477 | 5612.3 |
| 5.5 音 | 5296 | 1.0594788 | 5297.2 |
| 八度 | 1.0592000 |
西蒙·斯特芬的頻率比,每音一率,且各不相同,這是不正確的[6]
朱載堉發明十二平均律
中國明代音樂家朱載堉於萬曆十二年(1584年)首次提出「新法密率」(見《律呂精義》、《樂律全書》),推算出以比率 ![\sqrt [12] {2}](https://upload.wikimedia.org/math/7/0/b/70b8b8fc763c20423a65bd934e378085.png) 將八度音等分為十二等分的算法,並製造出十二平均律律管及律準,是世界上最早的十二平均律樂器。他用九九八十一位算盤計算出來準確到25位數字新法密率為:
將八度音等分為十二等分的算法,並製造出十二平均律律管及律準,是世界上最早的十二平均律樂器。他用九九八十一位算盤計算出來準確到25位數字新法密率為:
| 律名 | 比率 |
|---|---|
| 正黃鐘 | 1.000000000000000000000000 |
| 倍應鍾 | 1.059463094359295264561825 |
| 倍無射 | 1.122462048309372981433533 |
| 倍南呂 | 1.189207115002721066717500 |
| 倍夷則 | 1.259921049894873164767211 |
| 倍林鍾 | 1.334839854170034364830832 |
| 倍蕤賓 | 1.414213562373095048801689 |
| 倍仲呂 | 1.498307076876681498799281 |
| 倍姑洗 | 1.587401051968199474751706 |
| 倍夾鍾 | 1.681792830507429086062251 |
| 倍太蔟 | 1.781797436280678609480452 |
| 倍大呂 | 1.887748625363386993283826 |
| 倍黃鐘 | 2.000000000000000000000000 |
───
自將更能了解『 MIDI 碼』之制定與『十二平均律』的關係︰
MIDI 碼 = ![]()
進 而明白『鋼琴』琴鍵安排的規律。這一切的種種都離不開人類的『聽覺』,自然也沒有古今東西之人性差異。憑藉『感官知覺』之天賦,人們區分了『聲』與 『樂』,『光』和『色』,居處於聲光樂色如斯美好的宇宙。這也許也說明了『感覺』終究是『物理』以及『心理 』之『統覺』的吧!那根『豆芽』之理竟如是難啃的耶?所以我們需要『聽得見』又『看得到』的『學習環境』來『體驗』那既『具體』又『抽象』之『感覺』實在 的乎!?
也許一個『拍頻』 beat note 『現象』之問題,足以表達那難言之隱的吧!!假使回答以
差頻(英文:beat note)一詞來源於聲學上兩個頻率相近但不同的聲波的干涉,所得到的干涉信號的頻率是原先兩個聲波的頻率之差 ,因此叫做差頻。
───
,怕是難明究理。即使再補之以
……… 摘自《Sonic π 之節拍體驗》
此所以寫在調音系統
筆記之前也☆