由於 SymPy 使用『向量外積』定義並矢張量︰


※ 參閱
外積
外積(英語:Outer product),在線性代數中一般指兩個向量的張量積,其結果為一矩陣;與外積相對,兩向量的內積結果為純量。
外積也可視作是矩陣的克羅內克積的一種特例。注意到:一些作者將「張量的外積」作為張量積的同義詞。
矩陣乘法定義
向量的外積是矩陣的克羅內克積的特殊情況。
給定 ![]() 列向量
列向量 ![]() 和
和 ![]() 行向量
行向量 ![]() ,它們的外積
,它們的外積 ![]() 被定義為
被定義為 ![]() 矩陣
矩陣 ![]() ,結果出自
,結果出自
![]()
這裡的張量積就是向量的乘法。
使用座標:
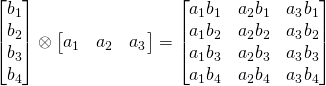
- 如果
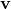 是列向量,定義變為:
是列向量,定義變為: 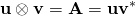
- 這裡的
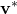 是
是 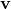
的共軛轉置。
相對於外積
如果 ![]() 是行向量,而且m = n,則可以採用其他方式的積,生成一個純量(或
是行向量,而且m = n,則可以採用其他方式的積,生成一個純量(或 ![]() 矩陣):
矩陣):
![]()
故其『運算子』以通用之 ![]() 表示矣。
表示矣。
雖然,或與『狄拉克標記』僅一步之遙也。
※ 互讀
Vector spaces
Vectors vs kets
In mathematics, the term “vector” is used to refer generally to any element of any vector space. In physics, however, the term “vector” is much more specific: “Vector” refers almost exclusively to quantities like displacement or velocity, which have three components that relate directly to the three dimensions of the real world. Such vectors are typically denoted with over arrows (r→) or boldface (r).
In quantum mechanics, a quantum state is typically represented as an element of an abstract complex vector space—for example the infinite-dimensional vector space of all possible wavefunctions (functions mapping each point of 3D space to a complex number). Since the term “vector” is already used for something else (see previous paragraph), it is very common to refer to these elements of abstract complex vector spaces as “kets”, and to write them using ket notation.
Ket notation
Ket notation, invented by Dirac, uses vertical bars and angular brackets: |A⟩. When this notation is used, these quantities are called “kets”, and |A⟩ is read as “ket-A”.[5] These kets can be manipulated using the usual rules of linear algebra, for example:
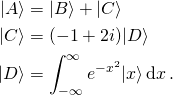
- Note how any symbols, letters, numbers, or even words—whatever serves as a convenient label—can be used as the label inside a ket. For example, the last line above involves infinitely many different kets, one for each real number x. In other words, the symbol “|A⟩” has a specific and universal mathematical meaning, while just the “A” by itself does not. For example, |1⟩ + |2⟩ might or might not be equal to |3⟩. Nevertheless, for convenience, there is usually some logical scheme behind the labels inside kets, such as the common practice of labeling energy eigenkets in quantum mechanics through a listing of their quantum numbers.
Inner products and bras
An inner product is a generalization of the dot product. The inner product of two vectors is a scalar. In neutral notation (notation dedicated to the inner product only), this might be written (A, B), where A and B are elements of the abstract vector space, i.e. both arekets.
Bra–ket notation uses a specific notation for inner products:
![]()
- Bra–ket notation splits this inner product (also called a “bracket”) into two pieces, the “bra” and the “ket”:
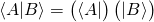
- where ⟨A| is called a bra, read as “bra-A”, and |B⟩ is a ket as above.
The purpose of “splitting” the inner product into a bra and a ket is that both the bra ⟨A| and the ket |B⟩ are meaningful on their own, and can be used in other contexts besides within an inner product. There are two main ways to think about the meanings of separate bras and kets. Accordingly, the interpretation of the expression ⟨A|B⟩ has a second interpretation, namely that of the action of a linear functional per below.
Bras and kets as row and column vectors
For a finite-dimensional vector space, using a fixed orthonormal basis, the inner product can be written as a matrix multiplication of a row vector with a column vector:
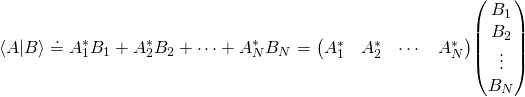
- Based on this, the bras and kets can be defined as:
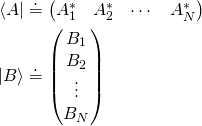
- and then it is understood that a bra next to a ket implies matrix multiplication.
The conjugate transpose (also called Hermitian conjugate) of a bra is the corresponding ket and vice versa:
![]()
- because if one starts with the bra
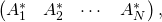
- then performs a complex conjugation, and then a matrix transpose, one ends up with the ket

-
Bras as linear functionals
A more abstract definition, which is equivalent but more easily generalized to infinite-dimensional spaces, is to say that bras are linear functionals on the space of kets, i.e. linear transformations that input a ket and output a complex number. The bra linear functionals are defined to be consistent with the inner product. Thus, if ⟨B| is the linear functional corresponding to |B⟩ under the Riesz representation theorem, then
![]()
- i.e. it produces the same complex number as the inner product does. The terminology for the right hand side is though not inner product, which always involves two kets. Confusing this is harmless, since the same number is produced in the end.
In mathematics terminology, the vector space of bras is the dual space to the vector space of kets, and corresponding bras and kets are related by the Riesz representation theorem.
Non-normalizable states and non-Hilbert spaces
Bra–ket notation can be used even if the vector space is not a Hilbert space.
In quantum mechanics, it is common practice to write down kets which have infinite norm, i.e. non-normalizable wavefunctions. Examples include states whose wavefunctions are Dirac delta functions or infinite plane waves. These do not, technically, belong to theHilbert space itself. However, the definition of “Hilbert space” can be broadened to accommodate these states (see the Gelfand–Naimark–Segal construction or rigged Hilbert spaces). The bra–ket notation continues to work in an analogous way in this broader context.
Banach spaces are a different generalization of Hilbert spaces. In a Banach space B, the vectors may be notated by kets and the continuous linear functionals by bras. Over any vector space without topology, we may also notate the vectors by kets and the linear functionals by bras. In these more general contexts, the bracket does not have the meaning of an inner product, because the Riesz representation theorem does not apply.
原本不宜題外多話,有見於『算符』
Operator (physics)
In physics, an operator is a function over a space[clarification needed] of physical states to another space of physical states. The simplest example of the utility of operators is the study of symmetry (which makes the concept of a group useful in this context). Because of this, they are a very useful tool in classical mechanics. Operators are even more important in quantum mechanics, where they form an intrinsic part of the formulation of the theory.
Operators in classical mechanics
In classical mechanics, the movement of a particle (or system of particles) is completely determined by the Lagrangian ![]() or equivalently the Hamiltonian
or equivalently the Hamiltonian ![]() , a function of the generalized coordinates q, generalized velocities
, a function of the generalized coordinates q, generalized velocities ![]() and its conjugate momenta:
and its conjugate momenta:
![]()
- If either L or H is independent of a generalized coordinate q, meaning the L and H do not change when q is changed, which in turn means the dynamics of the particle are still the same even when q changes, the corresponding momenta conjugate to those coordinates will be conserved (this is part of Noether’s theorem, and the invariance of motion with respect to the coordinate q is a symmetry). Operators in classical mechanics are related to these symmetries.
More technically, when H is invariant under the action of a certain group of transformations G:
![]() .
.
the elements of G are physical operators, which map physical states among themselves.
Table of classical mechanics operators
-
Transformation Operator Position Momentum Translational symmetry 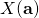
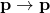
Time translation symmetry 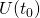
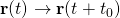
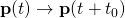
Rotational invariance 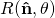
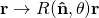
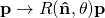
Galilean transformations 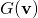
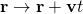
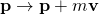
Parity 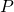
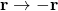
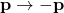
T-symmetry 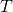
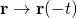
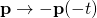
where ![]() is the rotation matrix about an axis defined by the unit vector
is the rotation matrix about an axis defined by the unit vector ![]() and angle θ.
and angle θ.
直觀有利之故,特別假借 Dyadics 範例
Examples
Vector projection and rejection
A nonzero vector a can always be split two perpendicular components, one parallel (‖) to the direction of a unit vector n, and one perpendicular (⊥) to it;
![]()
- The parallel component is found by vector projection, which is equivalent to the dot product of a with the dyadic nn,
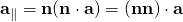
- and the perpendicular component is found from vector rejection, which is equivalent to the dot product of a with the dyadic I − nn,
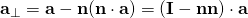
略說一下︰
試問『什麼是一』呢?此『![]() 』在算術『乘法』中滿足
』在算術『乘法』中滿足
![]()
,故因其『乘法恆等性』而特殊也。所以有『單位 □ ○』總總哩!因是所謂『向量』之『單位算符』 ![]() ,不過想說
,不過想說
![]() 而已。
而已。
那麼『平行算符』
![]()
之『意指』能不明白耶?★
豈不得
![]()
的乎?☆
究其實
![]()
,依舊陳述相同理念的呦◎