所謂學問貴在日常生活會活用。能以科學原理之光來解釋周遭所見現象。比方講︰角動量守恆,使滑冰舞者縮腿、臂時轉速增加。

A figure skater conserves angular momentum – her rotational speed increases as her moment of inertia decreases by drawing in her arms and legs.
如斯者將浸蘊於概念內涵,以求深入淺出︰
Angular momentum
Angular momentum in classical mechanics
Definition
Scalar — angular momentum in two dimensions
Velocity of the particle m with respect to the origin O can be resolved into components parallel to (v//) and perpendicular to (v⊥) the radius vectorr. The angular momentum of m is proportional to the perpendicular component v⊥ of the velocity, or equivalently, to the perpendicular distance r⊥ from the origin.
Angular momentum is a vector quantity (more precisely, a pseudovector) that represents the product of a body’s rotational inertia and rotational velocity about a particular axis. However, if the particle’s trajectory lies in a singleplane, it is sufficient to discard the vector nature of angular momentum, and treat it as a scalar (more precisely, a pseudoscalar).[2] Angular momentum can be considered a rotational analog of linear momentum. Thus, where linear momentum ![]() is proportional to mass
is proportional to mass ![]()

![]()

![]()
- angular momentum
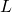 is proportional to moment of inertia
is proportional to moment of inertia 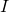 and angular speed
and angular speed 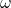 ,[3]
,[3] 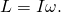
- Unlike mass, which depends only on amount of matter, moment of inertia is also dependent on the position of the axis of rotation and the shape of the matter. Unlike linear speed, which occurs in a straight line, angular speed occurs about a center of rotation. Therefore, strictly speaking,
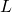 should be referred to as the angular momentum relative to that center.[4]
should be referred to as the angular momentum relative to that center.[4]
Because ![]() for a single particle and
for a single particle and ![]() for circular motion, angular momentum can be expanded,
for circular motion, angular momentum can be expanded, ![]() and reduced to,
and reduced to,
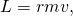
- the product of the radius of rotation
 and the linear momentum of the particle
and the linear momentum of the particle 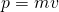 , where
, where  in this case is the equivalent linear (tangential) speed at the radius (
in this case is the equivalent linear (tangential) speed at the radius (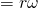 ).
).
This simple analysis can also apply to non-circular motion if only the component of the motion which is perpendicular to the radius vector is considered. In that case,

- where
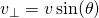 is the perpendicular component of the motion. Expanding,
is the perpendicular component of the motion. Expanding, 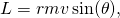 rearranging,
rearranging, 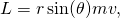 and reducing, angular momentum can also be expressed,
and reducing, angular momentum can also be expressed,
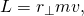
- where
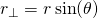 is the length of the moment arm, a line dropped perpendicularly from the origin onto the path of the particle. It is this definition, (length of moment arm)×(linear momentum) to which the term moment of momentum refers.[5]
is the length of the moment arm, a line dropped perpendicularly from the origin onto the path of the particle. It is this definition, (length of moment arm)×(linear momentum) to which the term moment of momentum refers.[5]
Scalar — angular momentum from Lagrangian mechanics
Another approach is to define angular momentum as the conjugate momentum (also called canonical momentum) of the angular coordinate ![]() expressed in the Lagrangian of the mechanical system. Consider a mechanical system with a mass
expressed in the Lagrangian of the mechanical system. Consider a mechanical system with a mass ![]() constrained to move in a circle of radius
constrained to move in a circle of radius ![]() in the absence of any external force field. The kinetic energy of the system is
in the absence of any external force field. The kinetic energy of the system is
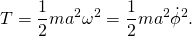
- And the potential energy is
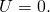
- Then the Lagrangian is
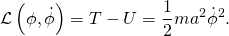
- The generalized momentum “canonically conjugate to” the coordinate
 is defined by
is defined by
-
Vector — angular momentum in three dimensions
To completely define angular momentum in three dimensions, it is required to know the angle swept out in unit time, the direction perpendicular to the instantaneous plane of angular displacement, and the sense (right- or left-handed) of the angular velocity, as well as the mass involved.[6] By retaining this vector nature of angular momentum, the general nature of the equations is also retained, and can describe any sort of three-dimensional motionabout the center of rotation – circular, linear, or otherwise. In vector notation, the angular momentum of a point particle in motion about the origin is defined as:
![]() where
where
![]() is the moment of inertia for a point mass,
is the moment of inertia for a point mass,
-
 is the angular velocity of the particle about the origin,
is the angular velocity of the particle about the origin,
-
 is the position vector of the particle relative to the origin,
is the position vector of the particle relative to the origin,  ,
,
-
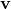 is the linear velocity of the particle relative to the origin,
is the linear velocity of the particle relative to the origin,
-
- and
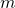 is the mass of the particle.
is the mass of the particle.
- and
This can be expanded, ![]() reduced,
reduced, ![]() and by the rules of vector algebra rearranged to the form,
and by the rules of vector algebra rearranged to the form,
![]()
- which is the cross product of the position vector
 and the linear momentum
and the linear momentum 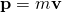 of the particle. By the definition of the cross product, the
of the particle. By the definition of the cross product, the 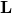 vector is perpendicular to both
vector is perpendicular to both  and
and 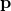 . It is directed perpendicular to the plane of angular displacement, as indicated by the right-hand rule – so that the angular velocity is seen as counter-clockwise from the head of the vector. Conversely, the
. It is directed perpendicular to the plane of angular displacement, as indicated by the right-hand rule – so that the angular velocity is seen as counter-clockwise from the head of the vector. Conversely, the 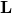 vector defines the plane in which
vector defines the plane in which  and
and 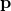 lie.
lie.
By defining a unit vector ![]() perpendicular to the plane of angular displacement, a scalar angular speed
perpendicular to the plane of angular displacement, a scalar angular speed ![]() results, where
results, where
![]() and
and
![]() where
where ![]() is the perpendicular component of the motion, as above.
is the perpendicular component of the motion, as above.
The two-dimensional scalar equations of the previous section can thus be given direction:
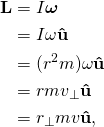
- and
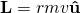 for circular motion, where all of the motion is perpendicular to the radius
for circular motion, where all of the motion is perpendicular to the radius 
.
進而可觸類旁通也◎
Example: The banked turn
The upper panel in the image at right shows a ball in circular motion on a banked curve. The curve is banked at an angle θ from the horizontal, and the surface of the road is considered to be slippery. The objective is to find what angle the bank must have so the ball does not slide off the road.[11] Intuition tells us that, on a flat curve with no banking at all, the ball will simply slide off the road; while with a very steep banking, the ball will slide to the center unless it travels the curve rapidly.
Apart from any acceleration that might occur in the direction of the path, the lower panel of the image above indicates the forces on the ball. There are two forces; one is the force of gravity vertically downward through the center of mass of the ball mg, where m is the mass of the ball and g is the gravitational acceleration; the second is the upward normal force exerted by the road at a right angle to the road surface man. The centripetal force demanded by the curved motion is also shown above. This centripetal force is not a third force applied to the ball, but rather must be provided by the net force on the ball resulting from vector addition of the normal force and the force of gravity. The resultant or net force on the ball found by vector addition of the normal force exerted by the road and vertical force due to gravity must equal the centripetal force dictated by the need to travel a circular path. The curved motion is maintained so long as this net force provides the centripetal force requisite to the motion.
The horizontal net force on the ball is the horizontal component of the force from the road, which has magnitude |Fh| = m|an|sinθ. The vertical component of the force from the road must counteract the gravitational force: |Fv| =m|an|cosθ = m|g|, which implies |an|=|g| / cosθ. Substituting into the above formula for |Fh| yields a horizontal force to be:
![]()
- On the other hand, at velocity |v| on a circular path of radius r, kinematics says that the force needed to turn the ball continuously into the turn is the radially inward centripetal force Fc of magnitude:
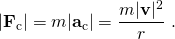
- Consequently, the ball is in a stable path when the angle of the road is set to satisfy the condition:
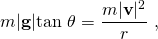
- or,
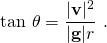
As the angle of bank θ approaches 90°, the tangent function approaches infinity, allowing larger values for |v|2/r. In words, this equation states that for faster speeds (bigger |v|) the road must be banked more steeply (a larger value for θ), and for sharper turns (smaller r) the road also must be banked more steeply, which accords with intuition. When the angle θ does not satisfy the above condition, the horizontal component of force exerted by the road does not provide the correct centripetal force, and an additional frictional force tangential to the road surface is called upon to provide the difference. If friction cannot do this (that is, the coefficient of friction is exceeded), the ball slides to a different radius where the balance can be realized.[12][13]
These ideas apply to air flight as well. See the FAA pilot’s manual.[14]


