那麼科學上如何看待『預言』的呢?比方講一七四四年瑞士大數學家和物理學家萊昂哈德‧歐拉 Leonhard Euler 在《尋找具有極大值或極小值性質的曲線,等周問題的最廣義解答》 Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes, sive solutio problematis isoperimetrici lattissimo sensu accepti 論文中,非常清晰明白的給出『最小作用量原理』的定義
假使一個質量為 ![]() ,速度為
,速度為 ![]() 的粒子移動無窮小距離
的粒子移動無窮小距離 ![]() 時。這時粒子的動量為
時。這時粒子的動量為 ![]() ,當乘以此無窮小距離
,當乘以此無窮小距離 ![]() 後,給出
後,給出 ![]() ,這是粒子的動量作用於無窮小『路徑』
,這是粒子的動量作用於無窮小『路徑』 ![]() 距離之上。我宣稱︰在所有連結『始終』兩個端點的可能『路徑』之中,這個粒子運動的真實『軌跡』是
距離之上。我宣稱︰在所有連結『始終』兩個端點的可能『路徑』之中,這個粒子運動的真實『軌跡』是 ![]() 為最小值的『路徑』;如果假定質量是個常數,也就是
為最小值的『路徑』;如果假定質量是個常數,也就是![]() 為最小值的『軌道』。
為最小值的『軌道』。
也就是說,在所有連結『始終』兩個端點的可能『路徑』![]() 之中, 粒子所選擇的『路徑』是『作用量』
之中, 粒子所選擇的『路徑』是『作用量』![]() 泛函數的『極值』,這是牛頓第二運動定律的『變分法』Variation 描述。如果從今天物理能量的觀點來看
泛函數的『極值』,這是牛頓第二運動定律的『變分法』Variation 描述。如果從今天物理能量的觀點來看 ![]() ,此處
,此處 ![]() 就是粒子的動能。因為牛頓第二運動定律可以表述為
就是粒子的動能。因為牛頓第二運動定律可以表述為 ![]() ,所以
,所以 ![]() 。
。
假使粒子所受的力是『保守力』conservative force,也就是講此力沿著任何路徑所作的『功』work 只跟粒子『始終』兩個端點的『位置』有關,與它行經的『路徑』無關。在物理上這時通常將它定義成這個『力場』的『位能』![]() ,於是如果一個粒子在一個保守場中,
,於是如果一個粒子在一個保守場中,![]() ,這就是物理上『能量守恆』原理!舉例來說重力、彈簧力、電場力等等,都是保守力,然而摩擦力和空氣阻力種種都是典型的非保守力。由於
,這就是物理上『能量守恆』原理!舉例來說重力、彈簧力、電場力等等,都是保守力,然而摩擦力和空氣阻力種種都是典型的非保守力。由於 ![]() 在這些可能路徑裡都不變,因此『最小作用量原理』所確定的『路徑』也就是『作用量』
在這些可能路徑裡都不變,因此『最小作用量原理』所確定的『路徑』也就是『作用量』 ![]() 的『極值』。一七八八年法國籍義大利裔數學家和天文學家約瑟夫‧拉格朗日 Joseph Lagrange 對於變分法發展貢獻很大,最早在其論文《分析力學》Mecanique Analytique 裡,使用『能量守恆定律』推導出了歐拉陳述的最小作用量原理的正確性。
的『極值』。一七八八年法國籍義大利裔數學家和天文學家約瑟夫‧拉格朗日 Joseph Lagrange 對於變分法發展貢獻很大,最早在其論文《分析力學》Mecanique Analytique 裡,使用『能量守恆定律』推導出了歐拉陳述的最小作用量原理的正確性。
從數學上講運動的『微分方程式』等效於對應的『積分方程式』 ,這本不是什麼奇怪的事,當人們開始考察它的『哲學意義』,可就引發很多不同的觀點。有人說 ![]() 就像『結果
就像『結果 ![]() 原因』描繪『因果』的『瞬刻聯繫』關係,這是一種『決定論』,從一個『時空點』推及『無窮小時距』
原因』描繪『因果』的『瞬刻聯繫』關係,這是一種『決定論』,從一個『時空點』推及『無窮小時距』 ![]() 接續的另一個『時空點』,因此一旦知道『初始狀態』,就已經確定了它的『最終結局』!有人講
接續的另一個『時空點』,因此一旦知道『初始狀態』,就已經確定了它的『最終結局』!有人講 ![]() 彷彿確定了『目的地』無論從哪個『起始處』出發,總會有一個『通達路徑』,這成了一種『目的論』,大自然自會找到『此時此處』通向『彼時彼處』的『道路』!!各種意義『詮釋』果真耶?宛如說『花開自有因,將要為誰妍』??
彷彿確定了『目的地』無論從哪個『起始處』出發,總會有一個『通達路徑』,這成了一種『目的論』,大自然自會找到『此時此處』通向『彼時彼處』的『道路』!!各種意義『詮釋』果真耶?宛如說『花開自有因,將要為誰妍』??
所謂『科學的預言』不過是依據『條件』應用『自然律』所得到的『邏輯結論』罷了!設使『條件』正確,『定律』無誤,『推演』合理,若說『結果』不發生,怕也是『不可能』的了!也許本就不該有『環保問題』,因為對於孕育『人類生命』的『地球』理當懷著『謝天』的情懷,自然應該『愛惜保護』自己棲息的『大地』。並非是一再問著已經『氣候變遷』了嗎?或祇是不怕不悔,就怕是悔之晚矣!!
─── 《踏雪尋梅!!》
如果說牛頓力學已經『完備』,為什麼要追求『等效』描述呢?
一則可藉之深入了解『運動定律』的邏輯蘊含,發現深藏不易見核心『物理概念』!比方說『能量守恆定律』︰
拉格朗日的表述
約瑟夫·拉格朗日對於變分法貢獻良多。拉格朗日在論文《分析力學》(Mecanique Analytique)裏,從能量守恆定律理論推導出歐拉表述的最小作用量原理是正確的[4]。能量守恆定律以方程式表達為
![]() ;
;
位能的變分為
![]() ;
;
其中,![]() 是粒子的位置,
是粒子的位置,![]() 是虛位移。
是虛位移。
粒子感受到的作用力 ![]() 為位能的負梯度。將牛頓第二定律帶入方程式,
為位能的負梯度。將牛頓第二定律帶入方程式,
![]() 。
。
微分運算可以和變分運算對易:
![]() ;
;
其中,![]() 是粒子的速度。
是粒子的速度。
所以,位能的變分為
![]() 。
。
動能的變分為
![]() 。
。
總能量的變分為:
![]() ;
;
總能量的積分的變分為
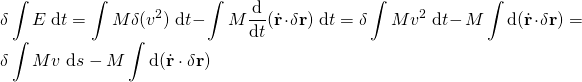 ;
;
其中,![]() 是路徑長度。
是路徑長度。
設定路徑的兩個端點為固定不變,能量也守恆不變,則粒子移動的路徑的作用量是穩定值:
![]() 。
。
拉格朗日最小作用量原理
推廣至位形空間,拉格朗日最小作用量原理闡明,
![]() ;
;
歐拉-拉格朗日最小作用量原理
拉格朗日又注意到在作用量的方程式 ![]() 中,
中,
![]() 。
。
將這方程式代入作用量,可以看見被積分項目是動能項目:
![]() 。
。
因此,作用量也可以表達為(忽略常數乘法因子)
![]() 。
。
歐拉-拉格朗日最小作用量原理表明,描述粒子運動的作用量必定是穩定值[13]:
![]() 。
。
請特別注意,這方程式看起來簡易精緻,然而,隱藏在使用方面有很大的問題。歐拉的作用量積分於路徑;而這作用量積分於時間。變分法要求積分域兩端固定不變。雖然路徑兩端是固定值,轉換至時間,為了要滿足能量守恆,時間間隔的兩端可能不是固定值。亞可比因此批評拉格朗日的方法有瑕疵[13]。後來,於1816年,奧淩迪·若立格(Olinde Rodrigues)想出新點子,將這時間作用量的變分詳細計算出來[1]。
實乃拉格朗日功績之一也。
更重要的是不同自然原理『形式』更能開拓視野啟迪來者啊◎
Further development
Euler continued to write on the topic; in his Reflexions sur quelques loix generales de la nature (1748), he called the quantity “effort”. His expression corresponds to what we would now call potential energy, so that his statement of least action in statics is equivalent to the principle that a system of bodies at rest will adopt a configuration that minimizes total potential energy.
Lagrange and Hamilton
Much of the calculus of variations was stated by Joseph-Louis Lagrange in 1760[25][26] and he proceeded to apply this to problems in dynamics. In Méchanique Analytique (1788) Lagrange derived the general equations of motion of a mechanical body.[27] William Rowan Hamilton in 1834 and 1835[28] applied the variational principle to the classical Lagrangian function
![]()
- to obtain the Euler–Lagrange equations in their present form.
Jacobi and Morse
In 1842, Carl Gustav Jacobi tackled the problem of whether the variational principle always found minima as opposed to other stationary points (maxima or stationary saddle points); most of his work focused on geodesics on two-dimensional surfaces.[29] The first clear general statements were given by Marston Morse in the 1920s and 1930s,[30] leading to what is now known as Morse theory. For example, Morse showed that the number of conjugate points in a trajectory equalled the number of negative eigenvalues in the second variation of the Lagrangian.
Gauss and Hertz
Other extremal principles of classical mechanics have been formulated, such as Gauss’s principle of least constraint and its corollary, Hertz’s principle of least curvature.
然有所得者,或有所失夫!!
The classical Lagrangian function
![]()
恐不易概括『耗散力』乎??
Advanced Classical Mechanics/Dissipative Forces
Dissipative forces are forces of such nature that energy is lost from a system when motion takes place. Of course energy is in general conserved but it is lost from the degrees of freedom of interest into heat (the random motion of internal degrees of freedom) or radiation (the motion of new particles created by the motion — light usually).
The force can often be represented by ![]() Depending on the value of the index
Depending on the value of the index ![]() we have different types of dissipative forces.
we have different types of dissipative forces.
………
故須小心『 □ □ 原理』說法裡,未言而請自明『假設』呦◎
將可咀嚼『虛功』之『橄欖味』矣!!??
Virtual work
Virtual work arises in the application of the principle of least action to the study of forces and movement of a mechanical system. The work of a force acting on a particle as it moves along a displacement will be different for different displacements. Among all the possible displacements that a particle may follow, called virtual displacements, one will minimize the action. This displacement is therefore the displacement followed by the particle according to the principle of least action. The work of a force on a particle along a virtual displacement is known as the virtual work.
Historically, virtual work and the associated calculus of variations were formulated to analyze systems of rigid bodies,[1] but they have also been developed for the study of the mechanics of deformable bodies.[2]
Introduction
Consider a particle P that moves from a point A to a point B along a trajectory r(t), while a force F(r(t)) is applied to it. The work done by the force F is given by the integral
![]()
- where dr is the differential element along the curve that is the trajectory of P, and v is its velocity. It is important to notice that the value of the work W depends on the trajectory r(t).
Now consider particle P that moves from point A to point B again, but this time it moves along the nearby trajectory that differs from r(t) by the variation δr(t)=εh(t), where ε is a scaling constant that can be made as small as desired and h(t) is an arbitrary function that satisfies h(t0) = h(t1) = 0. Suppose the force F(r(t)+εh(t)) is the same as F(r(t)). The work done by the force is given by the integral
![]()
- The variation of the work δW associated with this nearby path, known as the virtual work, can be computed to be
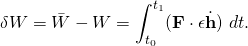
- If there is no constraint force, then 6 parameters are needed to completely describe the motion of P. If there are k (k ≤ 6) constraint forces, then n = (6 – k) parameters are needed. Hence, we can define n generalized coordinates qi (t) (i = 1, 2, …, n), and express r(t) and δr=εh(t) in terms of the generalized coordinates. That is,
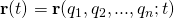 ,
,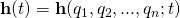 .
.
Then, the derivative of the variation δr=εh(t) is given by
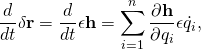
- then we have
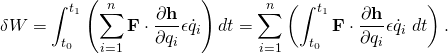
- The requirement that the virtual work be zero for an arbitrary variation δr(t)=εh(t) is equivalent to the set of requirements
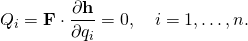
- The terms Qi are called the generalized forces associated with the virtual displacement δr.
Static equilibrium
Static equilibrium is a state in which the net force and net torque acted upon the system is zero. In other words, both linear momentum and angular momentum of the system are conserved. The principle of virtual work states that the virtual work of the applied forces is zero for all virtual movements of the system from static equilibrium. This principle can be generalised such that three dimensional rotations are included: the virtual work of the applied forces and applied moments is zero for all virtual movements of the system from static equilibrium. That is
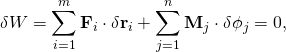
- where Fi , i = 1, 2, …, m and Mj , j = 1, 2, …, n are the applied forces and applied moments, respectively, and δri , i = 1, 2, …, m and δφj , j = 1, 2, …, n are the virtual displacements and virtual rotations, respectively.
Suppose the system consists of N particles, and it has f (f ≤ 6N) degrees of freedom. It is sufficient to use only f coordinates to give a complete description of the motion of the system, so f generalised coordinates qk , k = 1, 2, …, f are defined such that the virtual movements can be expressed in terms of these generalised coordinates. That is,
![]()
![]()
- The virtual work can then be reparametrised by the generalised coordinates:
![Rendered by QuickLaTeX.com \displaystyle \delta W=\sum _{k=1}^{f}\left[\left(\sum _{i=1}^{m}\mathbf {F} _{i}\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{k}}}+\sum _{j=1}^{n}\mathbf {M} _{j}\cdot {\frac {\partial \mathbf {\phi } _{j}}{\partial q_{k}}}\right)\delta q_{k}\right]=\sum _{k=1}^{f}Q_{k}\delta q_{k},](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-946a069b21fa13ba4597f6ecf7a08a41_l3.png)
- where the generalised forces Qk are defined as
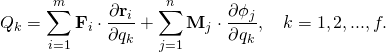
- Kane[5] shows that these generalised forces can also be formulated in terms of the ratio of time derivatives. That is,
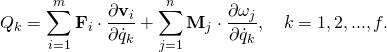
- The principle of virtual work requires that the virtual work done on a system by the forces Fi and moments Mj vanishes if it is in equilibrium. Therefore, the generalized forces Qk are zero, that is
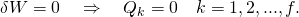
-
Constraint forces
An important benefit of the principle of virtual work is that only forces that do work as the system moves through a virtual displacement are needed to determine the mechanics of the system. There are many forces in a mechanical system that do no work during avirtual displacement, which means that they need not be considered in this analysis. The two important examples are (i) the internal forces in a rigid body, and (ii) the constraint forces at an ideal joint.
Lanczos[1] presents this as the postulate: “The virtual work of the forces of reaction is always zero for any virtual displacement which is in harmony with the given kinematic constraints.” The argument is as follows. The principle of virtual work states that in equilibriumthe virtual work of the forces applied to a system is zero. Newton’s laws state that at equilibrium the applied forces are equal and opposite to the reaction, or constraint forces. This means the virtual work of the constraint forces must be zero as well.
Law of the lever
A lever is modeled as a rigid bar connected to a ground frame by a hinged joint called a fulcrum. The lever is operated by applying an input force FA at a point A located by the coordinate vector rA on the bar. The lever then exerts an output force FB at the point Blocated by rB. The rotation of the lever about the fulcrum P is defined by the rotation angle θ.
Let the coordinate vector of the point P that defines the fulcrum be rP, and introduce the lengths
![]()
- which are the distances from the fulcrum to the input point A and to the output point B, respectively.
Now introduce the unit vectors eA and eB from the fulcrum to the point A and B, so
![]()
- This notation allows us to define the velocity of the points A and B as

- where eA⊥ and eB⊥ are unit vectors perpendicular to eA and eB, respectively.
The angle θ is the generalized coordinate that defines the configuration of the lever, therefore using the formula above for forces applied to a one degree-of-freedom mechanism, the generalized force is given by
![]()
- Now, denote as FA and FB the components of the forces that are perpendicular to the radial segments PA and PB. These forces are given by
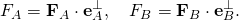
- This notation and the principle of virtual work yield the formula for the generalized force as
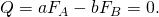
- The ratio of the output force FB to the input force FA is the mechanical advantage of the lever, and is obtained from the principle of virtual work as
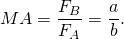
- This equation shows that if the distance a from the fulcrum to the point A where the input force is applied is greater than the distance b from fulcrum to the point B where the output force is applied, then the lever amplifies the input force. If the opposite is true that the distance from the fulcrum to the input point A is less than from the fulcrum to the output point B, then the lever reduces the magnitude of the input force.
This is the law of the lever, which was proven by Archimedes using geometric reasoning.[6]
