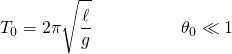在進入

pydy-tutorial-human-standing

筆記第三章

Introduction

The first step, and notably the most difficult, is to define the kinematic relationships (i.e. motion) among rigid bodies in the system. Here will we make use of ReferenceFrameobjects to describe the four frames in the problem, set their orientations, and then construct vectors in the frames that position various important Points. Finally, we will specify the linear and angular velocities of the frames and points using generalized speeds.

……

之前，讓我們且藉若干篇幅詳細解說『單擺』範例︰

Nonminimal Coordinates Pendulum

In this example we demonstrate the use of the functionality provided in mechanics for deriving the equations of motion (EOM) for a pendulum with a nonminimal set of coordinates. As the pendulum is a one degree of freedom system, it can be described using one coordinate and one speed (the pendulum angle, and the angular velocity respectively). Choosing instead to describe the system using the $x$ and $y$ coordinates of the mass results in a need for constraints. The system is shown below:

The system will be modeled using both Kane’s and Lagrange’s methods, and the resulting EOM linearized. While this is a simple problem, it should illustrate the use of the linearization methods in the presence of constraints.

暨能了解 SymPy mechanics 文件筆法以及符號習慣也！比方說

Lagrange’s Method in Physics/Mechanics

mechanics provides functionality for deriving equations of motion using Lagrange’s method. This document will describe Lagrange’s method as used in this module, but not how the equations are actually derived.

之

Structure of Equations

In mechanics we are assuming there are 3 basic sets of equations needed to describe a system; the constraint equations, the time differentiated constraint equations and the dynamic equations.

$\mathbf{m_{c}}(q, t) \dot{q} + \mathbf{f_{c}}(q, t) = 0$

$\mathbf{m_{dc}}(\dot{q}, q, t) \ddot{q} + \mathbf{f_{dc}}(\dot{q}, q, t) &= 0$

$\mathbf{m_d}(\dot{q}, q, t) \ddot{q} + \mathbf{\Lambda_c}(q, t)\lambda + \mathbf{f_d}(\dot{q}, q, t) = 0$

In this module, the expressions formed by using Lagrange’s equations of the second kind are rearranged into the following form:

$\mathbf{M}(q, t) x = \mathbf{f}(q, \dot{q}, t)$

where in the case of a system without constraints:

$x = \ddot{q}$

For a constrained system with $n$ generalized speeds and $m$ constraints, we will get n – m equations. The mass-matrix/forcing equations are then augmented in the following fashion:

$x = \begin{bmatrix} \ddot{q} \\ \lambda \end{bmatrix}$

$\mathbf{M}(q, t) = \begin{bmatrix} \mathbf{m_d}(q, t) & \mathbf{\Lambda_c}(q, t) \end{bmatrix}$

$\mathbf{F}(\dot{q}, q, t) = \begin{bmatrix} \mathbf{f_d}(q, \dot{q}, t) \end{bmatrix}$

裡的

‧ $q$ 代表廣義座標

‧ $t$ 代表時間

‧ $\dot{q}$ 是廣義速度 $= \frac{d}{dt} q$

‧ $\ddot{q}$ 指廣義加速度 $= \frac{d}{dt} \dot{q}$

‧ 足標 $\mathbf{f}_c (q, t)$ 之 $c$ 是『約束』constraint 之縮寫

‧ 足標 $\mathbf{f}_{d} (\dot{q},q, t)$ 之 $d$ 是『動力』 dynamic 的縮寫。

‧ $\lambda$ 是 Lagrange multiplier

‧ ………

皆用『 □ ○形式』描述『允許型態』也。熟悉拉格朗日力學的人或容易揣想乎？也可為尚未學習 Kane 法者之鑑耶？？

其次，讀者不要認為『單擺』簡單呦！！

Pendulum (mathematics)

The mathematics of pendulums are in general quite complicated. Simplifying assumptions can be made, which in the case of a simple pendulum allow the equations of motion to be solved analytically for small-angle oscillations.

幾經『假設』，

Simple gravity pendulum

Animation of a pendulum showing the velocity and acceleration vectors.

A so-called “simple pendulum” is an idealization of a “real pendulum” but in an isolated system using the following assumptions:

The rod or cord on which the bob swings is massless, inextensible and always remains taut;
The bob is a point mass;
Motion occurs only in two dimensions, i.e. the bob does not trace an ellipse but an arc.
The motion does not lose energy to friction or air resistance.
The gravitational field is uniform.
The support does not move.

The differential equation which represents the motion of a simple pendulum is

$\displaystyle {\frac {d^{2}\theta }{dt^{2}}}+{\frac {g}{\ell }}\sin \theta =0$ Eq. 1

where $g$ is acceleration due to gravity, $l$ is the length of the pendulum, and $θ$ is the angular displacement.

※ 參讀

“Energy” derivation of (Eq. 1)

Figure 2. Trigonometry of a simple gravity pendulum.

It can also be obtained via the conservation of mechanical energy principle: any object falling a vertical distance $\displaystyle h$ would acquire kinetic energy equal to that which it lost to the fall. In other words, gravitational potential energy is converted into kinetic energy. Change in potential energy is given by

$\displaystyle \Delta U=mgh.\,$

The change in kinetic energy (body started from rest) is given by

$\displaystyle \Delta K={\tfrac {1}{2}}mv^{2}.$

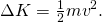
Since no energy is lost, the gain in one must be equal to the loss in the other

$\displaystyle {\tfrac {1}{2}}mv^{2}=mgh.\,$

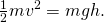
The change in velocity for a given change in height can be expressed as

$\displaystyle v={\sqrt {2gh}}.\,$

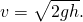
Using the arc length formula above, this equation can be rewritten in terms of

dθ / dt

$\displaystyle {\begin{aligned}v=\ell {\frac {d\theta }{dt}}&={\sqrt {2gh}},\quad {\text{so}}\\{\frac {d\theta }{dt}}&={\frac {\sqrt {2gh}}{l}},\end{aligned}}$

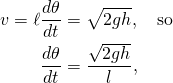
where

h

is the vertical distance the pendulum fell. Look at Figure 2, which presents the trigonometry of a simple pendulum. If the pendulum starts its swing from some initial angle

θ 0

, then

y 0

, the vertical distance from the screw, is given by

$\displaystyle y_{0}=\ell \cos \theta _{0}.\,$

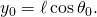
Similarly, for

y 1

, we have

$\displaystyle y_{1}=\ell \cos \theta .\,$

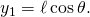
Then

h

is the difference of the two

$\displaystyle h=\ell \left(\cos \theta -\cos \theta _{0}\right).$

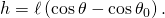
In terms of

dθ / dt

gives

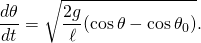$\displaystyle {\frac {d\theta }{dt}}={\sqrt {{\frac {2g}{\ell }}(\cos \theta -\cos \theta _{0})}}.$ Eq. 2

This equation is known as the first integral of motion, it gives the velocity in terms of the location and includes an integration constant related to the initial displacement ( $θ 0$ ). We can differentiate, by applying the chain rule, with respect to time to get the acceleration

$\displaystyle {\begin{aligned}{\frac {d}{dt}}{\frac {d\theta }{dt}}&={\frac {d}{dt}}{\sqrt {{\frac {2g}{\ell }}\left(\cos \theta -\cos \theta _{0}\right)}},\\{\frac {d^{2}\theta }{dt^{2}}}&={\frac {1}{2}}{\frac {-{\frac {2g}{\ell }}\sin \theta }{\sqrt {{\frac {2g}{\ell }}(\cos \theta -\cos \theta _{0})}}}{\frac {d\theta }{dt}}\\&={\frac {1}{2}}{\frac {-{\frac {2g}{\ell }}\sin \theta }{\sqrt {{\frac {2g}{\ell }}(\cos \theta -\cos \theta _{0})}}}{\sqrt {{\frac {2g}{\ell }}(\cos \theta -\cos \theta _{0})}}=-{\frac {g}{\ell }}\sin \theta ,\\{\frac {d^{2}\theta }{dt^{2}}}&+{\frac {g}{\ell }}\sin \theta =0,\end{aligned}}$

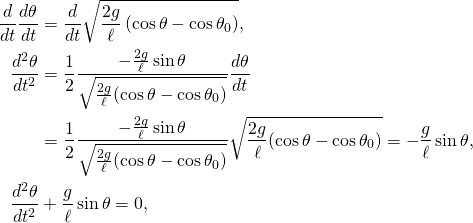
which is the same result as obtained through force analysis.

依舊難以『解析』，故有『小角度近似』

Small-angle approximation

Small-angle approximation for the sine function: For

θ \approx 0

we find

sin θ \approx θ

The differential equation given above is not easily solved, and there is no solution that can be written in terms of elementary functions. However adding a restriction to the size of the oscillation’s amplitude gives a form whose solution can be easily obtained. If it is assumed that the angle is much less than 1 radian (often cited as less than 0.1 radians, about 6°), or

$\displaystyle \theta \ll 1,\,$

then substituting for

sin θ

into Eq. 1 using the small-angle approximation,

$\displaystyle \sin \theta \approx \theta ,\,$

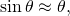
yields the equation for a harmonic oscillator,

$\displaystyle {\frac {d^{2}\theta }{dt^{2}}}+{\frac {g}{\ell }}\theta =0.$

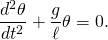
The error due to the approximation is of order

θ 3

(from the Maclaurin series for

sin θ

Given the initial conditions $θ (0) = θ 0$ and $dθ / dt (0) = 0$ , the solution becomes

$\displaystyle \theta (t)=\theta _{0}\cos \left({\sqrt {\frac {g}{\ell }}}\,t\right)\quad \quad \quad \quad \theta _{0}\ll 1.$

The motion is simple harmonic motion where $θ 0$ is the amplitude of the oscillation (that is, the maximum angle between the rod of the pendulum and the vertical). The period of the motion, the time for a complete oscillation (outward and return) is

$\displaystyle T_{0}=2\pi {\sqrt {\frac {\ell }{g}}}\quad \quad \quad \quad \quad \theta _{0}\ll 1$

which is known as Christiaan Huygens‘s law for the period. Note that under the small-angle approximation, the period is independent of the amplitude $θ 0$ ; this is the property of isochronism that Galileo discovered.

，『線性化』舉措哩？？！！

早為『數值分析』打開大門矣！！？？

Arbitrary-amplitude period

Figure 3. Deviation of the “true” period of a pendulum from the small-angle approximation of the period. “True” value was obtained numerically evaluating the elliptic integral.

Figure 4. Relative errors using the power series for the period.

Figure 5. Potential energy and phase portrait of a simple pendulum. Note that the

x

-axis, being angle, wraps onto itself after every 2

π

radians.

For amplitudes beyond the small angle approximation, one can compute the exact period by first inverting the equation for the angular velocity obtained from the energy method (Eq. 2),

$\displaystyle {\frac {dt}{d\theta }}={\sqrt {\frac {\ell }{2g}}}{\frac {1}{\sqrt {\cos \theta -\cos \theta _{0}}}}$

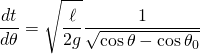
and then integrating over one complete cycle,

$\displaystyle T=t(\theta _{0}\rightarrow 0\rightarrow -\theta _{0}\rightarrow 0\rightarrow \theta _{0}),$

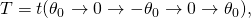
or twice the half-cycle

$\displaystyle T=2t(\theta _{0}\rightarrow 0\rightarrow -\theta _{0}),$

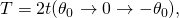
or four times the quarter-cycle

$\displaystyle T=4t(\theta _{0}\rightarrow 0),$

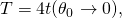
which leads to

$\displaystyle T=4{\sqrt {\frac {\ell }{2g}}}\int _{0}^{\theta _{0}}{\frac {1}{\sqrt {\cos \theta -\cos \theta _{0}}}}\,d\theta .$

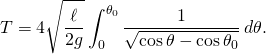
Note that this integral diverges as

θ 0

approaches the vertical

$\displaystyle \lim _{\theta _{0}\rightarrow \pi }T=\infty ,$

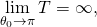
so that a pendulum with just the right energy to go vertical will never actually get there. (Conversely, a pendulum close to its maximum can take an arbitrarily long time to fall down.)

This integral can be rewritten in terms of elliptic integrals as

$\displaystyle T=4{\sqrt {\frac {\ell }{g}}}F\left({\frac {\pi }{2}},\sin {\frac {\theta _{0}}{2}}\right)$

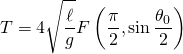
where

F

is the incomplete elliptic integral of the first kind defined by

$\displaystyle F(\varphi ,k)=\int _{0}^{\varphi }{\frac {1}{\sqrt {1-k^{2}\sin ^{2}u}}}\,du\,.$

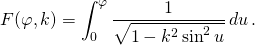
Or more concisely by the substitution

$\displaystyle \sin {u}={\frac {\sin {\frac {\theta }{2}}}{\sin {\frac {\theta _{0}}{2}}}}$

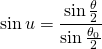
expressing

θ

in terms of

u

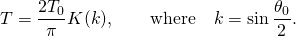$\displaystyle T={\frac {2T_{0}}{\pi }}K(k),\qquad \mathrm {where} \quad k=\sin {\frac {\theta _{0}}{2}}.$ Eq. 3

Here $K$ is the complete elliptic integral of the first kind defined by

$\displaystyle K(k)=F\left({\frac {\pi }{2}},k\right)=\int _{0}^{\frac {\pi }{2}}{\frac {1}{\sqrt {1-k^{2}\sin ^{2}u}}}\,du\,.$

For comparison of the approximation to the full solution, consider the period of a pendulum of length 1 m on Earth (

g

= 9.80665 m/s²) at initial angle 10 degrees is

$\displaystyle 4{\sqrt {\frac {1{\text{ m}}}{g}}}\ K\left(\sin {\frac {10^{\circ }}{2}}\right)\approx 2.0102{\text{ s}}.$

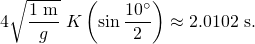
The linear approximation gives

$\displaystyle 2\pi {\sqrt {\frac {1{\text{ m}}}{g}}}\approx 2.0064{\text{ s}}.$

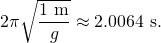
The difference between the two values, less than 0.2%, is much less than that caused by the variation of

g

with geographical location.

日	一	二	三	四	五	六
« 3 月				5 月 »
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30

FreeSandal

每日彙整: 2018-04-17

STEM 隨筆︰古典力學︰運動學【四】