伽利略、克卜勒與潮汐理論
紅衣主教貝拉明[48]1615年發表聲明,稱哥白尼學說不成立,除非「有物理證據證明太陽不是圍繞地球,而是地球圍繞著太陽運行 」[49]。伽利略認為他的潮汐理論足可證明地球運動。這個理論十分重要,以至於他最開始將著作命名為《關于海洋潮汐與流動的兩大世界體系的對話》[50]。關於潮汐的字眼最終因為宗教法庭的指令而被刪除。
伽利略認為,由於地球圍繞軸心自轉並圍繞太陽公轉,導致地球表面運動的加速減速引發海水潮汐式前後涌動。1616年,他將第一份有關潮汐的文獻整理出來,交給了紅衣主教奧斯尼[51][52]。他的理論第一次涉及了海底大陸架的形狀尺度,以及潮汐的時刻等 。例如,他正確地推算出亞德里亞海中途的波浪相對於到達海岸的最後一波來說可以忽略不計。但是,從潮汐形成的總體角度來看,伽利略的理論並不成立。
如果理論成立了,那麼每天只能出現一次漲潮。伽利略與他的同事們注意到該理論的不足之處,因為在威尼斯每天會漲潮兩次,時間間隔為12小時。伽利略認為這種反常現象不過是因為海洋形狀,深度及其它的問題導致的[53],不值得一提。對於他這種觀點是不可信賴的論斷,阿爾伯特·愛因斯坦則表示伽利略只是急於給出地球運動的物理證明,構造出了這種「引人入勝的觀點」並自己全盤接受了[54]。伽利略否定了當時約翰內斯·克卜勒的觀點,即月球導致潮汐運動[55],而後者的觀點襲承了托勒密法之書中占星傳統。他也拒絕接受克卜勒關於行星沿橢圓軌道運行的觀點,認為圓形軌道才是「完美」的[56]。
─── 摘自《伽利略·伽利萊》
閱讀
潮汐
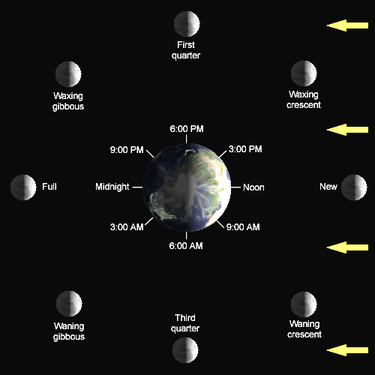
潮汐是地球上的海洋表面受到太陽和月球的萬有引力(潮汐力)作用引起的漲落現象[1][2][3]。潮汐的變化與地球、太陽和月球的相對位置有關,並且會與地球自轉的效應耦合和海洋的海水深度、大湖及河口[4]。在其它引力場的時間和空間系統內也會發生類似潮汐的現象。
在淺海和港灣實際發生的海平面變化,不僅受到天文的潮汐力影響,還會受到氣象(風和氣壓)的強烈影響,例如風暴潮。潮汐造成海洋和港灣口積水深度的改變,並且形成震盪的潮汐流,因此製作沿海地區潮汐流的預測在航海上是很重要的。在漲潮時會埋在海水中,而在退潮時會裸露出來的潮間帶,是潮汐造成的重要海洋生態。
……
物理學
潮汐物理學的歷史
牛頓在他的自然哲學的數學原理(1687)一書中以科學的研究奠定了用數學解釋潮汐發生的基礎力量[16][17]。牛頓首先應用牛頓萬有引力定律計算由太陽和月球吸引造成的潮汐[18],並且提供了引潮力最初的理論。但是牛頓的理論和他的後繼者是採用之前拉普拉斯的均衡理論,在很大的程度上是以近似值描述潮汐即使在覆蓋整個地球的非慣性海洋中也會發生[16]引潮力(或是相當於位能)對潮汐理論依然是有意義的,但做為一個中間的數值,而不是最終的結果;理論已經考慮地球動力學與潮汐的關係,而受到地形、地Ë球自轉和其它因素的影響[19]。
在1740年,在巴黎的法國皇家科學院提供獎金給最佳的潮汐理論 ,由丹尼爾·伯努利、Antoine Cavalleri、歐拉、和柯林·馬克勞林共享這筆獎金。
馬克勞林使用牛頓的理論顯示一個覆蓋了足夠深度海洋的單一平滑球體,在潮汐力的作用下會變形成為扁長的橢球體,而長軸就指向引起變形的天體。馬克勞林也是第一個寫下地球的柯里奧利力對運動的影響。
歐拉意識到在水平方向的力(引潮力)才是驅動潮汐的力(比垂直方向的起潮力大)。
在1744年,達朗貝爾研究潮汐的大氣方程式,但沒有包括轉動的因素。
皮埃爾-西蒙·拉普拉斯以偏微分方程的形式制訂有關海洋在水平的流動和海表面高度的系統,是第一件主要的潮汐動力理論,而且拉普拉斯潮汐方程在今天仍在使用。William Thomson, 1st Baron Kelvin重寫了拉普拉斯方程中的渦度項目,使方程式可以描述與解決驅動沿岸陷落波,也就是所知的克耳文波[20] [21] [22]。
其他人,包括克耳文與亨利·龐加萊繼續開發拉普拉斯理論,根據這些發展與E W布朗和Arthur Thomas Doodson的月球理論在1921年開發和發布[23],第一個現代化的引潮諧波形式:道森列出了388項潮汐頻率[24],其中有些方法現在仍被使用著[25]。
力
若以月球潮汐為例,作用於每單位質量的引潮力是月球的引力場在該單位質量的位置和在地心的矢量差。此每單位質量引潮力可分解為垂直 (即徑向) 分量 ![]() 和水平 (即切向) 分量
和水平 (即切向) 分量 ![]() 。簡化後,它們分別是
。簡化後,它們分別是
![]() 和
和 ![]() 。
。
其中 ![]() 是萬有引力常數,
是萬有引力常數,![]() 是月球質量,
是月球質量,![]() 是地球半徑,
是地球半徑,![]() 是地心與月心的距離,
是地心與月心的距離, ![]() 是該單位質量與地心的連線與地—月連線的夾角。
是該單位質量與地心的連線與地—月連線的夾角。
最高潮發生在正面向月球 ( ![]() ) 和正背向月球 (
) 和正背向月球 ( ![]() ) 兩位置。在該兩處
) 兩位置。在該兩處 ![]() 及
及 ![]() 。最低潮則發生在
。最低潮則發生在 ![]() 和
和 ![]() 兩位置。在該兩處
兩位置。在該兩處 ![]() 及
及 ![]() 。
。
數值上,![]() 是地球引力加速度
是地球引力加速度 ![]() 的千萬份之一 (
的千萬份之一 ( ![]() )。這個比例約莫等於一根火柴與一輛 2 公噸汽車重量之比。無論潮汐幅度如何,此垂直引潮力與海水的重量仍保持這比例 (因為它們均正比於質量)。 如此微弱的引潮力是不可能在
)。這個比例約莫等於一根火柴與一輛 2 公噸汽車重量之比。無論潮汐幅度如何,此垂直引潮力與海水的重量仍保持這比例 (因為它們均正比於質量)。 如此微弱的引潮力是不可能在 ![]() 的影響下能垂直把海水拉起或壓下。
的影響下能垂直把海水拉起或壓下。
事實上,海洋潮汐的發生是引潮力的水平分量 ( ![]() ) 起的作用,而不是垂直分量 (
) 起的作用,而不是垂直分量 ( ![]() )。 譬如,在
)。 譬如,在 ![]() 低潮) 至
低潮) 至 ![]() (高潮) 的範圍內,
(高潮) 的範圍內, ![]() 都是沿地球表面以單一相同方向作用這長達地球周界四份之一的海水。 如果以平衡潮理論來說,這樣把海水水平擠壓就會令海水的壓強在這大範圍內隨
都是沿地球表面以單一相同方向作用這長達地球周界四份之一的海水。 如果以平衡潮理論來說,這樣把海水水平擠壓就會令海水的壓強在這大範圍內隨 ![]() 緩慢增加。同時,海水保持著平衡,海面下增大了的壓強就會把海水水位推至適當高度,在正面向和正背向月球兩位置,海水的壓強最大,水位亦升得最高 (潮漲)。
緩慢增加。同時,海水保持著平衡,海面下增大了的壓強就會把海水水位推至適當高度,在正面向和正背向月球兩位置,海水的壓強最大,水位亦升得最高 (潮漲)。 ![]() 與
與 ![]() 雖屬同數量級 (一樣微弱) ,但只是前者能產生可觀察的效果, 因為它不須與地心吸力抗衡及可以有長達
雖屬同數量級 (一樣微弱) ,但只是前者能產生可觀察的效果, 因為它不須與地心吸力抗衡及可以有長達 ![]() 的作用距離[26]。
的作用距離[26]。
如果以動力潮理論來說,![]() 較
較 ![]() 重要, 它會把海水推動,形成潮流、潮波,把海水帶向潮漲位置[27]。
重要, 它會把海水推動,形成潮流、潮波,把海水帶向潮漲位置[27]。
的物理史,愛因斯坦的評語,使人感覺深切無奈!
嘆息『理性』與『感性』常有不共向遺憾也?
期許詞條之『理解』︰
Linear approximation
In mathematics, a linear approximation is an approximation of a general function using a linear function (more precisely, an affine function). They are widely used in the method of finite differences to produce first order methods for solving or approximating solutions to equations.

Tangent line at (a, f(a))
Definition
Given a twice continuously differentiable function ![]() of one real variable, Taylor’s theorem for the case
of one real variable, Taylor’s theorem for the case ![]() states that
states that
![]()
- where
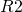 is the remainder term. The linear approximation is obtained by dropping the remainder:
is the remainder term. The linear approximation is obtained by dropping the remainder: 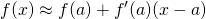 .
.
This is a good approximation for ![]() when it is close enough to
when it is close enough to ![]() ; since a curve, when closely observed, will begin to resemble a straight line. Therefore, the expression on the right-hand side is just the equation for the tangent line to the graph of
; since a curve, when closely observed, will begin to resemble a straight line. Therefore, the expression on the right-hand side is just the equation for the tangent line to the graph of ![]() at
at ![]() . For this reason, this process is also called the tangent line approximation.
. For this reason, this process is also called the tangent line approximation.
If ![]() is concave down in the interval between
is concave down in the interval between ![]() and
and ![]() , the approximation will be an overestimate (since the derivative is decreasing in that interval). If
, the approximation will be an overestimate (since the derivative is decreasing in that interval). If ![]() is concave up, the approximation will be an underestimate.[1]
is concave up, the approximation will be an underestimate.[1]
Linear approximations for vector functions of a vector variable are obtained in the same way, with the derivative at a point replaced by the Jacobian matrix. For example, given a differentiable function ![]() with real values, one can approximate
with real values, one can approximate ![]() close to
close to ![]() by the formula
by the formula
![]()
- The right-hand side is the equation of the plane tangent to the graph of
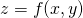 at
at 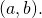
In the more general case of Banach spaces, one has
![]()
- where
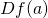 is the Fréchet derivative of
is the Fréchet derivative of  at
at  .
.
……
Applications
Optics
Gaussian optics is a technique in geometrical optics that describes the behaviour of light rays in optical systems by using the paraxial approximation, in which only rays which make small angles with the optical axis of the system are considered.[2] In this approximation, trigonometric functions can be expressed as linear functions of the angles. Gaussian optics applies to systems in which all the optical surfaces are either flat or are portions of a sphere. In this case, simple explicit formulae can be given for parameters of an imaging system such as focal distance, magnification and brightness, in terms of the geometrical shapes and material properties of the constituent elements.
Period of oscillation
The period of swing of a simple gravity pendulum depends on its length, the local strength of gravity, and to a small extent on the maximum angle that the pendulum swings away from vertical, θ0, called the amplitude.[3] It is independent of the mass of the bob. The true period T of a simple pendulum, the time taken for a complete cycle of an ideal simple gravity pendulum, can be written in several different forms (see Pendulum (mathematics) ), one example being the infinite series:[4][5]
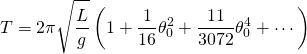
- where L is the length of the pendulum and g is the local acceleration of gravity.
However, if one takes the linear approximation (i.e. if the amplitude is limited to small swings,[Note 1] ) the period is:[6]

- In the linear approximation, the period of swing is approximately the same for different size swings: that is, the period is independent of amplitude. This property, called isochronism, is the reason pendulums are so useful for timekeeping.[7] Successive swings of the pendulum, even if changing in amplitude, take the same amount of time.
Electrical resistivity
The electrical resistivity of most materials changes with temperature. If the temperature T does not vary too much, a linear approximation is typically used:
![]()
- where
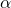 is called the temperature coefficient of resistivity,
is called the temperature coefficient of resistivity,  is a fixed reference temperature (usually room temperature), and
is a fixed reference temperature (usually room temperature), and 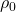 is the resistivity at temperature
is the resistivity at temperature 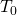 . The parameter
. The parameter 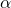 is an empirical parameter fitted from measurement data. Because the linear approximation is only an approximation,
is an empirical parameter fitted from measurement data. Because the linear approximation is only an approximation, 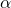 is different for different reference temperatures. For this reason it is usual to specify the temperature that
is different for different reference temperatures. For this reason it is usual to specify the temperature that 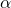 was measured at with a suffix, such as
was measured at with a suffix, such as 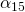 , and the relationship only holds in a range of temperatures around the reference.[8] When the temperature varies over a large temperature range, the linear approximation is inadequate and a more detailed analysis and understanding should be used.
, and the relationship only holds in a range of temperatures around the reference.[8] When the temperature varies over a large temperature range, the linear approximation is inadequate and a more detailed analysis and understanding should be used.
能與文本『同其義』︰
Linearization in Physics/Mechanics
mechanics includes methods for linearizing the generated equations of motion (EOM) about an operating point (also known as the trim condition). Note that this operating point doesn’t have to be an equilibrium position, it just needs to satisfy the equations of motion.
Linearization is accomplished by taking the first order Taylor expansion of the EOM about the operating point. When there are no dependent coordinates or speeds this is simply the jacobian of the right hand side about ![]() and
and ![]() . However, in the presence of constraints more care needs to be taken. The linearization methods provided here handle these constraints correctly.
. However, in the presence of constraints more care needs to be taken. The linearization methods provided here handle these constraints correctly.
Background
In mechanics we assume all systems can be represented in the following general form:
![]()
![]()
![]()
![]()
![]()
In this form,
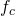 represents the configuration constraint equations
represents the configuration constraint equations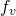 represents the velocity constraint equations
represents the velocity constraint equations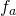 represents the acceleration constraint equations
represents the acceleration constraint equations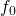 and
and 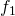 form the kinematic differential equations
form the kinematic differential equations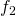 ,
, 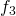 , and
, and 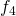 form the dynamic differential equations
form the dynamic differential equations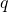 and
and 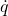 are the generalized coordinates and their derivatives
are the generalized coordinates and their derivatives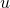 and
and 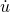 are the generalized speeds and their derivatives
are the generalized speeds and their derivatives is the system inputs
is the system inputs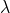 is the Lagrange multipliers
is the Lagrange multipliers
This generalized form is held inside the Linearizer class, which performs the actual linearization. Both KanesMethod and LagrangesMethod objects have methods for forming the linearizer using theto_linearizer class method.
A Note on Dependent Coordinates and Speeds
If the system being linearized contains constraint equations, this results in not all generalized coordinates being independent (i.e. ![]() may depend on
may depend on ![]() ). With
). With ![]() configuration constraints, and
configuration constraints, and ![]() velocity constraints, there are
velocity constraints, there are ![]() dependent coordinates and
dependent coordinates and ![]() dependent speeds.
dependent speeds.
In general, you may pick any of the coordinates and speeds to be dependent, but in practice some choices may result in undesirable singularites. Methods for deciding which coordinates/speeds to make dependent is behind the scope of this guide. For more information, please see [Blajer1994].
Once the system is coerced into the generalized form, the linearized EOM can be solved for. The methods provided in mechanics allow for two different forms of the linearized EOM:
![]() ,
, ![]() ,
, ![]()
In this form, the forcing matrix is linearized into two separate matrices ![]() and
and ![]() . This is the default form of the linearized EOM. The resulting equations are:
. This is the default form of the linearized EOM. The resulting equations are:
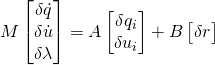
where
![]()
![]()
![]()
Note that ![]() and
and ![]() are just the independent coordinates and speeds, while
are just the independent coordinates and speeds, while ![]() and
and ![]() contains both the independent and dependent coordinates and speeds.
contains both the independent and dependent coordinates and speeds.
![]() and
and ![]()
In this form, the linearized EOM are brought into explicit first order form, in terms of just the independent coordinates and speeds. This form is often used in stability analysis or control theory. The resulting equations are:
![]()
where
![]()
![]()
To use this form set A_and_B=True in the linearize class method.
……
Linearizing Lagrange’s Equations
Linearization of Lagrange’s equations proceeds much the same as that of Kane’s equations. As before, the process will be demonstrated with a simple pendulum system:
………
或可通達矣◎