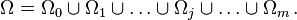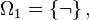假使我們回顧《 λ 運算︰概念導引《一》》一文︰

《説文解字》：

名，自命也。从口，从夕。夕者，冥也。冥不相見，故以口自名。

古來『名字』的傳統，幼時口呼『命名』，成年書寫『取字』。

許多讀過『λ 運算』的人，多半覺得它既『難懂』又『難解』。這是有原因的，如果用『抽象辦法』談論著『抽象事物』，又不知道為何如此表述當然『難懂』；假使不能『困思勉行』多次的『深思熟慮』，以至於能夠一旦了悟那就自然『難解』。通常越是『基本 』的概念，由於太過『直覺』了，反而容易『誤解』。就像化學元素『週期表』上的元素不過一一八個，它所構成的世界卻是千嬌萬媚繁多複雜，要講『鐵』的『性質』與『作用』，也許一大本書都不能窮盡，但換個方向說鐵不就是日用之物的嗎？

邱奇發展『λ 運算』Lambda calculus，這裡的『calculus』不是指『微積分』，是用著『函式』Function 和『變元』Variable 的概念，來談論『計算』一事是什麼？複雜的『函式』是如何清晰明白無歧異的『結構』而成？『變元』的『替換』Substitution 規則，要如何系統化的處理變元替換時『異物同名』衝突之問題？如果從『函式求值』上講，一個『λ 表達式』用著怎樣的『規則』可以『轉換』成為『同等』equivalent 的另一個 λ 表達式呢？……種種。假使給定了兩個『λ 表達式』是否會有一個普適的『演算法』能夠判定彼此間的『同等性』呢？……等等。

『λ 表達式』可以用『數學歸納法』定義如下︰

變元集合
抽象符號 『 λ  』與『 . 』，符號本身不是λ 表達項
結構括號 『 ( 』與『 ) 』，括號本身不是λ 表達項

λ 表達式的集合 ，由下面三條規則歸納界定︰

一、如果 ，那麼

二、如果 而且 ，那麼

三、如果 ，那麼

假如使用數學上函數的觀點來解釋，『第一條』規則是說︰『變數』是一個『λ 表達式』。『第二條』規則用以抽象建構單一變數的『函數』，變數 是『函數』的『輸入之數』， 是『函數』的『計算表達式』，結構括號表示『函數』的在表達式裡的範圍。『第三條』規則是應用『函數求值規則』，假使該應用合理的話，計算表達式 在 表達式下的值。舉個例子說︰

假設 是變數，所以 是 λ 表達式，因此
是一個函數的 λ 表達式，因是
是一個應用求值的 λ 表達式。

……

，也許讀者已發現『 λ表達式』的定義方法，和命題邏輯 ── 引自 WiKi ──  是那麼的相似︰

命題演算是一個形式系統 ，它的公式按如下方式構造：

• 是由名為「命題符號」或「命題變量」之元素所組成的有限集合。語法上來說，它們是形式語言 最基本的元素，亦被稱之為「原子公式」或「終端元素」。在接著的例子中， 內的元素一般寫作字母 p, q, r 之類的形式。

• 是名為「運算元符號」或「邏輯運算符」之元素所組成的有限集合。集合 被劃分成如下等不相交的子集：

在此一劃分中， 是指元數為 的運算元符號所構成的集合。

在更熟知的命題演算中， 一般被劃分如下：

一種常用的做法是把常數邏輯值當作一種零元運算元，即：

有些作者用 ~ 來替代 ¬ ，也有的用 & 或 來取替 。邏輯值所構成的集合也有許多不同的符號表示，如 {假,真} 、 {F,T} 、 {0,1} 和 {, } ，這些都常見於各個論著之中。

• 依據所使用的精確形式文法或文法形式化，可能需要以左括號 “(” 和右括號 “)”作語法上的輔助，用來完成公式的構造。

的語言，亦稱之為「公式」或「合式公式」的集合，可由如下規則被歸納或遞迴地定義：

1. 基本元素： 內的任何元素都是 的公式。
2. 步驟 (a)：如果 p 是公式，則 ¬p 也會是公式。
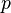
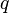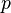
3. 步驟 (b)：如果 p 和 q 是公式，則 ( ) 、 ( ) 、 (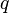) 和 () 也都會是公式。
4. 封閉性：其他都不會是 的公式。

透過重複應用這三個規則，可以建構出複雜的公式來。例如：

1. 依規則 1，p 是公式。
2. 依規則 2，¬p 是公式。
3. 依規則 1，q 是公式。
4. 依規則 3，(¬p ∨ q) 是公式。

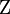• 是「轉換規則」（當作為邏輯應用時則稱之為「推理規則」）之所構成的有限集合。

• 是「起始點」（當得到邏輯解釋時則稱之為「公理」）所構成的有限集合。

這是否給了人們啟發，通熟了一種『抽象系統』論述，常常有助於理解另一種『抽象系統』論述。這不僅是因為說法的『相似性』，更因為對於『概念』引入、『術語』展開、『架構』呈現、…已經有過『經驗』，許多事物不會超出『預期』之外，因此較能掌握『重點』，知道核心『關鍵』是什麼之故。

『命題邏輯』 Propositional calculus 是一種『真、假』二值邏輯。在這個邏輯體系裡，所有命題『非真即假』。它的主要特徵可由『矛盾蘊函萬有』，叫做『爆炸原理』，來概括︰

一、 假設 甲 與 非甲 皆真 【矛盾】

二、 甲真 【來自於一之中『與』 and 的詞義】

三、甲 或 萬有 為真 【來自於二以及『或』 or 的詞義】

四、非甲 【來自於一之中『與』 and 的詞義】

五、 萬有 【來自於三和四，理則歸結】

所以證明了『矛盾 → 萬有』為真。

或許可以說近代『邏輯』相關的零零種種研究，多半與一個稱之為『羅素悖論』︰

有一位理髮師宣稱，他為所有不為自己理髮的人理髮，請問他為不為自己理髮？ ── 引自《{x|x ∉ x} ！！？？》──

者有千絲萬縷的聯繫！同一篇文章中所講到的︰邏輯學家為了說明邏輯推導是否合理、有效和合法，構造了『真值表』︰

P ，非 P P ，   ~P	Q	P 且 Q P ‧ Q	P 或 Q P + Q	若 P 則 Q P → Q	非 P 或 Q ~P + Q
真 ，假  T      F	真 T	真 T	真 T	真 T	真 T
真 ，假  T      F	假 F	假 F	真 T	假 F	假 F
假 ，真  F      T	真 T	假 F	真 T	真 T	真 T
假 ，假   F       F	假 F	假 F	假 F	真 T	真 T

。真值表考慮了陳述句所有的真假可能狀況，如果兩個陳述句 ── 比方說 P → Q 和 ~P + Q ──，在每一種狀況裡都真假相同，那麼他們在邏輯上表示同樣的陳述，只不過穿著不同說法的外衣 。假使有一個陳述句在所有的真假可能狀況裡頭都是真的，這稱之為『恆真句』，舉例說 P + ~P。恆真句構成了論述合理有效推論的基礎。就讓我們說說有名的『三段論』吧︰

若 P 則 Q
因 P
故 Q

，把這個推理改寫成 ((P→Q)‧P)→Q ，那它將是個恆真句。雖然『 P 或非 P 』是個恆真句，但是彷彿像句空話，什麼也沒有說，事實上它說︰凡是陳述非真即假，假使 P 是真的，那麼非 P 一定是假的。這就是大名鼎鼎的『矛盾律』！可是那要怎麼看『明天可能會下雨』或『明天可能不會下雨』呢？好似『想非想非非想』一般 ，邏輯學的路途依然遙遠！！

，這個『真值表』詮釋，也就是『數理邏輯』中『埃爾布朗解釋』Herbrand interpretation  ，紀念英年早逝的『雅克‧埃爾布朗』 Jacques Herbrand 對『機器證明』基礎之貢獻︰

In mathematical logic, a Herbrand interpretation is an interpretation in which all constants and function symbols are assigned very simple meanings. Specifically, every constant is interpreted as itself, and every function symbol is interpreted as the function that applies it. The interpretation also defines predicate symbols as denoting a subset of the relevant Herbrand base, effectively specifying which ground atoms are true in the interpretation. This allows the symbols in a set of clauses to be interpreted in a purely syntactic way, separated from any real instantiation.

The importance of Herbrand interpretations is that, if any interpretation satisfies a given set of clauses S then there is a Herbrand interpretation that satisfies them. Moreover, Herbrand’s theorem states that if S is unsatisfiable then there is a finite unsatisfiable set of ground instances from the Herbrand universe defined by S. Since this set is finite, its unsatisfiability can be verified in finite time. However there may be an infinite number of such sets to check.

It is named after Jacques Herbrand.

如此所謂『原子』 atom ，或說『邏輯原子』，意指『真假陳述』的『最小單元』，其內沒有其它的『邏輯結構』之『基本命題』。如是所謂『子句』 clause 就是有特定『邏輯結構』的『命題』︰

。由於『邏輯運算符號』彼此間的『邏輯等價』性，使得我們可以選擇『機器證明』的合適『句式』，在盡可能不失去『一般性』的狀況下建構該程式語言。也可以說『特定性』是『實務』考量下的結果。因此我們可以明白『霍恩子句』 Horn clause  ︰

A Horn clause is a clause (a disjunction of literals) with at most one positive, i.e. unnegated, literal.

Conversely, a disjunction of literals with at most one negated literal is called a dual-Horn clause.

A Horn clause with exactly one positive literal is a definite clause; a definite clause with no negative literals is sometimes called a fact; and a Horn clause without a positive literal is sometimes called a goal clause (note that the empty clause consisting of no literals is a goal clause). These three kinds of Horn clauses are illustrated in the following propositional example:

	Disjunction form	Implication form	Read intuitively as
Definite clause	¬p ∨ ¬q ∨ … ∨ ¬t ∨ u	u ← p ∧ q ∧ … ∧ t	assume that, if p and q and … and t all hold, then also u holds
Fact	u	u	assume that u holds
Goal clause	¬p ∨ ¬q ∨ … ∨ ¬t	false ← p ∧ q ∧ … ∧ t	show that p and q and … and t all hold [note 1]

In the non-propositional case, all variables in a clause are implicitly universally quantified with scope the entire clause. Thus, for example:

¬ human(X) ∨ mortal(X)

stands for:

∀X( ¬ human(X) ∨ mortal(X) )

which is logically equivalent to:

∀X ( human(X) → mortal(X) )

Horn clauses play a basic role in constructive logic and computational logic. They are important in automated theorem proving by first-order resolution, because the resolvent of two Horn clauses is itself a Horn clause, and the resolvent of a goal clause and a definite clause is a goal clause. These properties of Horn clauses can lead to greater efficiencies in proving a theorem (represented as the negation of a goal clause).

Propositional Horn clauses are also of interest in computational complexity, where the problem of finding truth value assignments to make a conjunction of propositional Horn clauses true is a P-complete problem (in fact solvable in linear time), sometimes called HORNSAT. (The unrestricted Boolean satisfiability problem is an NP-complete problem however.) Satisfiability of first-order Horn clauses is undecidable.

的由來，它的『重要性』以及可能的『限制性』。進而理解『證明理論』 Proof Theory 所講的『 resolution 』邏輯推導歸結與『unification』 變元替換一致化。且清楚明白『歸謬證法』 proof by refutation 在『證明理論』中的主導地位。