《 
》網的本義就是『結網捕魚』，如今我們已經討論過多種『網』，它們雖然名稱不同，許多性質卻是一樣的。為了避免有『漏網之魚』，在此特補之以
《物理哲學·中中》之文摘︰
『理所當然』未必一定是『理有必然』，就像說『改善交通』應該『多開條路』的吧！！德國數學家迪特里希‧布雷斯 Dietrich Braess 宣稱︰
在一個交通網上新闢一條通路，反而可能使得用路所需的時間增加了；這一條新闢的道路，非但無助於減少交通遲滯，卻很可能會降低了整個交通網的服務水準。
納什均衡， 
如果 
，最佳選擇
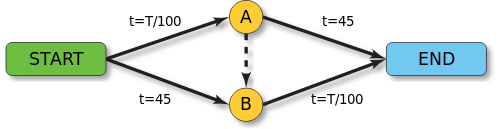
那麼布雷斯的說法有道理嗎？假使請讀者設想從『起點』 Start 到『終點』 End ，原有『兩個選擇』，要不經由『A 點』，否則就得經過『B 地』。人們從『經驗』上『知道』走 
路段要花的時間依賴『車流量』，大概需要 
分鐘，如果選擇先『到 B』，一般與『車流量』無關，是『固定的』四十五分鐘，可是 
要花的時間也依賴於『車流量』，時間差不多與『A』相同，也是 
分鐘。因此『理性』考慮『最短時間』，將會是『比較兩者』的『時間差』作選擇的吧？最後達到了『博奕論』Game Theory 所說的『納什均衡』 Nash equilibrium ，此時無論怎麽選擇『所需總時間』是一樣的 ，也就是說，如果假設一天平均有四千輛車經過『Start-End』，大概將『各取一半』，其中有兩千輛走『A 點』，另兩千輛經『B 處』的吧！『今有人』為著『改善交通』，於是乎在『A、B 兩地』間，開了一條『高速道路』 ，『以為能』縮短『所需總時間』，結果卻是吃力不討好『適得其反』，這又為什麼的呢？？因為一天最多不過有四千輛車，這樣 
不是比 
要小的嗎？由於 ，當然接著走 
的吧，到了『B 地』之後，依然還是 
能不是比 
小的嗎？於是乎，所有『非傻鳥』者『必走』 之『陽關道』，因此就 的了！！
現今這稱之為『布雷斯悖論』。那麼『一時』與『長久』，以及『部份』和『整體』 ，又該怎麽說的呢？？
及
《物理哲學·中下》的文引︰
經驗形成法則？？
假使有人想作『傻鳥』嘗試走『過去習慣』的道路，可能是 
，或許是 
，結果 
，果真是『傻鳥』的耶！！
現象已然形成，現實已經造就，事理能夠不自圓其說的嗎？？如此多年之後，這就變成了經驗法則，大概沒人會相信曾經有過更好的選擇的吧！！
那麼一個人要是『開通思路』，他是否『推理』會變得更慢的呢？也許『豆鵝狐人』的回答是︰人類的『思維』一般會形成『定勢』 ，因此通常只見着『陽關道』，少會過『獨木橋』，故而很難發生布雷斯的悖論，還是『思多識廣』的好吧！但是告誡勇闖新世界的人們，小心所創作的『人工智慧』機器，最好不要一不小心，它卻變成『傻鳥』的了？？
這樣說來喬治‧波利亞的『怎樣解題』之法
喬治‧波利亞
George Pólya
suggests the following steps when solving a mathematical problem:
1. First, you have to understand the problem.
2. After understanding, then make a plan.
3. Carry out the plan.
4. Look back on your work. How could it be better?
If this technique fails, Pólya advises: “If you can’t solve a problem, then there is an easier problem you can solve: find it.” Or: “If you cannot solve the proposed problem, try to solve first some related problem. Could you imagine a more accessible related problem?”
喬治‧波利亞長期從事數學教學，對數學思維的一般規律有深入的研究，一生推動數學教育。一九五四年，波利亞寫了兩卷不同於一般的數學書《Induction And_Analogy In Mathematics》與《Patterns Of Plausible Inference》探討『啟發式』之『思維樣態』，這常常是一種《數學發現》之切入點，也是探尋『常識徵候』中的『合理性』根源。舉個例子來說，典型的亞里斯多德式的『三段論』 syllogisms ︰
真， 
真。
如果對比著『似合理的』Plausible 『推理』︰
真， 更可能是真。
這種『推理』一般稱之為『肯定後件』 的『邏輯誤謬』。因為在『邏輯』上，這種『形式』的推導，並不『必然的』保障『歸結』一定是『真』的。然而這種『推理形式』是完全沒有『道理』的嗎？如果從『三段論』之『邏輯』上來講，要是 為『假』， 也就『必然的』為『假』。所以假使 為『真』之『必要條件』 為『真』，那麼 不該是『更可能』是『真』的嗎？？
，一點不因提出時間古早，依然是管用的！若說應用之妙在於『能想人所不能想』和『能用人所不能用』，此法終究使人困惑？然而一個『困思勉行』者時有感悟，一位『真積力』者，己不能通，神自來通，又何困惑之有的呢！！