何謂『大哉問』?比方說︰僅藉維基百科『詞條』可以學
動力學
動力學(Dynamics)是古典力學的一門分支,主要研究運動的變化與造成這變化的各種因素。換句話說,動力學研究力對物體之運動所造成的影響。運動學則是純粹描述物體的運動,完全不考慮導致運動的因素。 更仔細地說,動力學研究由於力的作用,物理系統怎樣改變。動力學的基礎定律是艾薩克·牛頓提出的牛頓運動定律。對於任意物理系統,只要知道其作用力的性質,引用牛頓運動定律,就可以研究這作用力對於這物理系統的影響。 在古典電磁學裏,物理系統的動力狀況涉及了古典力學與電磁學,需要使用牛頓運動定律、馬克士威方程式、勞侖茲力方程式來描述 。動力學是機械工程與航空工程的基礎課程。
乎??難答也!關鍵之處在『曾經入門』與否耶!!
『詞條』或能喚醒『名目記憶』,恐無法深入『概念內涵』吧◎
就像說
力
力是一種造成物體加速的影響,也可以感官體驗為一種推擠或拖拉,這會造成物體改變方向、改變速度、暫時性或永久性的形變 。力會迫使改變物體的運動狀態。[1]力是一個向量,具有大小和方向。
之『定義』常生疑惑啊!?
牛頓運動定律
牛頓運動定律(Newton’s laws of motion)描述物體與力之間的關係,被譽為是古典力學的基礎。這定律是英國物理泰斗艾薩克·牛頓所提出的三條運動定律的總稱,其現代版本通常這樣表述 :[1]:88f[2]
- 第一定律:存在某些參考系,在其中,不受外力的物體都保持靜止或等速直線運動。
- 第二定律:施加於物體的淨外力等於此物體的質量與加速度的乘積。
- 第三定律:當兩個物體互相作用時,彼此施加於對方的力,其大小相等、方向相反。
牛頓在發表於1687年7月5日的鉅著《自然哲學的數學原理》裏首先整理出這三條定律。[3]應用這些定律,牛頓可以分析各種各樣的動力運動。例如,在此書籍第三卷,牛頓應用這些定律與牛頓萬有引力定律來解釋克卜勒行星運動定律。

在鉅著《自然哲學的數學原理》1687年版本裡,以拉丁文撰寫的牛頓第一定律及牛頓第二定律。
概述
在應用牛頓定律之前,必需先將物體理想化為質點[註 1]。所謂「質點」是指物理學中理想化的模型,在考慮物體的運動時,將物體的形狀、大小、質地、軟硬等性質全部忽略,只用一個幾何點和一個質量來代表此物體。質點模型適用的範圍是當與分析所涉及的距離相比較,物體的尺寸顯得很微小,或我們只考慮物體受的外力,物體本身的內部結構 、形變、旋轉、溫度等對於分析並不重要。舉例而言,在分析行星環繞恆星的軌道運動時,行星與恆星都可以被理想化為質點。
原初版本的牛頓運動定律只適用於描述質點的動力學,不具有足夠功能來描述剛體與可變形體的運動。1750年,歐拉在牛頓定律的基礎上,推導出能夠應用於剛體的歐拉運動定律。後來,這定律又被應用於假定為連續介質的可變形體。[4]假若用一群離散質點的組合來代表物體,其中每一個質點都遵守牛頓定律,則可以從牛頓定律推導出歐拉運動定律。不論如何,歐拉運動定律可以直接視為專門描述宏觀物體運動的公理,與物體內部結構無關。[5]在這裏,宏觀物體指的是尺度遠遠大於粒子尺度的物體。
牛頓運動定律只成立於慣性參考系,又稱為牛頓參考系。有些學者喜歡將第一定律作為根本,而將慣性參考系視作第一定律的延伸,也就是說在他們看來,第一定律可以用來定義慣性參考系。假若採用這觀點,則由於只有從慣性參考系觀察,第二定律才成立,所以,不能從第二定律以特例的方式來推導出第一定律。另外又有一些學者將第一定律視為第二定律的推論。特別注意,慣性參考系的概念是在牛頓之後很久才發展成功。[6][7]
故爾
歐拉運動定律
歐拉運動定律(Euler’s laws of motion)是牛頓運動定律的延伸,可以應用於多粒子系統運動或剛體運動,描述多粒子系統運動或剛體的平移運動、旋轉運動分別與其感受的力、力矩之間的關係 。在艾薩克·牛頓發表牛頓運動定律之後超過半個世紀,於1750年 ,萊昂哈德·歐拉才成功地表述了這定律。[1][2]
剛體也是一種多粒子系統,但理想剛體是一種有限尺寸,可以忽略形變的固體。不論是否感受到作用力,在剛體內部,點與點之間的距離都不會改變。
歐拉運動定律也可以加以延伸,應用於可變形體(deformable body)內任意部分的平移運動與旋轉運動。
剛體
歐拉第一運動定律
歐拉第一定律表明,從某慣性參考系觀測,施加於剛體的淨外力 ,等於剛體質量與質心加速度的乘積。[3]歐拉第一定律以方程式表達為
![]()
- 其中,
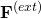 是剛體感受到的淨外力,
是剛體感受到的淨外力,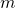 、
、 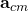 分別是剛體的質量、質心加速度。
分別是剛體的質量、質心加速度。
剛體的平移運動等同於位於其質心、具有其質量的粒子,感受到同樣的淨外力,而呈現的運動。
導引
思考由 ![]() 個粒子組成的多粒子系統,其質心位置
個粒子組成的多粒子系統,其質心位置 ![]() 為
為
![]() ;
;
其中,![]() 、
、 ![]() 分別為第
分別為第 ![]() 個粒子的質量、位置,
個粒子的質量、位置,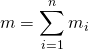 是系統的質量。
是系統的質量。
質心速度 ![]() 為
為
![]() ;
;
其中,![]() 是第
是第 ![]() 個粒子的速度。
個粒子的速度。
質心加速度 ![]() 為
為
![]() ;
;
其中,![]() 是第
是第 ![]() 個粒子的加速度。
個粒子的加速度。
第 ![]() 個粒子感受到的力
個粒子感受到的力 ![]() 為
為
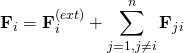 ;
;
其中,![]() 是這粒子感受到的外力,
是這粒子感受到的外力,![]() 是第
是第 ![]() 個粒子施加於第
個粒子施加於第 ![]() 個粒子的內力。
個粒子的內力。
系統感受到的淨力 ![]() 是所有粒子感受到的力的向量和:
是所有粒子感受到的力的向量和:
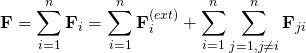 。
。
根據牛頓第三定律,內力與其反作用力的關係為
![]() 。
。
所以,所有粒子彼此施加於對方的內力的向量和為零,淨力等於所有外力的向量和 (淨外力 ![]() ):
):
 。
。
根據牛頓第二定律,第 ![]() 個粒子感受到的力
個粒子感受到的力 ![]() 與這粒子的加速度之間的關係為
與這粒子的加速度之間的關係為
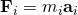 。
。
總和所有粒子所感受到的力,
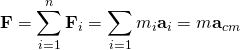 。
。
所以,淨外力 ![]() 與質心加速度的關係為
與質心加速度的關係為
![]() 。
。
動量守恆定律
多粒子系統的動量 ![]() 是組成這系統的所有粒子的動量的向量和:
是組成這系統的所有粒子的動量的向量和:
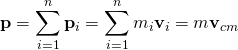 ;
;
其中,![]() 是第
是第 ![]() 個粒子的動量。
個粒子的動量。
歐拉第一定律又可以表達為
![]() 。
。
假設淨外力為零,則系統的動量守恆。
歐拉第二運動定律
歐拉第二定律表明,設定某慣性參考系的固定點O(例如,原點)為參考點,施加於剛體的淨外力矩,等於角動量的時間變化率。歐拉第二定律以方程式表達為
![]() ;
;
其中,![]() 是對於點O淨外力矩,
是對於點O淨外力矩,![]() 是對於點O的角動量。
是對於點O的角動量。
導引
思考由 ![]() 個粒子組成的多粒子系統。對於點O,第
個粒子組成的多粒子系統。對於點O,第 ![]() 個粒子的角動量
個粒子的角動量 ![]() 為
為
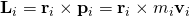 。
。
![]() 對於時間的導數為
對於時間的導數為
![]() 。
。
根據牛頓第二定律,施加於第 ![]() 個粒子的力
個粒子的力 ![]() 是這粒子的質量與加速度的乘積。所以,
是這粒子的質量與加速度的乘積。所以,![]() 對於時間的導數為
對於時間的導數為
![]() 。
。
第 ![]() 個粒子所感受到的淨力矩
個粒子所感受到的淨力矩 ![]() 為
為 ![]() 。所以,
。所以,![]() 的關係為
的關係為
![]() 。
。
總和所有粒子所感受到的淨力矩,系統所感受到的淨力矩 ![]() 與其角動量
與其角動量 ![]() 的關係為
的關係為
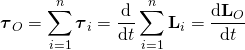 。
。
- 第
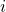 個粒子所感受到的淨力
個粒子所感受到的淨力 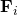 為
為 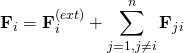 。
。
第 ![]() 個粒子所感受到的淨力矩
個粒子所感受到的淨力矩 ![]() 為
為
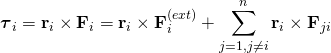 。
。
物體感受到的淨力矩 ![]() 為:
為:
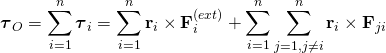 。
。
應用牛頓第三定律,
![]() ;
;
其中,![]() 是從粒子
是從粒子 ![]() 到粒子
到粒子 ![]() 的位移向量。
的位移向量。
假設這系統的粒子遵守強版牛頓第三定律,即粒子運動為古典運動,速度超小於光速,則 ![]() 與
與 ![]() 同向,叉積為零。那麼,物體感受到的淨力矩是所有外力矩的向量和
同向,叉積為零。那麼,物體感受到的淨力矩是所有外力矩的向量和 ![]() :
:
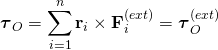 。
。
這樣,可以得到歐拉第二定律方程式
![]() 。
。
假設施加於系統的淨外力矩為零,則系統的角動量的時間變化率為零,系統的角動量守恆。
相對於質心的歐拉第二運動定律
所有粒子所感受到的淨力矩的向量和為
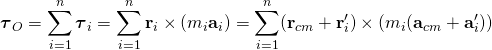 ;
;
其中,![]() 、
、 ![]() 分別是第
分別是第 ![]() 個粒子相對於質心的相對位移與相對加速度。
個粒子相對於質心的相對位移與相對加速度。
注意到所有粒子的相對位移與相對加速度,其向量和分別為零,所以,
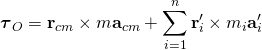 。
。
現在,假設將質心設定為參考點,則 ![]() ,方程式變為
,方程式變為
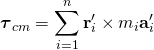 。
。
以質心為參考點,角動量 ![]() 為
為
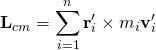 。
。
所以,不論質心參考系是否為慣性參考系(即不論質心是否呈加速度運動),以質心為參考點,淨外力矩等於角動量的時間變化率:
![]() 。
。
往往不知所云呦?!
何不就嘗試自己看天下哩☆
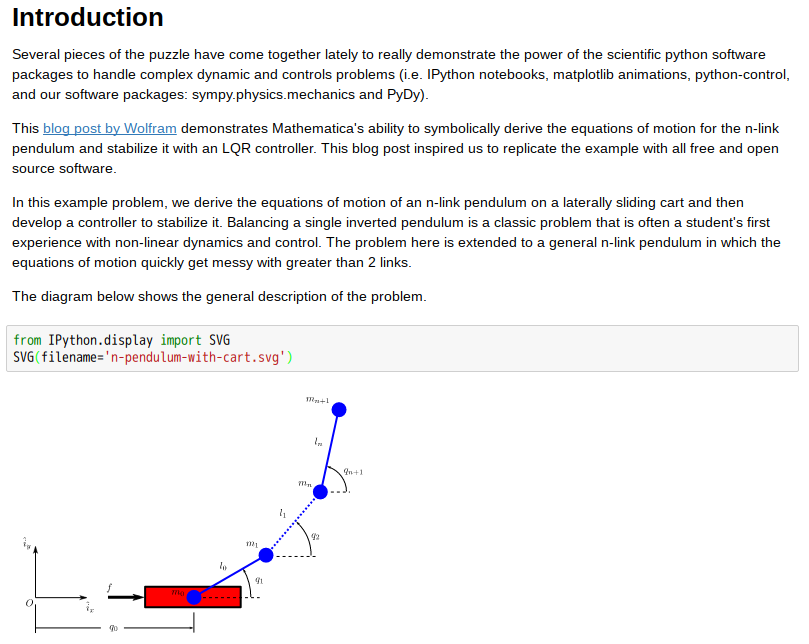
Dynamics with Python