1 | 5 月 | 2018 | FreeSandal

偉大的教育理念︰孔子的『因材施教』和『有教無類』。

學習文摘︰

子曰︰『吾十有五而志於學；三十而立；四十而不或；五十而知天命；六十而耳順；七十而從心所欲，不踰矩。』

子曰：『學而時習之，不亦說乎？有朋自遠方來，不亦樂乎？人不知而不慍，不亦君子乎？』

子曰：『學而不思則罔，思而不學則殆。』

子曰：『由，誨女知之乎。知之為知之，不知為不知，是知也。』

子曰：『不憤不啟，不悱不發，舉一隅不以三隅反，則不復也。』

─── 《樹莓一月記；》

今天是勞動節︰

1866年，第一國際日內瓦會議提出八小時工作制的口號。1886年5月1日，以美國芝加哥為中心，在美國舉行了約35萬人參加的大規模罷工和示威遊行^[1]，示威者要求改善勞動條件，實行八小時工作制。5月3日芝加哥政府出動警察鎮壓，並向人群開槍，打死了四個人，受傷者無數。這件事引起了整個芝加哥城沸騰，各工會決議於5月4日在乾草市廣場舉行群眾大會，約2,500名勞工，情緒雖然激昂，過程卻非常和平。一場突如其來的大雨將群眾淋得只剩兩百多人左右。正當勞工正要開始收場時，忽然開來一隊180名全副武裝的警察，將現場包圍起來，命令他們馬上解散。就在雙方在爭論的時候，突然發生了爆炸事件，場面頓時大亂。在黑暗中，警察向群眾開火，人們四處逃竄。共計有十名勞工當場被打死，而警察也因彼此誤射而死傷慘重，這就是歷史上聞名的「乾草市廣場慘案」。

事後警察與新聞界一口咬定是無政府主義者丟的炸彈，要求處以極刑。因此，警方大事逮捕勞工領袖，最後以謀殺罪起訴八個人。其中有五個人那晚根本沒到會場，只不過他們都是工會運動的活躍份子，警方正好藉機一網打盡。

審判最後，除了一人被判十五年外，二人被判無期徒刑外，五人都判死刑。而其中的一位工運領袖奧古斯都.史比司（August Spies）在臨刑前說：「總有一天，我們的沈默，會遠比今天你們所要壓制的言論更為宏亮有力！」^[2]。直到1889年，為了紀念這段壯烈的歷史，在巴黎舉行的第二國際成立大會通過決議，將5月1日定為國際勞工節，要求各國的勞工共同努力，為八小時工作日而奮鬥。今日有「乾草市場烈士紀念碑」（Haymarket Martyrs’ Monument）以紀念此事殉難者。

美國直到1935年羅斯福總統執政時，八小時工作制定於法律中才予以確立。

不知為何突然想起了那首

【佚名詩】

大地藏無盡，
勤勞資有生；
念哉斯意厚，
努力事春耕。

？一時覺得人積累數千年之科技與文明，竟還解決不了

公平合理

分配的問題？？曾有所謂『勞』『心』與『勞』『力』貢獻大小之論！納罕要是天生我才必有用，如何談『用』『高』及『用』『低』理則呢！！

忽見窗外又『日上三竿』，努力『學而時習之，不亦說乎？』︰

Motion in space of a rigid body, and the inertia matrix

The scalar moments of inertia appear as elements in a matrix when a system of particles is assembled into a rigid body that moves in three-dimensional space. This inertia matrix appears in the calculation of the angular momentum, kinetic energy and resultant torque of the rigid system of particles.^[3]^[4]^[5]^[6]^[25]

Let the system of particles $P i, i = 1, \dots, n$ be located at the coordinates $r i$ with velocities $v i$ relative to a fixed reference frame. For a (possibly moving) reference point $R$ , the relative positions are

$\displaystyle \Delta \mathbf {r} _{i}=\mathbf {r} _{i}-\mathbf {R}$

and the (absolute) velocities are

$\displaystyle \mathbf {v} _{i}={\boldsymbol {\omega }}\times \Delta \mathbf {r} _{i}+\mathbf {V} _{\mathbf {R} }$

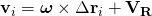
where

ω

is the angular velocity of the system, and

V R

is the velocity of

R

Angular momentum

Note that the cross product can be equivalently written as matrix multiplication by combining the first operand and the operator into a, skew-symmetric, matrix, $[b]$ , constructed from the components of $b = (b x, b y, b z)$ :

$\displaystyle {\begin{aligned}\mathbf {b} \times \mathbf {y} &\equiv \lbrack \mathbf {b} \rbrack \mathbf {y} \\\lbrack \mathbf {b} \rbrack &\equiv {\begin{bmatrix}0&-b_{z}&b_{y}\\b_{z}&0&-b_{x}\\-b_{y}&b_{x}&0\end{bmatrix}}.\end{aligned}}$

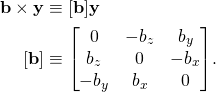
The inertia matrix is constructed by considering the angular momentum, with the reference point

R

of the body chosen to be the centre of mass

C

:^[3]^[6]

$\displaystyle {\begin{aligned}\mathbf {L} &=\left(\sum _{i=1}^{n}m_{i}\,\Delta \mathbf {r} _{i}\times \mathbf {v} _{i}\right)\\&=\left(\sum _{i=1}^{n}m_{i}\,\Delta \mathbf {r} _{i}\times \left({\boldsymbol {\omega }}\times \Delta \mathbf {r} _{i}+\mathbf {V} _{\mathbf {R} }\right)\right)\\&=\left(-\sum _{i=1}^{n}m_{i}\,\Delta \mathbf {r} _{i}\times \left(\Delta \mathbf {r} _{i}\times {\boldsymbol {\omega }}\right)\right)+\left(\sum _{i=1}^{n}m_{i}\,\Delta \mathbf {r} _{i}\times \mathbf {V} _{\mathbf {R} }\right),\end{aligned}}$

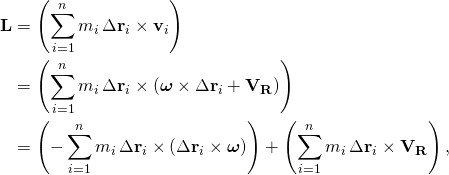
where the terms containing

V R

(

= C

) sum to zero by the definition of centre of mass.

Then, the skew-symmetric matrix $[Δ r i]$ obtained from the relative position vector $Δ r i = r i - C$ , can be used to define,

$\displaystyle \mathbf {L} =\left(-\sum _{i=1}^{n}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right){\boldsymbol {\omega }}=\mathbf {I} _{\mathbf {C} }{\boldsymbol {\omega }},$

where

I C

defined by

$\displaystyle \mathbf {I} _{\mathbf {C} }=-\left(\sum _{i=1}^{n}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right),$

is the symmetric inertia matrix of the rigid system of particles measured relative to the centre of mass

C

Kinetic energy

The kinetic energy of a rigid system of particles can be formulated in terms of the centre of mass and a matrix of mass moments of inertia of the system. Let the system of particles $P i, i = 1, \dots, n$ be located at the coordinates $r i$ with velocities $v i$ , then the kinetic energy is^[3]^[6]

$\displaystyle E_{\text{K}}={\frac {1}{2}}\left(\sum _{i=1}^{n}m_{i}\mathbf {v} _{i}\cdot \mathbf {v} _{i}\right)={\frac {1}{2}}\left(\sum _{i=1}^{n}m_{i}\left({\boldsymbol {\omega }}\times \Delta \mathbf {r} _{i}+\mathbf {V} _{\mathbf {C} }\right)\cdot \left({\boldsymbol {\omega }}\times \Delta \mathbf {r} _{i}+\mathbf {V} _{\mathbf {C} }\right)\right),$

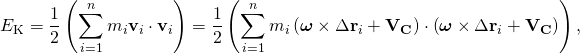
where

Δ r i = r i - C

is the position vector of a particle relative to the centre of mass.

This equation expands to yield three terms

$\displaystyle E_{\text{K}}={\frac {1}{2}}\left(\sum _{i=1}^{n}m_{i}\left({\boldsymbol {\omega }}\times \Delta \mathbf {r} _{i}\right)\cdot \left({\boldsymbol {\omega }}\times \Delta \mathbf {r} _{i}\right)\right)+\left(\sum _{i=1}^{n}m_{i}\mathbf {V} _{\mathbf {C} }\cdot \left({\boldsymbol {\omega }}\times \Delta \mathbf {r} _{i}\right)\right)+{\frac {1}{2}}\left(\sum _{i=1}^{n}m_{i}\mathbf {V} _{\mathbf {C} }\cdot \mathbf {V} _{\mathbf {C} }\right).$

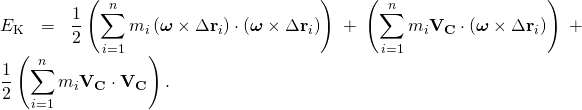
The second term in this equation is zero because

C

is the centre of mass. Introduce the skew-symmetric matrix

[Δ r i]

so the kinetic energy becomes

$\displaystyle {\begin{aligned}E_{\text{K}}&={\frac {1}{2}}\left(\sum _{i=1}^{n}m_{i}\left(\left[\Delta \mathbf {r} _{i}\right]{\boldsymbol {\omega }}\right)\cdot \left(\left[\Delta \mathbf {r} _{i}\right]{\boldsymbol {\omega }}\right)\right)+{\frac {1}{2}}\left(\sum _{i=1}^{n}m_{i}\right)\mathbf {V} _{\mathbf {C} }\cdot \mathbf {V} _{\mathbf {C} }\\&={\frac {1}{2}}\left(\sum _{i=1}^{n}m_{i}\left({\boldsymbol {\omega }}^{\mathsf {T}}\left[\Delta \mathbf {r} _{i}\right]^{\mathsf {T}}\left[\Delta \mathbf {r} _{i}\right]{\boldsymbol {\omega }}\right)\right)+{\frac {1}{2}}\left(\sum _{i=1}^{n}m_{i}\right)\mathbf {V} _{\mathbf {C} }\cdot \mathbf {V} _{\mathbf {C} }\\&={\frac {1}{2}}{\boldsymbol {\omega }}\cdot \left(-\sum _{i=1}^{n}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right){\boldsymbol {\omega }}+{\frac {1}{2}}\left(\sum _{i=1}^{n}m_{i}\right)\mathbf {V} _{\mathbf {C} }\cdot \mathbf {V} _{\mathbf {C} }.\end{aligned}}$

Thus, the kinetic energy of the rigid system of particles is given by

$\displaystyle E_{\text{K}}={\frac {1}{2}}{\boldsymbol {\omega }}\cdot \mathbf {I} _{\mathbf {C} }{\boldsymbol {\omega }}+{\frac {1}{2}}M\mathbf {V} _{\mathbf {C} }^{2}.$

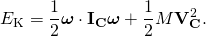
where

I C

is the inertia matrix relative to the centre of mass and

M

is the total mass.

Resultant torque

The inertia matrix appears in the application of Newton’s second law to a rigid assembly of particles. The resultant torque on this system is,^[3]^[6]

$\displaystyle {\boldsymbol {\tau }}=\left(\sum _{i=1}^{n}\left(\mathbf {r_{i}} -\mathbf {R} \right)\times m_{i}\mathbf {a} _{i}\right),$

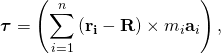
where

a i

is the acceleration of the particle

P i

. The kinematics of a rigid body yields the formula for the acceleration of the particle

P i

in terms of the position

R

and acceleration

A r

of the reference point, as well as the angular velocity vector ω and angular acceleration vector α of the rigid system as,

$\displaystyle \mathbf {a} _{i}={\boldsymbol {\alpha }}\times \left(\mathbf {r} _{i}-\mathbf {R} \right)+{\boldsymbol {\omega }}\times {\boldsymbol {\omega }}\times \left(\mathbf {r} _{i}-\mathbf {R} \right)+\mathbf {A} _{\mathbf {R} }.$

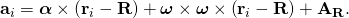
Use the centre of mass

C

as the reference point, and introduce the skew-symmetric matrix

[Δ r i] = [r i - C]

to represent the cross product

(r i - C) \times

, to obtain

$\displaystyle {\boldsymbol {\tau }}=\left(-\sum _{i=1}^{n}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right){\boldsymbol {\alpha }}+{\boldsymbol {\omega }}\times \left(-\sum _{i=1}^{n}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right){\boldsymbol {\omega }}$

The calculation uses the identity

$\displaystyle \Delta \mathbf {r} _{i}\times \left({\boldsymbol {\omega }}\times \left({\boldsymbol {\omega }}\times \Delta \mathbf {r} _{i}\right)\right)+{\boldsymbol {\omega }}\times \left(\left({\boldsymbol {\omega }}\times \Delta \mathbf {r} _{i}\right)\times \Delta \mathbf {r} _{i}\right)=0,$

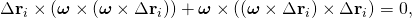
obtained from the Jacobi identity for the triple cross product as shown in the proof below:

[show]Proof

Thus, the resultant torque on the rigid system of particles is given by

$\displaystyle {\boldsymbol {\tau }}=\mathbf {I} _{\mathbf {C} }{\boldsymbol {\alpha }}+{\boldsymbol {\omega }}\times \mathbf {I} _{\mathbf {C} }{\boldsymbol {\omega }},$

where

I C

is the inertia matrix relative to the centre of mass.

Parallel axis theorem

The inertia matrix of a body depends on the choice of the reference point. There is a useful relationship between the inertia matrix relative to the centre of mass $C$ and the inertia matrix relative to another point $R$ . This relationship is called the parallel axis theorem.^[3]^[6]

Consider the inertia matrix $I R$ obtained for a rigid system of particles measured relative to a reference point $R$ , given by

$\displaystyle \mathbf {I} _{\mathbf {R} }=-\left(\sum _{i=1}^{n}m_{i}\left[\mathbf {r} _{i}-\mathbf {R} \right]^{2}\right).$

Let

C

be the centre of mass of the rigid system, then

$\displaystyle \mathbf {R} =(\mathbf {R} -\mathbf {C} )+\mathbf {C} =\mathbf {d} +\mathbf {C} ,$

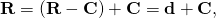
where

d

is the vector from the centre of mass

C

to the reference point

R

. Use this equation to compute the inertia matrix,

$\displaystyle \mathbf {I} _{\mathbf {R} }=-\left(\sum _{i=1}^{n}m_{i}[\mathbf {r} _{i}-\left(\mathbf {C} +\mathbf {d} \right)]^{2}\right)=-\left(\sum _{i=1}^{n}m_{i}[\left(\mathbf {r} _{i}-\mathbf {C} \right)-\mathbf {d} ]^{2}\right).$

Distribute over the cross product to obtain

$\displaystyle \mathbf {I} _{\mathbf {R} }=-\left(\sum _{i=1}^{n}m_{i}[\mathbf {r} _{i}-\mathbf {C} ]^{2}\right)+\left(\sum _{i=1}^{n}m_{i}[\mathbf {r} _{i}-\mathbf {C} ]\right)[\mathbf {d} ]+[\mathbf {d} ]\left(\sum _{i=1}^{n}m_{i}[\mathbf {r} _{i}-\mathbf {C} ]\right)-\left(\sum _{i=1}^{n}m_{i}\right)[\mathbf {d} ]^{2}.$

The first term is the inertia matrix

I C

relative to the centre of mass. The second and third terms are zero by definition of the centre of mass

C

. And the last term is the total mass of the system multiplied by the square of the skew-symmetric matrix

[d]

constructed from

d

The result is the parallel axis theorem,

$\displaystyle \mathbf {I} _{\mathbf {R} }=\mathbf {I} _{\mathbf {C} }-M[\mathbf {d} ]^{2},$

where

d

is the vector from the centre of mass

C

to the reference point

R

Note on the minus sign: By using the skew symmetric matrix of position vectors relative to the reference point, the inertia matrix of each particle has the form $- m [r] 2$ , which is similar to the $mr 2$ that appears in planar movement. However, to make this to work out correctly a minus sign is needed. This minus sign can be absorbed into the term $m [r] T [r]$ , if desired, by using the skew-symmetry property of $[r]$ .

Scalar moment of inertia in a plane

The scalar moment of inertia, $I L$ , of a body about a specified axis whose direction is specified by the unit vector $k̂$ and passes through the body at a point $R$ is as follows:^[6]

$\displaystyle I_{L}=\mathbf {\hat {k}} \cdot \left(-\sum _{i=1}^{N}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right)\mathbf {\hat {k}} =\mathbf {\hat {k}} \cdot \mathbf {I} _{\mathbf {R} }\mathbf {\hat {k}} =\mathbf {\hat {k}} ^{\mathsf {T}}\mathbf {I} _{\mathbf {R} }\mathbf {\hat {k}} ,$

where

I R

is the moment of inertia matrix of the system relative to the reference point

R

, and

[Δ r i]

is the skew symmetric matrix obtained from the vector

Δ r i = r i - R

This is derived as follows. Let a rigid assembly of $N$ particles, $P i, i = 1, \dots, N$ , have coordinates $r i$ . Choose $R$ as a reference point and compute the moment of inertia around a line L defined by the unit vector $k̂$ through the reference point $R$ , $L (t) = R + t k̂$ . The perpendicular vector from this line to the particle $P i$ is obtained from $Δ r i$ by removing the component that projects onto $k̂$ .

$\displaystyle \Delta \mathbf {r} _{i}^{\perp }=\Delta \mathbf {r} _{i}-\left(\mathbf {\hat {k}} \cdot \Delta \mathbf {r} _{i}\right)\mathbf {\hat {k}} =\left(\mathbf {E} -\mathbf {\hat {k}} \mathbf {\hat {k}} ^{\mathsf {T}}\right)\Delta \mathbf {r} _{i},$

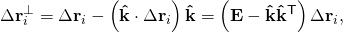
where

E

is the identity matrix, so as to avoid confusion with the inertia matrix, and

k̂ k̂ T

is the outer product matrix formed from the unit vector

k̂

along the line

L

To relate this scalar moment of inertia to the inertia matrix of the body, introduce the skew-symmetric matrix $[k̂]$ such that $[k̂] y = k̂ \times y$ , then we have the identity

$\displaystyle -\left[\mathbf {\hat {k}} \right]^{2}\equiv \left|\mathbf {\hat {k}} \right|^{2}\left(\mathbf {E} -\mathbf {\hat {k}} \mathbf {\hat {k}} ^{\mathsf {T}}\right)=\mathbf {E} -\mathbf {\hat {k}} \mathbf {\hat {k}} ^{\mathsf {T}},$

noting that

k̂

is a unit vector.

The magnitude squared of the perpendicular vector is

$\displaystyle {\begin{aligned}\left|\Delta \mathbf {r} _{i}^{\perp }\right|^{2}&=\left(-\left[\mathbf {\hat {k}} \right]^{2}\Delta \mathbf {r} _{i}\right)\cdot \left(-\left[\mathbf {\hat {k}} \right]^{2}\Delta \mathbf {r} _{i}\right)\\&=\left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\cdot \left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\end{aligned}}$

The simplification of this equation uses the triple scalar product identity

$\displaystyle \left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\cdot \left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\equiv \left(\left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\times \mathbf {\hat {k}} \right)\cdot \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right),$

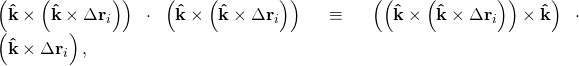
where the dot and the cross products have been interchanged. Exchanging products, and simplifying by noting that

Δ r i

and

k̂

are orthogonal:

$\displaystyle {\begin{aligned}&\left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\cdot \left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\\={}&\left(\left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\times \mathbf {\hat {k}} \right)\cdot \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\\={}&\left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\cdot \left(-\Delta \mathbf {r} _{i}\times \mathbf {\hat {k}} \right)\\={}&-\mathbf {\hat {k}} \cdot \left(\Delta \mathbf {r} _{i}\times \Delta \mathbf {r} _{i}\times \mathbf {\hat {k}} \right)\\={}&-\mathbf {\hat {k}} \cdot \left[\Delta \mathbf {r} _{i}\right]^{2}\mathbf {\hat {k}} .\end{aligned}}$

Thus, the moment of inertia around the line

L

through

R

in the direction

k̂

is obtained from the calculation

$\displaystyle {\begin{aligned}I_{L}&=\left(\sum _{i=1}^{N}m_{i}\left|\Delta \mathbf {r} _{i}^{\perp }\right|^{2}\right)\\&=\left(-\sum _{i=1}^{N}m_{i}\mathbf {\hat {k}} \cdot \left[\Delta \mathbf {r} _{i}\right]^{2}\mathbf {\hat {k}} \right)=\mathbf {\hat {k}} \cdot \left(-\sum _{i=1}^{N}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right)\mathbf {\hat {k}} \\&=\mathbf {\hat {k}} \cdot \mathbf {I} _{\mathbf {R} }\mathbf {\hat {k}} =\mathbf {\hat {k}} ^{\mathsf {T}}\mathbf {I} _{\mathbf {R} }\mathbf {\hat {k}} ,\end{aligned}}$