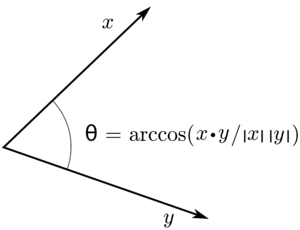
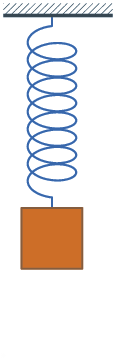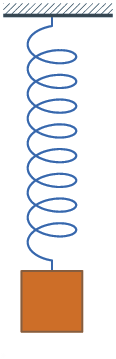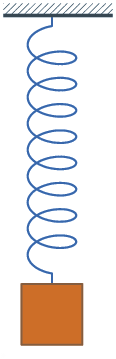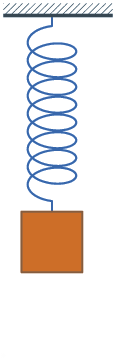
從『簡諧振子』︰
來自於美國科羅拉多大學的 PhET Physics Education Technology 計劃,免費提供以樂趣、互動與研究為基礎的物理現象模擬軟體。這一個計畫是由二零零二年美國諾貝爾物理學獎得主之一的卡爾‧埃德溫‧威曼 Carl Edwin Wieman 所發起,根據 WiKi 上所載
began with Wieman’s vision to improve the way science is taught and learned. Their stated mission is “To advance science and math literacy and education worldwide through free interactive simulations.”
,按照現今官網的說明
PhET provides fun, interactive, research-based simulations of physical phenomena for free. We believe that our research-based approach- incorporating findings from prior research and our own testing- enables students to make connections between real-life phenomena and the underlying science, deepening their understanding and appreciation of the physical world.
…
目前它的線上內容早已經括及多類科學領域,並且很多內容也有了中文的翻譯網頁。作者認為如何用計算機輔助『教育』與『學習』正是今日當有之重要的『學習工具』,實現人們可以用『科學』來解釋『日常生活』中所經驗到的種種『自然現象』的教育宗旨。當你閱讀本文看到有『點擊啟動』的圖片時,請在『點擊啟動』的方形區域外,使用『滑鼠左鍵』點擊圖片的任何位置,進入嵌入式『PhET』線上模擬器的軟體世界。
一 個諧振子 harmonic oscillator 是一個物理系統,當它從平衡位置發生位移時,會受到一個正比於位移量 ![]() 的恢復力
的恢復力 ![]() ── 虎克定律──︰
── 虎克定律──︰![]() ,其中
,其中 ![]() 是一個正值常數。假使這個系統不受其它的外力影響,通常稱作『簡諧振子』Simple harmonic oscillator;如果此系統同時遭受到與速度成正比的『摩擦力』
是一個正值常數。假使這個系統不受其它的外力影響,通常稱作『簡諧振子』Simple harmonic oscillator;如果此系統同時遭受到與速度成正比的『摩擦力』 ![]() ,一般叫做『阻尼振子』Damped harmonic oscillator;要是這個系統還有著跟時間相關的外力
,一般叫做『阻尼振子』Damped harmonic oscillator;要是這個系統還有著跟時間相關的外力 ![]() 的作用,那麼就稱之為『受驅振子』Driven harmonic oscillators。
的作用,那麼就稱之為『受驅振子』Driven harmonic oscillators。
依據牛頓第二運動定律,一個簡諧振子的方程式為
![]() ,它的解是
,它的解是
![]() ,此處
,此處 ![]() 是『相位角』,
是『相位角』,
![]() ,式中
,式中 ![]() 是『角頻率』,
是『角頻率』,![]() 是『周期』。
是『周期』。
也就是說簡諧振子是一種『頻率』為 ![]() ,『振幅』為
,『振幅』為 ![]() 的週期運動。假設
的週期運動。假設 ![]() 的初始時,
的初始時,![]() ,得到
,得到
![]()
![]()
動能 = ![]() ,位能=
,位能=![]() ,系統總能量
,系統總能量
![]()
由此可以知道簡諧振子的系統總能量是一個常數,這稱之為『能量守恆量』定律,它和『振幅』的平方成正比。它的『頻率』![]() 只依賴於系統『固有』的
只依賴於系統『固有』的 ![]() 與
與 ![]() ,也是一個不變的常量。
,也是一個不變的常量。
─── 摘自《【Sonic π】聲波之傳播原理︰振動篇》
到『駐波形成』︰
在一輛長列『左行』的火車上有一個很長的『水槽』,上有一向右的『行進波』
![]()
,假使向左的火車與向右之水波速度相同,那麼一位站在月台的『觀察者』 將如何描述那個『行進波』的呢?
如果觀察水由水龍頭注入水槽的現象,由於水在到達槽底前的流速『較快』,然而到達槽底後水的流速突然的『變慢』,因此會發生『水躍』Hydraulic jump 的現象,此時水之部份動能將轉換為位能,故而在槽底的液面形成『駐波』。這個現象在『河水』的『流速』突然『由快變慢』時也可能發生,因而有人能在『河裡衝浪』,他正站在『駐波』之上!!
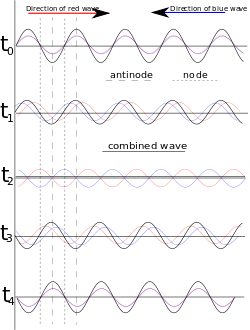
那什麼是『駐波』的呢?比方說一個『不動的』stationary 介質中,向左的波 ![]() 與向右的波
與向右的波 ![]() 疊加後的『合成波』
疊加後的『合成波』![]() ,在『特定』的『邊界條件』下,被『侷限』在一定『空間區域』內無法前進,因此稱為『駐波』。由於駐波不能傳播能量,它的能量將『儲存』在那個空間區域裡。駐波所在區域,『振幅為零』的點稱為『節點』或『波節』Node ,『振幅最大』的點位於兩『節點』之間,通常叫做『腹點』或『波腹』Antinode。
,在『特定』的『邊界條件』下,被『侷限』在一定『空間區域』內無法前進,因此稱為『駐波』。由於駐波不能傳播能量,它的能量將『儲存』在那個空間區域裡。駐波所在區域,『振幅為零』的點稱為『節點』或『波節』Node ,『振幅最大』的點位於兩『節點』之間,通常叫做『腹點』或『波腹』Antinode。
一根長度 ![]() 震盪的弦上,一個向右的簡諧波
震盪的弦上,一個向右的簡諧波 ![]() ,由於弦的兩頭固定,那個波在右端點也只能『反射』回來,形成了
,由於弦的兩頭固定,那個波在右端點也只能『反射』回來,形成了 ![]() ,此時合成波
,此時合成波 ![]() 是
是
![]()
,可用三角恆等式簡化為
![]()
。此時『時間項』與『空間項』分離,形成『駐波』。在 ![]() 時,
時,![]() ,此處
,此處 ![]() 是整數,這就是『節點』;當
是整數,這就是『節點』;當 ![]() 時
時 ![]() ,也就是『腹點』。當然波長
,也就是『腹點』。當然波長 ![]() 就得滿足
就得滿足 ![]() 的邊界條件。
的邊界條件。
─── 琴弦擇音而振, 苟非知音焉得共鳴。───
─── 摘自《【Sonic π】聲波之傳播原理︰原理篇《四下》》
我們介紹了聲波的物理現象和模型以及數學推導。
假使讀者浸潤思考所謂『行進波』之『歷時形貌』︰
假使從『因次分析』的觀點來看,向右波形 ![]() 中
中 ![]() 的因次是『長度』,因此『通用解』的寫法恐非是適切的『物理表達式』。由於一個波的『頻率』
的因次是『長度』,因此『通用解』的寫法恐非是適切的『物理表達式』。由於一個波的『頻率』 ![]() 、『波長』
、『波長』 ![]() 和『速度』
和『速度』![]() 有一定的關係式︰
有一定的關係式︰![]() 。如果參考『單擺系統』的『時間』用『單擺週期』
。如果參考『單擺系統』的『時間』用『單擺週期』 ![]() 來度量,是一個『無因次純量』
來度量,是一個『無因次純量』![]() ,那麼很自然的一個物理系統『空間』之『度量』,也應當用著該系統中的『長度物理量』,在此也就是那個波的『波長』
,那麼很自然的一個物理系統『空間』之『度量』,也應當用著該系統中的『長度物理量』,在此也就是那個波的『波長』 ![]() 來表達,
來表達,![]() 也是『無因次純量』。這樣向右波形就可以改寫成
也是『無因次純量』。這樣向右波形就可以改寫成
![]() 。
。
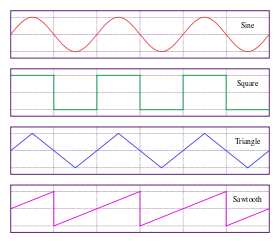
左圖是一些常見的波形,也就是 ![]() 對於相位
對於相位 ![]() 的『函數圖形』。假使從『時刻』
的『函數圖形』。假使從『時刻』![]() 來觀看,
來觀看,![]() ,此處
,此處 ![]() ,就是此波的整體『空間樣態』。如果在『位置』
,就是此波的整體『空間樣態』。如果在『位置』 ![]() 作時察,
作時察, ![]() ,此時
,此時 ![]() ,也就是此波此處的『歷時形貌』,這就是一個波之『相位』的『時空觀』。因此更可以了解惠更斯所說『波前』的物理意義是以『時間』為軸,來描述波的『空間樣態』到底會如何『隨時變化』。
,也就是此波此處的『歷時形貌』,這就是一個波之『相位』的『時空觀』。因此更可以了解惠更斯所說『波前』的物理意義是以『時間』為軸,來描述波的『空間樣態』到底會如何『隨時變化』。
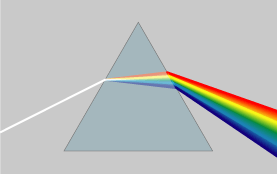
光的『色散現象』說明不同『頻率』的波,在一個『介質』裡傳播的『速度』可以不同,也就是說它們的『波長』不一樣。通常用色散關係
![]()
表示。此處的 ![]() 就是『波數』
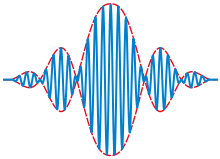
就是『波數』![]() 的『波速函數』。假使一個『波形』是由多個『頻率』組成,在『色散介質』中傳播,長時間來看大概很難『保形』的了。短時間的觀點來說,我們講那個『波包』wave packet 整體用著
的『波速函數』。假使一個『波形』是由多個『頻率』組成,在『色散介質』中傳播,長時間來看大概很難『保形』的了。短時間的觀點來說,我們講那個『波包』wave packet 整體用著 ![]() 的群速度在變化。左圖是深水『表面重力』波,圖中用著『紅點』表示『相速度』,以及『綠點』表示『群速度』。
的群速度在變化。左圖是深水『表面重力』波,圖中用著『紅點』表示『相速度』,以及『綠點』表示『群速度』。
或曾想聽覺研究乙事,尚未足乎?
Hearing
Hearing, or auditory perception, is the ability to perceive sound by detecting vibrations,[1] changes in the pressure of the surrounding medium through time, through an organ such as the ear.
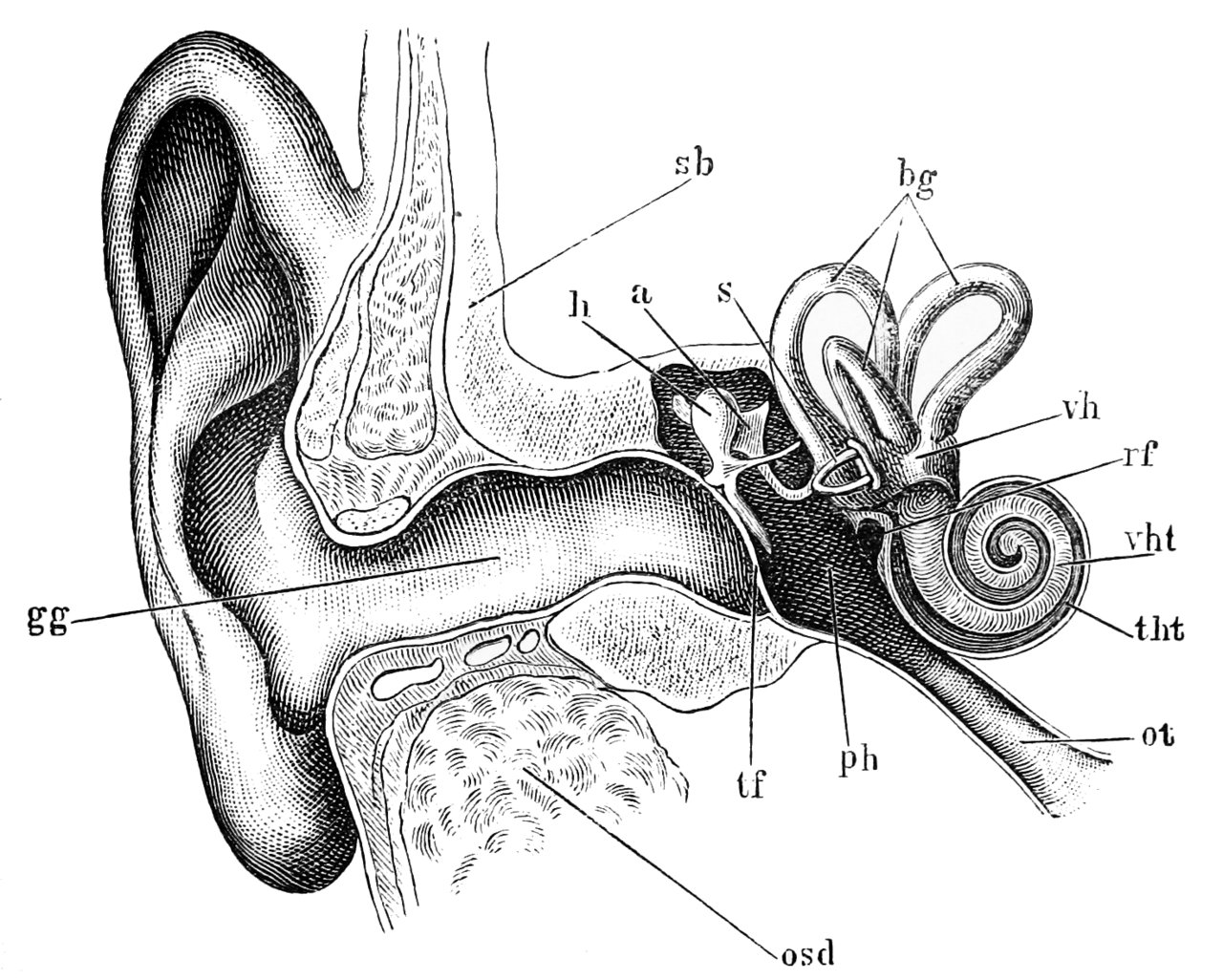
Schematic diagram of the human ear
……
Mathematics
The basilar membrane of the inner ear spreads out different frequencies: high frequencies produce a large vibration at the end near the middle ear (the “base”), and low frequencies a large vibration at the distant end (the “apex”). Thus the ear performs a sort of frequency analysis, roughly similar to a Fourier transform.[16][17] However, the nerve pulses delivered to the brain contain both rate-versus-place and fine temporal structure information, so the similarity is not strong.
………
耳的頻率響應
耳感受聲音的靈敏度與頻率的關係。外耳道的共振特性、中耳聲阻抗的頻率特性、耳蝸內行波的機械特性、螺旋器結構的濾波特性及感受細胞的生理特性,共 同決定了耳對不同頻率的聲音感受的靈敏度是不一樣的。各種動物都有其聽覺較靈敏的頻率範圍,人類大致是1000~8000赫,在這一範圍以外靈敏度依次遞 減。
聽覺機制
包括:機械→電→化學→神經衝動→中樞信息處理等一串過程。在蝸管的內淋巴液中若以鼓階的外淋巴中的電位為零通常有+80毫伏的正電位,螺旋器毛細 胞內的電位則約為-60毫伏,電流不斷從蝸管通過蓋膜、毛細胞的纖毛、細胞膜及周圍組織流入毛細胞內,形成迴路。當聲音引起基底膜運動時,螺旋器也隨之作 相應的運動。由於運動的方向、慣性等因素的作用,毛細膜與蓋膜之間產生一種展力使纖毛彎曲,改變了迴路中的電阻,從而調製了通過的電流,使聽神經末梢和毛 細胞間形成的突觸周圍也有相應的電位變化,導致化學遞質的釋放,後者使神經末梢興奮,發出神經衝動。接受各種不同特性的聲音後發放出的神經衝動在時間(不 同的節律)和空間(不同的神經纖維)上各有不同的構型,它們攜帶有關聲音的信息,依次傳至各級聽覺中樞,經過處理分析,最後便產生反映聲音各種複雜特性的 聽覺。有關信息在聽覺中樞的處理過程還不完全清楚。
聽覺學說
對聲音的頻率如何在耳蝸進行分析曾提出過多種假設,但基本上可概括為兩種觀點:①不同頻率的聲音興奮基底膜不同部位的感受細胞,興奮部位是頻率分析 的依據,有關頻率的信息以衝動發放的空間構型來傳送;②不同頻率的聲音使聽神經興奮後發出不同頻率的衝動,衝動頻率是聲音頻率分析的依據,有關信息以衝動 發放的時間構型來傳送。前一觀點叫做部位機制,後一觀點叫做時間機制,兩觀點不是互相排斥,而是互相補充的。各種學說的一個共同缺點是只著眼於耳蝸,而頻 率精確分析的機制是不能脫離中樞,單在耳蝸水平上尋找的。
行波學說
聲音引起基底膜的波動是一種行波,從耳蝸基部開始逐步向蝸頂移動,在移動過程中行波的振幅是變化的,振幅最大點的位置及行波移動的距離都隨聲音的頻 率而變,振幅最大點在高頻刺激時靠近耳蝸基部,頻率逐漸降低時它逐漸向蝸頂移動,行波振幅最大處基底膜受刺激最強,其位置與頻率的關係是耳蝸頻率分析的基 礎。行波理論正確描述了500Hz以上的聲音引起的基底膜活動,但難以解釋500Hz以下的聲音對基底膜的影響。
頻率學說
聽神經不同的纖維受刺激後發出的神經衝動可以在時間上錯開,分別與聲波不同的周期同步,每一聲波周期因而都可以有一定數量的纖維同步發放,叫做排 放。總體上排放的頻率便與聲音頻率一致,形成聽覺頻率分析的依據。在聽神經纖維上記錄神經衝動的實驗表明,神經衝動不一定是每一聲波周期都發放一次,高頻 時一般要隔若干周期才發放一次,但發放的時間總是和聲波周期的相位保持良好的同步關係(鎖相關係),說明衝動排放的組成是具備必要條件的。但頻率理論難以 解釋人而對聲音頻率的分析。因為基底膜無法做每秒1000次以上的快速運動。這是和人耳能夠接受超過1000Hz以上的聲音不符合的。
共鳴學說
赫爾姆霍茲認為基底膜的橫纖維能夠對不同頻率的聲音產生共鳴。高頻聲音誘發短纖維共鳴,低頻誘髮長纖維共鳴。由於強調了基底膜的震動部位對產生音調聽覺的作用,因為也叫位置理論。
神經齊射學說
當聲音頻率低於400Hz時,聽神經個別纖維的發放頻率是和聲音頻率對應的。聲音頻率提高時,個別纖維利用聯合齊射反應頻率較高的聲音。韋弗爾指 出,用神經齊射理論可以對5000Hz以下的聲音進行頻率分析。聲音頻率超過5000Hz,位置理論是對頻率進行編碼的唯一基礎。
聲音的強度分析
感受細胞和神經單元的興奮閾值有高有低,刺激強時被興奮的感受細胞和神經單元便多,每一神經單元興奮後發放神經衝動的數目也多。對於聽覺,被興奮單 元的閾值是高還是低,興奮單元數目的多少,以及神經衝動數目的多少,這都可以是聲音強度分析的依據。按照排放學說,興奮單元數目及發放衝動數目的增加,僅 使組成每一排放的發放纖維數目增加,而並不增加排放的數目,因此與頻率分析不矛盾。
聲源定位
有賴於雙耳聽覺。由於從聲源到兩耳的距離不同及聲音傳播途中障礙物的不同,從某一方位發出的聲音到達兩耳時便有時間(或相位)差和強度差,其大小與 聲源的方位有關。在同一瞬間雙耳接受到聲音的時間差是低頻聲定位的主要依據,強度差是高頻聲定位的主要依據,耳廓的聚聲作用對高頻聲定位也有一定的幫助。
───
深化了解
In performance, musicians convert sheet music representations into sound which is transmitted through the air as air pressure oscillations. In essence, sound is simply air vibrating (Wikipedia). Sound vibrates through the air as longitudinal waves, i.e. the oscillations are parallel to the direction of propagation.
Audio refers to the production, transmission, or reception of sounds that are audible by humans. An audio signal is a representation of sound that represents the fluctuation in air pressure caused by the vibration as a function of time. Unlike sheet music or symbolic representations, audio representations encode everything that is necessary to reproduce an acoustic realization of a piece of music. However, note parameters such as onsets, durations, and pitches are not encoded explicitly. This makes converting from an audio representation to a symbolic representation a difficult and ill-defined task.
耶!







.png)