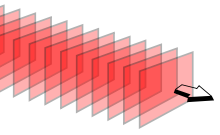
我們已經知道,在物理上『波』是『空間』或者『物質』中『擾動』的『傳播現象』。它在傳播時『波前』將『能量』由此處帶往彼處,通常『波』即使需要透過『介質』傳播,構成那個介質的『物質粒子』在『波前通過時』並不會產生『永久性位移』之變化,也不會一併跟著『波前前進』發生了『物質傳送』的現象。假使說將『波前』想像成空間『擾動式樣』,分布在『介質』的『空間』裡,那麼『波前』在『時間』中行徑之『變化』,也就是『波傳播』的『時空圖像』了。自然界各種不同類型的『波』,不論它是『機械的』還是『非機械的』都可以由廣義的『波動方程式』來描述,然而『具體現象』之『□□波』的『數學形式』,卻是各有各的不同。
一個『振動』的『音叉』因為與『周遭空氣』的碰撞傳遞『能量』給空氣中的某些『分子』,然後這些分子又去碰撞『周遭另一些分子』將『振動』漸次依時傳遞下去。然而在『傳遞振動』時,先時碰撞之『所得』將為此時碰撞之『所失』,因此『空氣分子』並不會因為『傳播聲音』就跟著聲音『一塊跑了』!!
一七一七年出生的讓‧勒朗‧達朗貝爾 Jean le Rond D’Alembert,是法國的物理學家、數學家和天文學家。他的身世非常可憐,是某位『作家』與一個『騎士』的私生子,出生後即被遺棄在巴黎的一座名為聖‧讓‧勒‧朗 Saint Jean-le-Rond 之教堂附近,故依習俗以教堂的名字取名,後為一位『玻璃匠』收養長大成人。達朗貝爾的一生在很多學科領域裡進行研究,於數學、力學、天文學、哲學、音樂和社會活動方面都有很多的建樹。一生六十六年間,著有八卷巨著《數學手冊》、力學專著《動力學》、二十三卷的《文集》以及《百科全書》的序言。他的很多的研究成果記載於《宇宙體系的幾個要點研究》中。一七四七年達朗貝爾發表了《Recherches sur la courbe que forme une corde tenduë mise en vibration》Researches on the curve that a tense cord forms [when] set into vibration 的論文;由於他的貢獻,其後之人將『一維波動方程式』以及它的『通用解』general solution 稱之為『達朗貝爾公式』d’Alembert’s formula。
如果說一個『擾動』可以數學上描述為 ![]() ,這是講在
,這是講在 ![]() 時刻,這個擾動的『振幅』
時刻,這個擾動的『振幅』![]() 在
在 ![]() 所構成的座標系上看是一條『波前曲線』。假使這個波前沿著
所構成的座標系上看是一條『波前曲線』。假使這個波前沿著 ![]() 軸『向右』以速度
軸『向右』以速度 ![]() 『保形』等速傳播,那麼
『保形』等速傳播,那麼 ![]() 時刻時,這條曲線就可以用
時刻時,這條曲線就可以用 ![]() 來描述。同樣的如果這個波前沿著
來描述。同樣的如果這個波前沿著 ![]() 軸『向左』以速度
軸『向左』以速度 ![]() 『保形』等速傳播,那麼
『保形』等速傳播,那麼 ![]() 時刻時,這條曲線也可以用
時刻時,這條曲線也可以用 ![]() 來描述。如此這個保形的擾動
來描述。如此這個保形的擾動 ![]() 會滿足
會滿足
![]() 偏微分方程式。
偏微分方程式。
這就將我們帶進了所謂的『一維波動方程式』。由此來推測這個『偏微分方程式』的『通用解』將可以表示為:
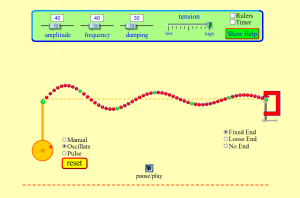
在 x 軸上一個向左傳播的波和一個向右傳播的波的疊加。
在數學的描述上,一維波動方程式定義為︰
![]()
![]() 。
。
前面所講的『波前保形』傳播想法,舉例來說它可以是一個『平面波』在『均勻介質』中的傳播,或者說是某種『自然』或『人為』的『線型水面波』 。大自然中的『現象』有時會『指引』數學上『求解』的『方向』,因為終究人們能夠發現的那個現象方程式,也是來自於『大自然』的啊!!難到一個不受外物影響的『波前』它在 ![]() 時刻的『相同相位』──
時刻的『相同相位』── ![]() ── 之點,到了
── 之點,到了 ![]() 時刻就會變成不一樣的嗎??
時刻就會變成不一樣的嗎??
因此物理上的『直覺』,建議著數學上的『變數變換』![]()
,這樣那個方程式就變成了
![]() ,因此
,因此
![]()
,此處的 ![]() 就是『向左』與『向右』的波,一個與
就是『向左』與『向右』的波,一個與 ![]() 有關的『待解』函數,從初始條件可得
有關的『待解』函數,從初始條件可得
![]()
![]()
『求解』再變換回 ![]() 後就得到了達朗貝爾公式
後就得到了達朗貝爾公式
![]()
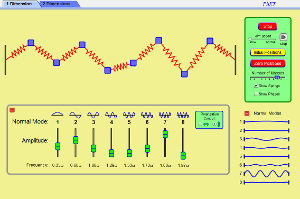
為了闡明『波』的傳播與簡諧振子『振動』的密切關係,就讓我們考慮一個由『彈簧與質點』所構成的『彈簧鏈模型』物理系統︰
有 ![]() 個質點 ── 它的大小不計,假設比
個質點 ── 它的大小不計,假設比 ![]() 小很多 ── 以間隔
小很多 ── 以間隔 ![]() 均勻的安置在總長度為
均勻的安置在總長度為 ![]() 的彈簧鏈 ── 它的質量不計,假設比一個質點
的彈簧鏈 ── 它的質量不計,假設比一個質點 ![]() 小很多 ── 上,此系統總質量
小很多 ── 上,此系統總質量 ![]() ,鏈的總體虎克常數為
,鏈的總體虎克常數為 ![]()
圖中 ![]() 表示位於
表示位於 ![]() 處的質點偏離平衡位置的距離。
處的質點偏離平衡位置的距離。
假使這個彈簧鏈物理系統不受其它外力作用,如果我們分析作用在位於 ![]() 處的質點
處的質點 ![]() 上的力,依據牛頓第二運動定律
上的力,依據牛頓第二運動定律
![]()
![]()
![]()
此處 ![]() 代表
代表 ![]() 處質點慣性力,而
處質點慣性力,而 ![]() 表達
表達 ![]() 處質點所受到的來自左右『鄰近』兩方的『虎克之彈簧回復力』。因此根據『動力學』中的『達朗貝爾原理』── 知名的『虛功原理』的動力學版本 ──,這個位於
處質點所受到的來自左右『鄰近』兩方的『虎克之彈簧回復力』。因此根據『動力學』中的『達朗貝爾原理』── 知名的『虛功原理』的動力學版本 ──,這個位於 ![]() 處質點的運動方程式是
處質點的運動方程式是 ![]() ,所以
,所以
![]()
它可以用整個物理系統的常量 ![]() 將上式改寫為
將上式改寫為
![]()
如果設想一條長度 ![]() 的彈簧鏈模型之極限
的彈簧鏈模型之極限 ![]() 狀況,此時
狀況,此時 ![]() ,這個物理系統將可以看成『線密度』是
,這個物理系統將可以看成『線密度』是 ![]() 的『弦』了。這個系統的波動方程式為
的『弦』了。這個系統的波動方程式為
![]()
比之於一維波動方程式,於是得到波速 ![]() 。
。
果真是此處 ![]() 一時
一時 ![]() 之『振動』
之『振動』![]() ,它要是掀起了『波瀾』
,它要是掀起了『波瀾』![]() ,就將會引起了彼處
,就將會引起了彼處 ![]() 它時之『動盪』
它時之『動盪』![]() 。易經裡講︰『震』亨。 震來虩虩,笑言啞啞。 震驚百里,不喪匕鬯。當真如此!!
。易經裡講︰『震』亨。 震來虩虩,笑言啞啞。 震驚百里,不喪匕鬯。當真如此!!
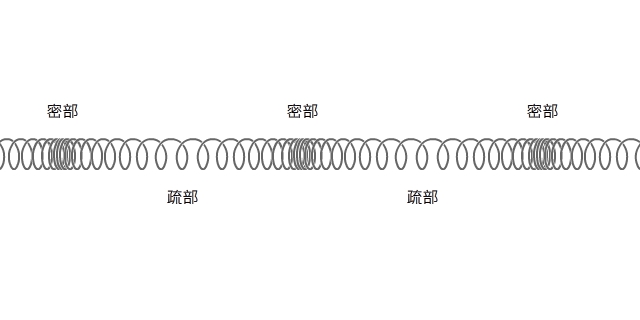
如果細思彈簧鏈模型的『波擾』![]() 的振動方向,它可以是在
的振動方向,它可以是在 ![]() 面上沿著
面上沿著 ![]() 軸的方向,形成的是一種『縱波』,常作為『聲音傳播』模型。
軸的方向,形成的是一種『縱波』,常作為『聲音傳播』模型。
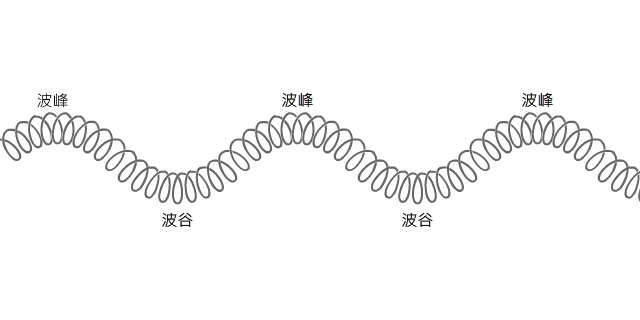
它也可以是在 ![]() 面上沿著
面上沿著 ![]() 軸的方向,就變成一種『橫波』,可當作『弦的音樂』模型。
軸的方向,就變成一種『橫波』,可當作『弦的音樂』模型。