如果我們將『受驅波動方程式』
![]()
『初始狀態』── 位移和速度 ──
![]()
![]()
![]()
,與一個質量是 ![]() 受力為
受力為 ![]() 的質點在
的質點在 ![]() 軸上的『加速度運動』
軸上的『加速度運動』
![]()
![]()
作個『項次對照』觀察之後,可以發現一個不受外力驅使的『波動傳播』,彷彿是一個『自由質點』依『初始狀態』作『慣性運動 』── 牛頓第一運動定律 ──,最主要的『差異』在於『波動』會自發的向『左右』傳播。比方講從『右向波』![]() 上看,假使一開始
上看,假使一開始 ![]() 就在『在波前』
就在『在波前』![]() 的
的 ![]() 處作記號的『點』
處作記號的『點』 ![]() ,它在
,它在 ![]() 的時刻會在
的時刻會在 ![]() 的『當下處』
的『當下處』 ![]() 之位置,也就是它們是說屬於『同一相位』
之位置,也就是它們是說屬於『同一相位』 ![]() 的『波前』,由於『波前形狀』
的『波前』,由於『波前形狀』![]() 對所有的『記號點』
對所有的『記號點』![]() 『相位相同』之點都『取值』一樣,所以可以說『右向波』是『保形的』;同理也能夠說明『左向波』
『相位相同』之點都『取值』一樣,所以可以說『右向波』是『保形的』;同理也能夠說明『左向波』 ![]() 也是『保形的』,因是之故當我們在『
也是『保形的』,因是之故當我們在『![]() 時刻』與『
時刻』與『![]() 位置』來『觀察』這個波的時候,就會得到
位置』來『觀察』這個波的時候,就會得到
![]()
。也就是說假使系統的『初始條件』使得那個波只能『向左』或者『向右』傳播,雖然在『均質無垠』不受系統外力的『介質』裡,更像是一個『勇往直前』的『保形自由波』,也難逃遇到『其他介質』時,『反射』與『折射』再度掀起『左右波瀾』。果真它是『身不由己』的嗎??
當然一個『受驅之波』相似於『受力粒子』也會產生運動的『狀態改變』,然而就算『自由粒子』也不能不受約束『無窮加速』,更別說波的『傳播速度』本就是『受限的』,故在一般情況下,這個『波的演變』可能『極其複雜』,以至於『斑駁點點』,若想要『波瀾狀闊』還是很困難的了!更別說自然界又有『處處阻力』,宛如『受驅振子』外力『停歇』後,終將歸於『靜止』。以指撥弦欲求知音或許也只能夢寐以求的哇!!
假使從『因次分析』的觀點來看,向右波形 ![]() 中
中 ![]() 的因次是『長度』,因此『通用解』的寫法恐非是適切的『物理表達式』。由於一個波的『頻率』
的因次是『長度』,因此『通用解』的寫法恐非是適切的『物理表達式』。由於一個波的『頻率』 ![]() 、『波長』
、『波長』 ![]() 和『速度』
和『速度』![]() 有一定的關係式︰
有一定的關係式︰![]() 。如果參考『單擺系統』的『時間』用『單擺週期』
。如果參考『單擺系統』的『時間』用『單擺週期』 ![]() 來度量,是一個『無因次純量』
來度量,是一個『無因次純量』![]() ,那麼很自然的一個物理系統『空間』之『度量』,也應當用著該系統中的『長度物理量』,在此也就是那個波的『波長』
,那麼很自然的一個物理系統『空間』之『度量』,也應當用著該系統中的『長度物理量』,在此也就是那個波的『波長』 ![]() 來表達,
來表達,![]() 也是『無因次純量』。這樣向右波形就可以改寫成
也是『無因次純量』。這樣向右波形就可以改寫成
![]() 。
。
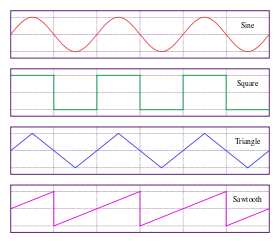
左圖是一些常見的波形,也就是 ![]() 對於相位
對於相位 ![]() 的『函數圖形』。假使從『時刻』
的『函數圖形』。假使從『時刻』![]() 來觀看,
來觀看,![]() ,此處
,此處 ![]() ,就是此波的整體『空間樣態』。如果在『位置』
,就是此波的整體『空間樣態』。如果在『位置』 ![]() 作時察,
作時察, ![]() ,此時
,此時 ![]() ,也就是此波此處的『歷時形貌』,這就是一個波之『相位』的『時空觀』。因此更可以了解惠更斯所說『波前』的物理意義是以『時間』為軸,來描述波的『空間樣態』到底會如何『隨時變化』。
,也就是此波此處的『歷時形貌』,這就是一個波之『相位』的『時空觀』。因此更可以了解惠更斯所說『波前』的物理意義是以『時間』為軸,來描述波的『空間樣態』到底會如何『隨時變化』。
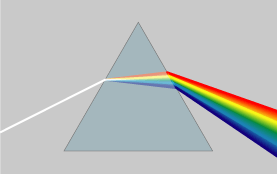
光的『色散現象』說明不同『頻率』的波,在一個『介質』裡傳播的『速度』可以不同,也就是說它們的『波長』不一樣。通常用色散關係
![]()
表示。此處的 ![]() 就是『波數』
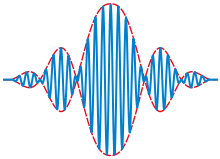
就是『波數』![]() 的『波速函數』。假使一個『波形』是由多個『頻率』組成,在『色散介質』中傳播,長時間來看大概很難『保形』的了。短時間的觀點來說,我們講那個『波包』wave packet 整體用著
的『波速函數』。假使一個『波形』是由多個『頻率』組成,在『色散介質』中傳播,長時間來看大概很難『保形』的了。短時間的觀點來說,我們講那個『波包』wave packet 整體用著 ![]() 的群速度在變化。左圖是深水『表面重力』波,圖中用著『紅點』表示『相速度』,以及『綠點』表示『群速度』。
的群速度在變化。左圖是深水『表面重力』波,圖中用著『紅點』表示『相速度』,以及『綠點』表示『群速度』。
那麼對於一個不產生色散的介質 ![]() 來講,各個頻率的成份波都跑得一樣快,這時
來講,各個頻率的成份波都跑得一樣快,這時
![]()
,也許將可以保其『形色』的了。色散現象引發了『光學系統』裡的『色差』,產生『透鏡工藝』中需要搭配不同『折射率』的『光學材料』,這是製作『好的透鏡』的重要條件之一。
在一輛長列『左行』的火車上有一個很長的『水槽』,上有一向右的『行進波』
![]()
,假使向左的火車與向右之水波速度相同,那麼一位站在月台的『觀察者』 將如何描述那個『行進波』的呢?
如果觀察水由水龍頭注入水槽的現象,由於水在到達槽底前的流速『較快』,然而到達槽底後水的流速突然的『變慢』,因此會發生『水躍』Hydraulic jump 的現象,此時水之部份動能將轉換為位能,故而在槽底的液面形成『駐波』。這個現象在『河水』的『流速』突然『由快變慢』時也可能發生,因而有人能在『河裡衝浪』,他正站在『駐波』之上!!
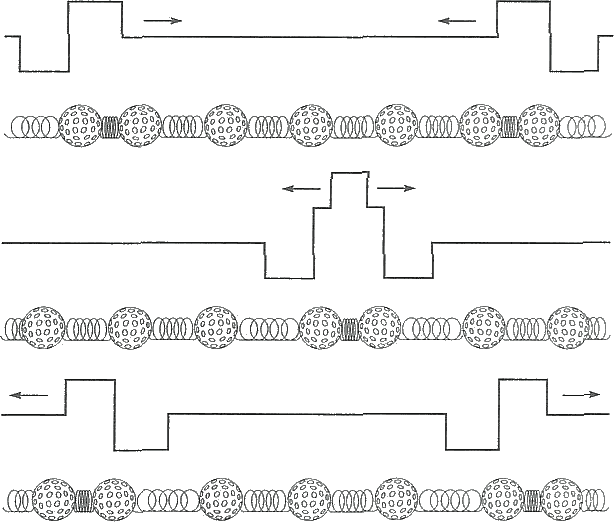
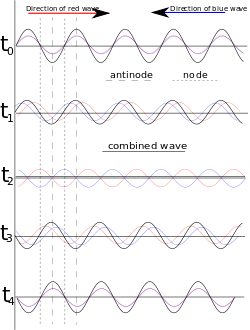
那什麼是『駐波』的呢?比方說一個『不動的』stationary 介質中,向左的波 ![]() 與向右的波
與向右的波 ![]() 疊加後的『合成波』
疊加後的『合成波』![]() ,在『特定』的『邊界條件』下,被『侷限』在一定『空間區域』內無法前進,因此稱為『駐波』。由於駐波不能傳播能量,它的能量將『儲存』在那個空間區域裡。駐波所在區域,『振幅為零』的點稱為『節點』或『波節』Node ,『振幅最大』的點位於兩『節點』之間,通常叫做『腹點』或『波腹』Antinode。
,在『特定』的『邊界條件』下,被『侷限』在一定『空間區域』內無法前進,因此稱為『駐波』。由於駐波不能傳播能量,它的能量將『儲存』在那個空間區域裡。駐波所在區域,『振幅為零』的點稱為『節點』或『波節』Node ,『振幅最大』的點位於兩『節點』之間,通常叫做『腹點』或『波腹』Antinode。
一根長度 ![]() 震盪的弦上,一個向右的簡諧波
震盪的弦上,一個向右的簡諧波 ![]() ,由於弦的兩頭固定,那個波在右端點也只能『反射』回來,形成了
,由於弦的兩頭固定,那個波在右端點也只能『反射』回來,形成了 ![]() ,此時合成波
,此時合成波 ![]() 是
是
![]()
,可用三角恆等式簡化為
![]()
。此時『時間項』與『空間項』分離,形成『駐波』。在 ![]() 時,
時,![]() ,此處
,此處 ![]() 是整數,這就是『節點』;當
是整數,這就是『節點』;當 ![]() 時
時 ![]() ,也就是『腹點』。當然波長
,也就是『腹點』。當然波長 ![]() 就得滿足
就得滿足 ![]() 的邊界條件。
的邊界條件。
─── 琴弦擇音而振, 苟非知音焉得共鳴。───