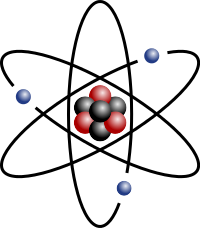
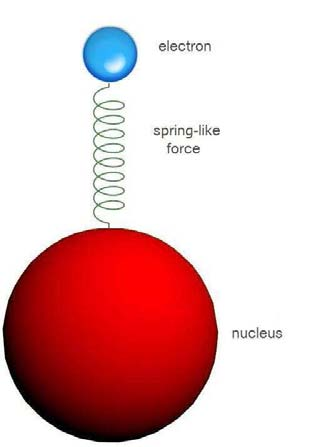
在量子力學被發現之前，一八七八年勞侖茲就利用『古典力學』與『電磁理論』，想像著『原子‧電磁場』會如何『交互作用』，並將此『模型』之表達為

，此處 是電子的『電荷』 庫倫， 是電子之『質量 公斤， 是電子所處的『時變電磁場』 。勞侖茲假設『原子核』與『電子』間的『束縛力』可以用『虎克定律』   來描述。並且假設『原子核』的質量遠大於『電子』的質量，因此可以看成只有『電子』在『假想原子核靜止』的『平衡位置』附近做『簡諧運動』，好比人們日常生活中活動在『靜止的大地』上。所以 就是這個『原子』振動的『自然頻率』。當年勞侖茲其實不能解釋『阻尼係數』 的真實成因；有了『量子力學』之後，人們才知道它有著來自於『原子碰撞』與『輻射量化』的種種原故。然而勞侖茲的確了解一加速帶電粒子會放射出『電磁輻射』，因此減少『動量』，現今稱之為『阿布拉罕‧勞侖茲力』Abraham-Lorentz force，數學上可以寫成

。假使計算一個『電子』輻射了『電磁波』，而這個『電磁波』又作用到那個電子『自己』，就引發了所謂的『自身場』self-fields 問題。在古典物理中， 它的數學求解會產生『未來的作用力影響了現在』的結果。事實上，自身場關係到『物質』與『能量』的『本質』，這個問題目前看來物理學家們也許尚在『爭論中』！！

那麼『勞侖茲振子模型』 Lorentz Oscillator Model 是否是一個『適切』的『物理模型』的呢？一般說來物理模型通常必須能夠『定量符合』觀察數據，並且『定性說明』物理現象。有時一個『良好』的物理模型還能『啟發』人們探究『新的』物理現象。在此就讓我們考察一下這個物理模型的定性之『合適性』和定量的『近似性』

一、氫原子 H 是質量最輕的原子，原子核只由一個『質子』 所構成，它的質量為 ，大約是『電子』的一千八百多倍。依據牛頓『作用反作用』第三運動定律，假使一個質量是 ，位置在    的『電子』與質量為   處之於 『原子核』  發生交互作用，運動方程式會滿足

，因此得到 ，所以 。如果選擇從『質心參考座標系』上來描述此兩者的運動，此時 ，得到 的關係式，也就是說

，因此可以講『靜止的原子核』與『在平衡位置附近做簡諧運動的電子』之假想是原子系統定性上說『合理的』的近似。

二、從數學上來說，我們可以用『泰勒級數』Taylor series 將一個『函數』 在任何『位置』展開。比方講假設於『平衡位置』 處附近觀察，可以得到

。如果說這個 就是『電子』與『原子核』之間的交互作用力，此式的前兩項 也就是『虎克定律』的『假設』了！真不知道到底有多少系統不可以用『虎克力』來作『近似處理』！！

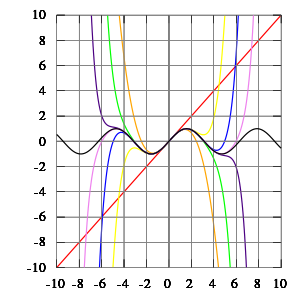
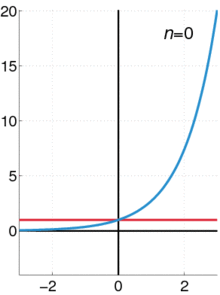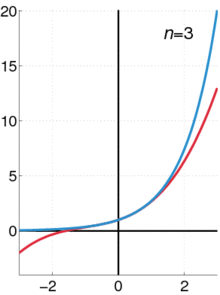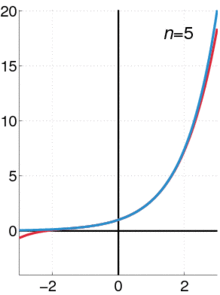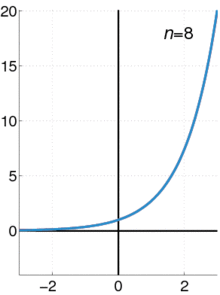
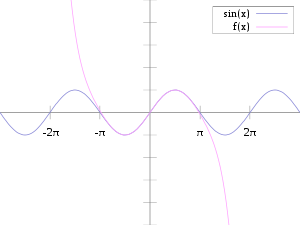
左圖中『粉紅色曲線』是『近似』 的七階泰勒多項式

，在 的區間裡，這個多項式近似的『誤差』小於 。因此，『原子核』與『電子』間的『束縛力』可以用『虎克定律』   來描述的『假設』，也是定量上講原子系統的『適切的』模型。