每日彙整: 2014-09-04

樹莓派、樹莓派之學習、樹莓派之教育

λ 運算︰計物數《遞迴補遺》

View of the restored paintings of the Ha

俄羅斯娃哇

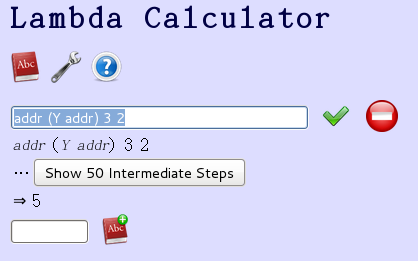
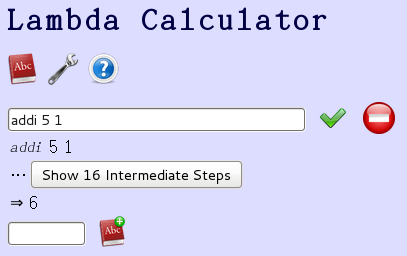
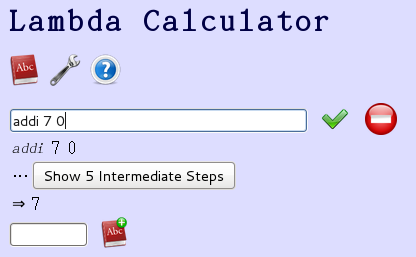
我喃喃自語說︰我做了一個夢。在那夢中我做了一個夢，我喃喃自語說︰我做了一個夢。宛如我置身『鏡廊』一面『鏡子』前，我見着了『鏡裡』的我置身『鏡廊』一面『鏡子』前，… \infty。

俄羅斯娃哇是『有趣的』事物，雖然只有『有限』的幾個『迭套』，它卻是『象徵』一個『不思議』的『奧秘』。其實『遞迴』Recursion 與『疊代』 Iteration 兩個概念，彼此間有著很深刻的『聯繫』。

為什麼數學上常常要用『遞迴定義』的呢？假使你出於『好玩』，想『定義』一個『數列』，那麼有什麼『簡單』的辦法的呢？

有人說︰這很簡單啊！就給一個 F_n 『公式』Formula 就好了，就好比講這個數列是

F_n =_{df} \Box \Box, n=0 \cdots \infty。

有人問︰萬一你不知道『那個公式』呢？還是說如果『公式不存在』這樣子就根本『沒辦法』去定義『數列』的呢？

有人答︰『可以』的啊！比方說假使你『知道』

一、F_0 的『值』

二、曉得如何從 F_k 『計算』出 F_{k+1} 的『值』，這樣就算是不知道 F_n 是能不能夠表達，一樣可以『定義』這個『數列』的啊！

據說義大利的數學家李奧納多‧費波那契 Leonardo Fibonacci 描述各代『兔子生育』總數目時得到這個數列︰

F_0 = 0
F_1 = 1
F_n = F_{n-1} + F_{n-2}

因此 F_2 = F_1 + F_0 = 1 + 0 = 1, F_3 = F_2 + F_1 = 1 + 1 = 2. \cdots，所以可以逐步的得到『費波那契數列』。當然可以求解那一個『差分方程式』得到

F_{n}=\frac{\sqrt{5}}{5} \cdot \left[\left(\frac{1 + \sqrt{5}}{2}\right)^{n} - \left(\frac{1 - \sqrt{5}}{2}\right)^{n}\right]。

然而並非所有可以『遞迴定義』的數列，都能有『公式解』，或者說還沒將它『算出來』。所以能這樣從幾個『初始資料』和一個『遞迴關係』來定義東西的方式，自然有它的好處的了。

一般人們用程式計算『數列』a_n 的『級數和』

S_n = a_0 + a_1+\cdots +a_n

，很自然的會用『疊代』的想法，可以表達為

R := a_0
R := R+ a_n, n=1 \cdots N

，此處『:=』表示變數『賦值』，逐項累加到所需要的 N 次。這或許是大部分的程式語言都有『FOR LOOP』的原因。但是遇到了像『河內塔』這一類問題，由於那個 a_n 本身就先需要計算出來，況且還和 a_k, k=1 \cdots n-1 有關，這時想寫個『疊代法』程式就很困難的了。所以『方法選擇』應當針對『問題狀況』，難有『萬能之法』的啊！

為了談談『疊代』與『遞迴』之間的『聯繫』，我們先舉一個如何用『遞迴』來寫『加法』例子︰

addr \ x, y =_{df}
IF y is 0 THEN x
ELSE addr (SUCC x) (PRED y)

將之翻譯成『Y組合子』用的『 λ表達式』︰

addr =_{df} \lambda f. \lambda x. \lambda y. IFTHENELSE \ (ISZERO \ y) \ (x) \ (f \ (SUCC \ x) \ (PRED \ y))

addr(Yaddr)-3-2

從這個翻譯來看，因為 λ表達式不能直接指涉『addr』之故，所以才需要這個『佔位置』變元 f，當化約『addr (Y \ addr) \ 3 \ 2』時，變元 f 就是表示『Y \ addr』 這個函式。

假使我們知道 y \leq 1，那麼可以『手動』改寫『addr』為︰

addi \ x, y =_{df}
IF y is 0 THEN x
ELSE (
IF ((PRED y) is 0) THEN (SUCC x)
ELSE (
IF (PRED (PRED y) is 0) THEN SUCC(SUCC x)
ELSE (0) ※FAIL
)

並且翻譯成 Lambda Calculator 寫法

\x.\y. IFTHENELSE (ISZERO y) (x) (IFTHENELSE (ISZERO (PRED y)) (SUCC x)  (IFTHENELSE (ISZERO (PRED (PRED y))) (SUCC (SUCC x) )  (0) ))

addi-5-1
addi 5 1

addi 7 0
addi-7-0

也就是說有限的遞迴通常可以手動的『複製遞迴計算』，自己賦與遞迴中所需要的『呼叫參數值』，改寫成『非遞迴』的『長版本程式』。這個程式中有許多的『自我相似』的『程式碼』，彷彿是個『俄羅斯娃娃』的『構造』一般！如果將它翻譯成『疊代』的程式，經常會作『概念改寫』︰將 y 減一，且將 x 加一，直到 y = 0 為止。它雖然經常能夠得到『短版本程式』，但是兩者間的『概念聯繫』是很明晰的啊！！

所以當我們還不清楚可能的『計算步驟』時『遞迴』有『優勢』，如果有對等的『疊代』程式通常『執行速度』會比較『快』，因此許多程式語言也有使用『中止條件』的『WHILE LOOP』之建構。萬一『中止條件』在有限時間裡始終達不到，或許將會陷入『無窮循環』，這時兩者狀況是相似的。但是也不要以為『無窮循環』就一定是『不好的』，有時候它正是所要的『目的』，就像『CPU』開機後就一直運作執行一樣。

為什麼 λ表達式無法『直接指涉』自身的呢？因為在『純  λ語言』裡你無法『定義』標示符號，所以當表達成

\Box =_{df} \cdots \Box \cdots

，這只是為了方便的說法，無法如設想的『化約』表達式中 \Box 是『定義』的『引用』，它在『化約』時只會被當成一個叫做 \Box 的『變元』，於是根本就達不成『遞迴』之目的了。