【越調】天淨沙‧秋思
元 馬致遠
枯籐老樹昏鴉,
小橋流水人家,
古道西風瘦馬。
夕陽西下,
斷腸人在天涯。
繪畫、照片與書法是哪種比較『寫實』?哪個又較為『抽象』?《秋思》中用具象《『藤』、『樹』、『鴉』》,來虛寫『時光變化』之《『枯』、『老』、『昏』》;以實景《『橋』、『水』、『家』》,將串成『應歸之所』的《『小』、『流』、『人』》;終至於『道』得『古』、『風』是『西』、『馬』又怎能不『廋』?此刻也許只該是『夕陽西下』??否則哪歸結的出『胡不歸去』之『斷腸人在天涯』!!
或許『失重』的『實物』漂浮於天之涯海之角,反而更顯得『虛幻』的了!!而『抽象』的『圖形』一旦擬似具體構物,或會因『沈重』終將失去『空靈』的嗎??
在《啃一塊唄 K TCPIP!!下》一文中,我們談到『TCP/IP』規範堆疊的『層層包裹』,目的是為了方便寫程式的人,無須理會太多『具體詳細』的『實作』,這能減少程式的『複雜度』,也使得它容易『分層除錯』。也就是說計算機科學中一般所謂的『抽象化』Abstraction 是一種『程序』與『資料』的『封裝』方式,使用該程序或資料的人透過封裝之『應用界面』的『用法說明』來調用,不必知道『那裡頭是怎麼作的』。這麼說來這個『抽象的目的』反倒是為了『實用性』的了!!
就讓我們進入邱奇數的『抽象世界』稍稍『領略』一下到底如何建構這個『抽象物』的系統的呢?首先我們列出幾個上一篇中定義的邱奇自然數︰
0 [\f.\x.x] = \f.\x.x
1 [SUCC 0] = \f.\x.f x
2 [SUCC 1] = \f.\x.f (f x)
3 [SUCC 2] = \f.\x.f (f (f x))
4 [SUCC 3] = \f.\x.f (f (f [f x]))
…
,它是一個有兩個輸入變元 ![]() 的函式,對於自然數
的函式,對於自然數 ![]() 的結構也許可以簡潔點的表達為
的結構也許可以簡潔點的表達為
![]()
,也就是說變元 ![]() 為變元函式
為變元函式 ![]() 應用
應用 ![]() 次。那麼
次。那麼
![]()
,就是『自然數 ![]() 之函式』針對變元
之函式』針對變元 ![]() 替換為
替換為 ![]() ,變元
,變元 ![]() 替換為
替換為 ![]() 的化約求值,這時它已經沒有輸入變元
的化約求值,這時它已經沒有輸入變元 ![]() 的了。這有什麼重要的嗎?由於我們只能夠使用函式『應用』來『解封』函式,比方說要怎麼樣才能得到
的了。這有什麼重要的嗎?由於我們只能夠使用函式『應用』來『解封』函式,比方說要怎麼樣才能得到 ![]() 中的『運算規則』
中的『運算規則』 ![]() 的呢?難道不能用
的呢?難道不能用 ![]() 的嗎?這就是『解讀』SUCC 定義的關鍵,它使用
的嗎?這就是『解讀』SUCC 定義的關鍵,它使用 ![]() 『解封』輸入的自然數變元
『解封』輸入的自然數變元 ![]() ,然後再用變元
,然後再用變元 ![]() 將多作一次
將多作一次 ![]() 的結果『封裝』起來成為自然數
的結果『封裝』起來成為自然數 ![]() ︰
︰
![]()
![]()
![]()
![]()
,因此 SUCC 之所以用 ![]() 的結構,它的目的是十分自然清楚,因為所謂的『後繼數』需要多一個
的結構,它的目的是十分自然清楚,因為所謂的『後繼數』需要多一個 ![]() 。
。
從數學的角度上來看,如果知道怎麼作『 ![]() 』,那麼所謂的『
』,那麼所謂的『 ![]() 』就是將『
』就是將『 ![]() 』作
』作 ![]() 次,於是
次,於是
![]()
![]()
![]()
![]()
![]()
![]()
就是它的程式設計『實作』。
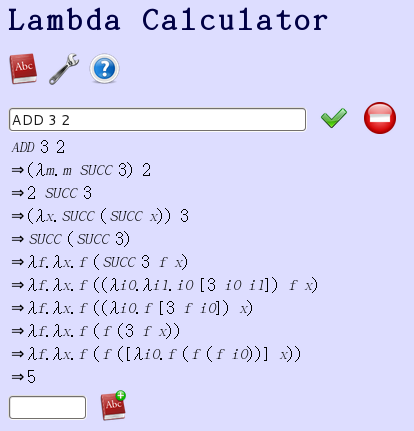
左上圖是『ADD 3 2』的化約過程,而上一篇中的『 + 』的定義
![]()
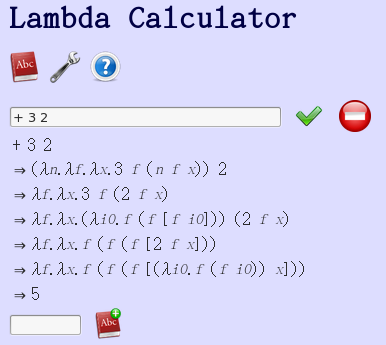
並不是『間接』使用『後繼數』作法,而是將該作法結構 ![]() 『直接』利用,可以看成是將加法程式作『最佳化』,左下圖是它的化約過程,讀者可以自行比較。
『直接』利用,可以看成是將加法程式作『最佳化』,左下圖是它的化約過程,讀者可以自行比較。
一個『演算法』當然最好能夠既『清晰』易解,又『執行』快速,然而當這兩方『不可兼得』的時候,也許需要考慮『硬體限制』與『應用目的』才能作『取捨』的吧!
再從數學的角度上來講,假使我們已經知道了兩個數的『加法』,那麼『乘法』![]() 就是將
就是將 ![]() 加上
加上 ![]() 作
作 ![]() 次。也就是說
次。也就是說 ![]() ,於是我們可以將『乘法』寫成︰
,於是我們可以將『乘法』寫成︰
![]()
![]()
![]()
![]()
![]()
左圖是『MULT 3 2』的 ![]() 化約過程。
化約過程。
由於邱奇自然數是一種稱之為『高階函式』Higher-order function 的構造,所以『算術加乘』的定義也就在泛函式的運作下來考量。數學上的『對等的表達式』是很有用的『實作』方向『指引』。或許『玩 λ 運算』未必會『喪志』,過程中的『樂趣』也許正在於『思考』之『苦惱』以及『表達』的『困難』。
佛經上有言︰煩惱即菩提!!
─── 待續… λ 運算︰計物數《下》───