每日彙整: 2016-06-13

樹莓派、樹莓派之學習、樹莓派之教育

W!o+ 的《小伶鼬工坊演義》︰神經網絡【隨機變數】二

假使說有人想借著維基百科詞條來學習『機率論』，大概不切實際吧？甚或不可思議耶！如果就人類歷史上原初

事件

單位事件、事件空間、隨機事件

在一次隨機試驗中可能發生的不能再細分的結果被稱為基本事件，或者稱為單位事件，用 E 表示。在隨機試驗中可能發生的所有單位事件的集合稱為事件空間，用 S 來表示。例如在一次擲骰子的隨機試驗中，如果用獲得的點數來表示單位事件，那麼一共可能出現 6 個單位事件，則事件空間可以表示為 S = { 1 , 2 , 3 , 4 , 5 , 6 } 。

上面的事件空間是由可數有限單位事件組成，事實上還存在著由可數無限以及不可數單位事件組成的事件空間，比如在一次獲得正面朝上就停止的隨機擲硬幣試驗中，其事件空間由可數無限單位事件組成，表示為： S = { 正，反正，反反正，反反反正，反反反反正， ···}，注意到在這個例子中”反反反正”是單位事件。將兩根筷子隨意扔向桌面，其靜止後所形成的交角假設為 α ，這個隨機試驗的事件空間的組成可以表示為 S = { α | 0 ∘ ≤ α < 180 ∘ } 。

隨機事件是事件空間 S 的子集，它由事件空間 S 中的單位元素構成 ，用大寫字母 A , B , C ⋯ 表示。例如在擲兩個骰子的隨機試驗中，設隨機事件 A = 「獲得的點數和大於10」，則 A 可以由下面 3 個單位事件組成： A = { ( 5 , 6 ) , ( 6 , 5 ) , ( 6 , 6 ) } 。

如果在隨機試驗中事件空間中的所有可能的單位事件都發生，這個事件被稱為 必然事件，表示為 S ⊂ S ；相應的如果事件空間裡不包含任何一個單位事件，則稱為不可能事件，表示為 ∅ ⊂ S 。

事件的計算

因為事件在一定程度上是以集合的含義定義的，因此可以把集合計算方法直接應用於事件的計算，也就是說，在計算過程中，可以把事件當作集合來對待。

Komplement3.png
A 的補集
不屬於 A 的事件發生		 Vereinigung.png
並集 A ∪ B
或者 A 或者 B 或者 A , B 同時發生		 Durchschnitt.png
交集 A ∩ B
事件 A , B 同時發生
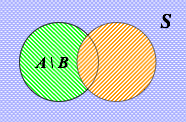Differenz.png
差集 A \ B
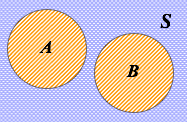不屬於 B 的 A 事件發生		 Disjunkte.png
空集 A ∩ B = ∅
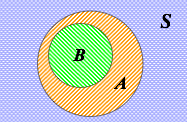A , B 事件不同時發生		 Impliziert.png
子集 B ⊆ A
如 B 發生，則 A 也一定發生

在輪盤遊戲中假設 A 代表事件「球落在紅色區域」， B 代表事件”球落在黑色區域”，因為事件 A 和 B 沒有共同的單位事件，因此可表示為

A ∩ B = ∅

注意到事件 A 和 B 並不是互補的關係，因為在整個事件空間 S 中還有一個單位事件「零」，其即不是紅色也不是黑色，而是綠色，因此 A , B 的補集應該分別表示如下：

A ¯ = S ∖ A = B ∪ { 0 }
B ¯ = S ∖ B = A ∪ { 0 }

───

 

立論，或許這人還比『帕斯卡』所站的位置好呢！！

歷史

作為數學統計基礎的機率論的創始人分別是法國數學家帕斯卡和費馬，其可追溯到公元17世紀。 當時的法國宮廷貴族裡盛行著擲骰子遊戲，遊戲規則是玩家連續擲4次骰子，如果其中沒有6點出現，玩家贏，如果出現一次6點，則莊家（相當於現在的賭場） 贏。按照這一遊戲規則，從長期來看，莊家扮演贏家的角色，而玩家大部分時間是輸家，因為莊家總是要靠此為生的，而當時人們也接受了這種現象。

後來為了使遊戲更刺激，遊戲規則發生了些許變化，玩家這回用2個骰子連續擲24次，不同時出現2個6點，玩家贏，否則莊家贏。當時人們普遍認為，2 次出現6點的機率是一次出現6點的機率的1 / 6，因此6倍於前一種規則的次數，也既是24次贏或輸的機率與以前是相等的。然而事實卻並非如此，從長期來看，這回莊家處於輸家的狀態，於是他們去請教當 時的數學家帕斯卡，求助其對這種現象作出解釋。

其他對機率論的發展作出重要貢獻的人還有荷蘭物理、數學家惠更斯，瑞士物理、數學家伯努利，法國數學家棣莫弗，法國數學、天文學家拉普拉斯，德國數學家高斯，法國物理、數學家泊松，義大利數學、醫學家卡爾達諾以及蘇聯數學家柯爾莫哥洛夫。

───

 

『機率論』發展至今，已經抽象濃縮成如斯矣︰

數學處理

主條目：機率公理

事件A的機率一般會寫成P(A)、p(A)或Pr(A)[8]。機率的數學概念可以延伸到無限的樣本空間甚至不可數的樣本空間，但需要用上機率測度的概念。

機率的公理化定義將機率的相關範疇從具體問題中抽象出來，從而可以在數學意義下考察機率的相關概念和由之引出的問題。以下給出機率的公理化定義：

設隨機事件的樣本空間為Ω，Ω的一個子集稱為事件。對於Ω中的每一個事件A，都有實函數P(A)，滿足：

  1. 非負性： P ( A ) ≥ 0 ；
  2. 規範性： P ( Ω ) = 1
  3. 可數可加性：對可數個兩兩互斥事件{Ai}i∈N有： \sum \limits_{i=1}^{\infty} P (A_i) = P (\cup \limits_{i=1}^{\infty} A_i)

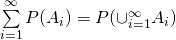
任意一個滿足上述條件的函數P都可以作為樣本空間Ω的機率函數，稱函數值P(A)為Ω中事件A的機率。

表示機率

一個事件的機率值通常以一個介於0到1的實數來表示。一個不可能事件其機率值為0，而確定事件其機率值則為1。 但反推並不成立，也就是說機率值為0的事件不表示它就是一個不可能事件，同理，機率值為1的事件不表示它就一定發生。例如，在一個正方形內作一條線段，由 於這條線段的面積是0，所以一個點落在這條線段上的機率就是0，但它並不是不可能事件。

實際上大多數的機率值都是介於0與1之間的數，這個數示代表事件在’不可能發生’與’確定發生’之間的相對位置。事件的機率值越接近1，事件發生的機會就越高。

舉例來說，假設兩個事件有相同的發生機率，就像被拋擲而落地的銅板不是正面向上就是反面向上一樣，但是我們不能說：每2次拋擲會出現1次，只能說事件發生的機率是平均每2次出現一次，或說是 “50%” 或 “1/2″。

分布

機率分布函數是一個把機率分配給事件或者命題的函數。對於任何一個事件或者命題，總有很多分配機率的方法，所以選擇不同的分布等同於對一個問題中的事件或者命題作出不同的假設。

分布還可分為「離散」和「連續」的。

機率計算總結

機率計算總結
事件 機率
A P ( A ) ∈ [ 0 , 1 ]
非A P ( A c ) = 1 − P ( A )
A或B P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A ∩ B ) P ( A ∪ B ) = P ( A ) + P ( B ) if A and B are mutually exclusive
A和B P ( A ∩ B ) = P ( A | B ) P ( B ) = P ( B | A ) P ( A ) P ( A ∩ B ) = P ( A ) P ( B ) if A and B are independent
B的情況下A的機率 P ( A ∣ B ) = P ( A ∩ B ) P ( B ) = P ( B | A ) P ( A ) P ( B )

───

 

為什麼『機率為零』的事件並非『不可能』事件的呢？？這是因為『機率賦值』所致。設想一『實數線段』，由於『實數』是不可數的無窮多。於是在此線段中任一有限個數所構成的集合，從『長度測度』的觀點下只能是個『零』！事實上即使用『取其半』的無窮之數來構成集合，其以長度為尺之『機率度量』依然是個『零』！ ！那麼又為什麼『機率為一』的事件不是『必然』事件的呢？？擲一個兩面都是『頭』的硬幣，『必然』得到的結果是個『頭』嗎？或許那個硬幣它可以『立起來』的耶！！

如是當知機率概念之深奧也。更別講何謂『統計獨立性』的哩︰

條件機率

條件機率（英語：conditional probability）就是事件A在另外一個事件B已經發生條件下的發生機率。條件機率表示為P（A|B），讀作「在B條件下A的機率」。

聯合機率表示兩個事件共同發生的機率。A與B的聯合機率表示為 P ( A ∩ B ) 或者 P ( A , B ) 。

邊緣機率是某個事件發生的機率。邊緣機率是這樣得到的：在聯合機率中，把最終結果中不需要的那些事件合併成其事件的全機率而消失（對離散隨機變量用求和得全機率，對連續隨機變量用積分得全機率）。這稱為邊緣化（marginalization）。A的邊緣機率表示為P（A），B的邊緣機率表示為P（B）。

需要注意的是，在這些定義中A與B之間不一定有因果或者時間順序關係。A可能會先於B發生，也可能相反，也可能二者同時發生。A可能會導致B的發生，也可能相反，也可能二者之間根本就沒有因果關係。

定義

在同一個樣本空間Ω中的事件或者子集A與B，如果隨機從Ω中選出的一個元素屬於B，那麼這個隨機選擇的元素還屬於A的機率就定義為在B的前提下A的條件機率。從這個定義中，我們可以得出

P(A|B) = |A∩B|/|B|

分子、分母都除以|Ω|得到

P(A|B) = \frac{P(A \cap B)}{P(B)}

有時候也稱為：後驗機率

統計獨立性

若且唯若兩個隨機事件A與B滿足

P ( A ∩ B )   =   P ( A ) P ( B )

的時候，它們才是統計獨立的，這樣聯合機率可以表示為各自機率的簡單乘積。

同樣，對於兩個獨立事件A與B有

P ( A | B )   =   P ( A )

以及

P ( B | A )   =   P ( B ) 。

換句話說，如果A與B是相互獨立的，那麼A在B這個前提下的條件機率就是A自身的機率；同樣，B在A的前提下的條件機率就是B自身的機率。

互斥性

若且唯若A與B滿足

P ( A ∩ B ) = 0

且

P ( A ) ≠ 0 ， P ( B ) ≠ 0

的時候，A與B是互斥的。

因此，

P ( A ∣ B ) = 0
P ( B ∣ A ) = 0 。

換句話說，如果B已經發生，由於A不能B在同一場合下發生，那麼A發生的機率為零；同樣，如果A已經發生，那麼B發生的機率為零。

───

 

此事 Mark Kac 教授曾寫

STATISTICAL INDEPENDENCE IN PROBABILITY, ANALYSIS AND NUMBER THEORY

Independence

 

專論探討。深具啟發性或值一讀的乎！！！