洋洋灑灑之文，自然成章，根本無可註解。但請跟著 Michael Nielsen 先生來趟發現之旅耶！！

The vanishing gradient problem

So, what goes wrong when we try to train a deep network?

To answer that question, let’s first revisit the case of a network with just a single hidden layer. As per usual, we’ll use the MNIST digit classification problem as our playground for learning and experimentation*

*I introduced the MNIST problem and data here and here..

If you wish, you can follow along by training networks on your computer. It is also, of course, fine to just read along. If you do wish to follow live, then you’ll need Python 2.7, Numpy, and a copy of the code, which you can get by cloning the relevant repository from the command line:

git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git

If you don’t use git then you can download the data and code here. You’ll need to change into the src subdirectory.

Then, from a Python shell we load the MNIST data:

>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()

We set up our network:

>>> import network2
>>> net = network2.Network([784, 30, 10])

This network has 784 neurons in the input layer, corresponding to the pixels in the input image. We use 30 hidden neurons, as well as 10 output neurons, corresponding to the 10 possible classifications for the MNIST digits (‘0’, ‘1’, ‘2’, , ‘9’).

Let’s try training our network for 30 complete epochs, using mini-batches of 10 training examples at a time, a learning rate , and regularization parameter . As we train we’ll monitor the classification accuracy on the validation_data*

*Note that the networks is likely to take some minutes to train, depending on the speed of your machine. So if you’re running the code you may wish to continue reading and return later, not wait for the code to finish executing.:

>>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, 
... evaluation_data=validation_data, monitor_evaluation_accuracy=True)

We get a classification accuracy of 96.48 percent (or thereabouts – it’ll vary a bit from run to run), comparable to our earlier results with a similar configuration.

Now, let’s add another hidden layer, also with 30 neurons in it, and try training with the same hyper-parameters:

>>> net = network2.Network([784, 30, 30, 10])
>>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, 
... evaluation_data=validation_data, monitor_evaluation_accuracy=True)

This gives an improved classification accuracy, 96.90 percent. That’s encouraging: a little more depth is helping. Let’s add another 30-neuron hidden layer:

>>> net = network2.Network([784, 30, 30, 30, 10])
>>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, 
... evaluation_data=validation_data, monitor_evaluation_accuracy=True)

That doesn’t help at all. In fact, the result drops back down to 96.57 percent, close to our original shallow network. And suppose we insert one further hidden layer:

>>> net = network2.Network([784, 30, 30, 30, 30, 10])
>>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, 
... evaluation_data=validation_data, monitor_evaluation_accuracy=True)

The classification accuracy drops again, to 96.53 percent. That’s probably not a statistically significant drop, but it’s not encouraging, either.

This behaviour seems strange. Intuitively, extra hidden layers ought to make the network able to learn more complex classification functions, and thus do a better job classifying. Certainly, things shouldn’t get worse, since the extra layers can, in the worst case, simply do nothing*

*See this later problem to understand how to build a hidden layer that does nothing.

. But that’s not what’s going on.

So what is going on? Let’s assume that the extra hidden layers really could help in principle, and the problem is that our learning algorithm isn’t finding the right weights and biases. We’d like to figure out what’s going wrong in our learning algorithm, and how to do better.

To get some insight into what’s going wrong, let’s visualize how the network learns. Below, I’ve plotted part of a [784,30,30,10] network, i.e., a network with two hidden layers, each containing 30 hidden neurons. Each neuron in the diagram has a little bar on it, representing how quickly that neuron is changing as the network learns. A big bar means the neuron’s weights and bias are changing rapidly, while a small bar means the weights and bias are changing slowly. More precisely, the bars denote the gradient for each neuron, i.e., the rate of change of the cost with respect to the neuron’s bias. Back in Chapter 2 we saw that this gradient quantity controlled not just how rapidly the bias changes during learning, but also how rapidly the weights input to the neuron change, too. Don’t worry if you don’t recall the details: the thing to keep in mind is simply that these bars show how quickly each neuron’s weights and bias are changing as the network learns.

To keep the diagram simple, I’ve shown just the top six neurons in the two hidden layers. I’ve omitted the input neurons, since they’ve got no weights or biases to learn. I’ve also omitted the output neurons, since we’re doing layer-wise comparisons, and it makes most sense to compare layers with the same number of neurons. The results are plotted at the very beginning of training, i.e., immediately after the network is initialized. Here they are*

*The data plotted is generated using the program generate_gradient.py. The same program is also used to generate the results quoted later in this section.:

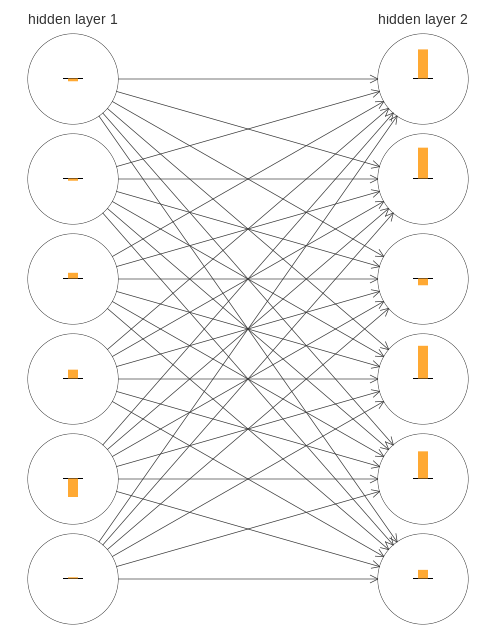
The network was initialized randomly, and so it’s not surprising that there’s a lot of variation in how rapidly the neurons learn. Still, one thing that jumps out is that the bars in the second hidden layer are mostly much larger than the bars in the first hidden layer. As a result, the neurons in the second hidden layer will learn quite a bit faster than the neurons in the first hidden layer. Is this merely a coincidence, or are the neurons in the second hidden layer likely to learn faster than neurons in the first hidden layer in general?

To determine whether this is the case, it helps to have a global way of comparing the speed of learning in the first and second hidden layers. To do this, let’s denote the gradient as , i.e., the gradient for the th neuron in the th layer*

*Back in Chapter 2 we referred to this as the error, but here we’ll adopt the informal term “gradient”. I say “informal” because of course this doesn’t explicitly include the partial derivatives of the cost with respect to the weights, .

. We can think of the gradient as a vector whose entries determine how quickly the first hidden layer learns, and as a vector whose entries determine how quickly the second hidden layer learns. We’ll then use the lengths of these vectors as (rough!) global measures of the speed at which the layers are learning. So, for instance, the length measures the speed at which the first hidden layer is learning, while the length measures the speed at which the second hidden layer is learning.

With these definitions, and in the same configuration as was plotted above, we find and . So this confirms our earlier suspicion: the neurons in the second hidden layer really are learning much faster than the neurons in the first hidden layer.

What happens if we add more hidden layers? If we have three hidden layers, in a [784,30,30,30,10] network, then the respective speeds of learning turn out to be 0.012, 0.060, and 0.283. Again, earlier hidden layers are learning much slower than later hidden layers. Suppose we add yet another layer with 30 hidden neurons. In that case, the respective speeds of learning are 0.003, 0.017, 0.070, and 0.285. The pattern holds: early layers learn slower than later layers.

We’ve been looking at the speed of learning at the start of training, that is, just after the networks are initialized. How does the speed of learning change as we train our networks? Let’s return to look at the network with just two hidden layers. The speed of learning changes as follows:

In any case, as you can see the two layers start out learning at very different speeds (as we already know). The speed in both layers then drops very quickly, before rebounding. But through it all, the first hidden layer learns much more slowly than the second hidden layer.

What about more complex networks? Here’s the results of a similar experiment, but this time with three hidden layers (a [784,30,30,30,10] network):

We have here an important observation: in at least some deep neural networks, the gradient tends to get smaller as we move backward through the hidden layers. This means that neurons in the earlier layers learn much more slowly than neurons in later layers. And while we’ve seen this in just a single network, there are fundamental reasons why this happens in many neural networks. The phenomenon is known as the vanishing gradient problem*

*See Gradient flow in recurrent nets: the difficulty of learning long-term dependencies, by Sepp Hochreiter, Yoshua Bengio, Paolo Frasconi, and Jürgen Schmidhuber (2001). This paper studied recurrent neural nets, but the essential phenomenon is the same as in the feedforward networks we are studying. See also Sepp Hochreiter’s earlier Diploma Thesis, Untersuchungen zu dynamischen neuronalen Netzen (1991, in German)..

Why does the vanishing gradient problem occur? Are there ways we can avoid it? And how should we deal with it in training deep neural networks? In fact, we’ll learn shortly that it’s not inevitable, although the alternative is not very attractive, either: sometimes the gradient gets much larger in earlier layers! This is the exploding gradient problem, and it’s not much better news than the vanishing gradient problem. More generally, it turns out that the gradient in deep neural networks is unstable, tending to either explode or vanish in earlier layers. This instability is a fundamental problem for gradient-based learning in deep neural networks. It’s something we need to understand, and, if possible, take steps to address.

One response to vanishing (or unstable) gradients is to wonder if they’re really such a problem. Momentarily stepping away from neural nets, imagine we were trying to numerically minimize a function of a single variable. Wouldn’t it be good news if the derivative was small? Wouldn’t that mean we were already near an extremum? In a similar way, might the small gradient in early layers of a deep network mean that we don’t need to do much adjustment of the weights and biases?

Of course, this isn’t the case. Recall that we randomly initialized the weight and biases in the network. It is extremely unlikely our initial weights and biases will do a good job at whatever it is we want our network to do. To be concrete, consider the first layer of weights in a [784,30,30,30,10] network for the MNIST problem. The random initialization means the first layer throws away most information about the input image. Even if later layers have been extensively trained, they will still find it extremely difficult to identify the input image, simply because they don’t have enough information. And so it can’t possibly be the case that not much learning needs to be done in the first layer. If we’re going to train deep networks, we need to figure out how to address the vanishing gradient problem.

───

此一『梯度消失問題』之提出

Vanishing gradient problem

In machine learning, the vanishing gradient problem is a difficulty found in training artificial neural networks with gradient-based learning methods and backpropagation. In such methods, each of the neural network’s weights receives an update proportional to the gradient of the error function with respect to the current weight in each iteration of training. Traditional activation functions such as the hyperbolic tangent function have gradients in the range (−1, 1) or [0, 1), and backpropagation computes gradients by the chain rule. This has the effect of multiplying n of these small numbers to compute gradients of the “front” layers in an n-layer network, meaning that the gradient (error signal) decreases exponentially with n and the front layers train very slowly.

With the advent of the back-propagation algorithm in the 1970s, many researchers tried to train supervised deep artificial neural networks from scratch, initially with little success. Sepp Hochreiter‘s diploma thesis of 1991^[1][2] formally identified the reason for this failure in the “vanishing gradient problem”, which not only affects many-layered feedforward networks, but also recurrent neural networks. The latter are trained by unfolding them into very deep feedforward networks, where a new layer is created for each time step of an input sequence processed by the network.

When activation functions are used whose derivatives can take on larger values, one risks encountering the related exploding gradient problem.

───

石破天驚，其人或將永垂神經網絡史乎？？

此一『扣鐘之問』，當真是大扣大鳴也！！？？

有時候『問』一個『好問題』，勝過『讀』萬卷『答案書』。就讓我們從了解什麼是『好問題』開始吧︰

已故的英國哲學家菲利帕‧福特 Philippa Foot，她於一九六七年發表了一篇名為《堕胎問题和教條雙重影響》論文，當中提出了『電車問題』，用來『批判』時下倫理哲學中之主流思想，尤其是功利主義的觀點︰

大部分之道德判斷都是依據『為最多的人謀取最大之利益』的『原则』而決定的。

她的原文引用如下︰

這個倫理學之『難題』現今有許多不同的類似之『版本』，也許是因為它是這個領域中最為知名的『思想實驗』之一的罷！！

─── 摘自《勇闖新世界︰ 《 pyDatalog 》 導引《十》豆鵝狐人之問題篇》