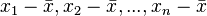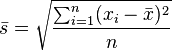假使思考使用『標準一公尺』之原器
公尺,中國大陸和香港音譯為米(亦稱公尺),台灣作公尺,口語有時也稱米。(英式英文:metre、美式英文:meter),是國際單位制基本長度單位,符號為m。[1]1公尺的長度最初定義為通過巴黎的經線上從地球赤道到北極點的距離的千萬分之一。其後隨著人們對度量衡學的認識加深,公尺的長度的定義幾經修改。從 1983 年至今,公尺的長度已經被定義為「光在真空中於 1/299792458 秒內行進的距離」。[2]
1889 年國際度量衡局改良第一代米原器的設計,所製作了的 X 形鉑銥合金棒,在 1889 年至1960 年間都是公尺的標準。
來度量一八七四年所製作的『米原器』。
即使在恆定的環境條件下,不同的『觀察者』之『讀取值』也可能不同。這或許真是『系統誤差』所講的
『個人誤差』又稱人員誤差,是由於測定人員的分辨力、反應速度的差異和固有習慣引起的誤差。這類誤差往往因人而異,因而可以採取讓不同人員進行分析,以平均值報告分析結果的方法予以限制 。
那麼要問的是這些相異的『量測值』是否會構成某種『機率分佈』Probability distribution ?如果用『數位顯示的』雷射測距儀能不能解決這個問題??由於那不自覺的『向左看』或『向右瞧』,因此發生『讀取值』的差異,卻很難『先驗』的說︰各向各種『偏差度 』機率相等。就像一人以『盡可能相同的方式』擲一粒『公正骰子 』,點數的分布會不會不同於『各面平均機會 ![]() 』的呢?也可以講『操作』雷射測距儀的『量測條件』的不確定性,恐將會打破那個『一致性』美夢的耶!!因是要從『真值』的觀點來看,不禁得問那個所謂的『平均值』一定會更『精準』的嗎??
』的呢?也可以講『操作』雷射測距儀的『量測條件』的不確定性,恐將會打破那個『一致性』美夢的耶!!因是要從『真值』的觀點來看,不禁得問那個所謂的『平均值』一定會更『精準』的嗎??
『多多益善』終究是個『假設』,一般或許常『習而不察』!人們若是不知現象的『機率分佈』,
Probability distribution
In probability and statistics, a probability distribution assigns a probability to each measurable subset of the possible outcomes of a random experiment, survey, or procedure of statistical inference. Examples are found in experiments whose sample space is non-numerical, where the distribution would be a categorical distribution; experiments whose sample space is encoded by discrete random variables, where the distribution can be specified by a probability mass function; and experiments with sample spaces encoded by continuous random variables, where the distribution can be specified by a probability density function. More complex experiments, such as those involving stochastic processes defined in continuous time, may demand the use of more general probability measures.
In applied probability, a probability distribution can be specified in a number of different ways, often chosen for mathematical convenience:
- by supplying a valid probability mass function or probability density function
- by supplying a valid cumulative distribution function or survival function
- by supplying a valid hazard function
- by supplying a valid characteristic function
- by supplying a rule for constructing a new random variable from other random variables whose joint probability distribution is known.
A probability distribution can either be univariate or multivariate. A univariate distribution gives the probabilities of a single random variable taking on various alternative values; a multivariate distribution (a joint probability distribution) gives the probabilities of a random vector—a set of two or more random variables—taking on various combinations of values. Important and commonly encountered univariate probability distributions include the binomial distribution, the hypergeometric distribution, and the normal distribution. The multivariate normal distribution is a commonly encountered multivariate distribution.
───
這個系統有沒有『內在機理』,縱使訴諸『大多數』,就『統計』推論而言,也只能是『邏輯誤謬』的吧!!
或許仔細閱讀並且深入了解一個良好『模型』,
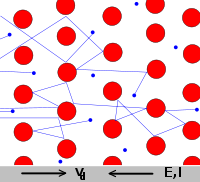
德國物理學家保羅‧卡爾‧路德維希‧德汝德 Paul Karl Ludwig Drude 於一九零零年提出了一個『電傳導』的模型。他想從『微觀』的角度來推導『歐姆定律』。雖然在今天或許需要一些量子力學的修正,這個古典簡單的模型卻提供了『金屬』中『直流電』和『交流電』的傳導、磁場的『霍爾效應』,以及『熱傳導』種種現象非常好的解釋。
德汝德將『導體』想像成由相對固定的『正離子』與可移動的『自由電子』所構成。這些為數眾多的『自由電子』彼此間不斷的發生『碰撞』,又和固定的『正離子』間也發生碰撞,彷彿就像在『彈珠台』裡的那些『彈珠』一樣。那麼到底這些『自由電子』的數量有多大的呢?如果用 ![]() 代表『電子密度』,
代表『電子密度』,![]() ,此處
,此處 ![]() 是阿佛加德羅常數,
是阿佛加德羅常數,![]() 是一個金屬原子貢獻多少個『自由電子』,
是一個金屬原子貢獻多少個『自由電子』,![]() 是金屬質量密度,
是金屬質量密度,![]() 是金屬的原子量。
是金屬的原子量。
舉例來說『鈉』 ![]() 很容易形成一價的『鈉離子』, 就說它的
很容易形成一價的『鈉離子』, 就說它的 ![]() ,如此
,如此 ![]() ,這樣一克的鈉,體積大約一立方公分,就有『數量級』為
,這樣一克的鈉,體積大約一立方公分,就有『數量級』為 ![]() 個『自由電子』。
個『自由電子』。
假使將它看成『自由電子氣體』,再利用奧地利物理學家路德維希‧愛德華‧波茲曼 Ludwig Eduard Boltzmann 所發展的古典氣體『運動理論』Kinetic theory 來探討這些『自由電子』,就如同理想氣體一樣,在『熱平衡』時,一個『自由電子』的『熱速度』 ![]() 可以用
可以用 ![]() 來計算,此處
來計算,此處 ![]() 是波茲曼常數
是波茲曼常數 ![]() ,
, ![]() 是『絕對溫標』。那麼室溫下
是『絕對溫標』。那麼室溫下 ![]() 的一個『自由電子』的『熱速度』大約是
的一個『自由電子』的『熱速度』大約是 ![]() 。
。
這個速度一秒大於百公里,不可謂之不大,假使用『費米氣體』的量子統計力學來講,更要大上個十倍,不過由於它在『各方向』的『均等性』,因此統計上來說『淨電流』的貢獻為『零』。也就是說 ![]() 。
。
那麼德汝德是如何看待這些『碰撞』作用的呢?或者說他做了哪些『假設』的呢?這點正是探討一個『物理模型』的『合理性』與『適切性』的重要之處。依據現今的說法,德汝德假設了︰
一、如果沒有外部的『電磁場』作用,『自由電子』將會作『直線運動』,彼此間的『電磁作用力』可以被忽略。這意味著是一種『獨立電子』的假設,它處於一個由『正離子』與『其他電子』所構成的『平均的環境』 ── 因此淨作用為零 ──,統計上來講這一般認為是『合宜的』。
二、『電子』和『正離子』之間的『碰撞』是『即時』的,統計上無關之『隨機事件』,所以總體來說這沒有任何『淨貢獻』,雖然有不同的學者『批評』它的『合宜性』。然而如果從『散射事件』來看,這也許只是說某些『物質屬性』之『均向性』的另一種說法罷了。
三、假設了『平均碰撞時間』 ![]() 的『存在』,所以我們可以說很小的一段時距
的『存在』,所以我們可以說很小的一段時距 ![]() 發生『碰撞』的『機會』是
發生『碰撞』的『機會』是 ![]() ,而且這個『機率』和一個『自由電子』的『位置』與『動量』無關。這正像是『丟一根』長度為
,而且這個『機率』和一個『自由電子』的『位置』與『動量』無關。這正像是『丟一根』長度為 ![]() 的『針』投到一個以
的『針』投到一個以 ![]() 為『格子線』板子上,問『針』掉到『線上』的『機率』大小如何,通常被認為是很好的『近似』。
為『格子線』板子上,問『針』掉到『線上』的『機率』大小如何,通常被認為是很好的『近似』。
四、『碰撞』後的『熱電子』應該保有該處『熱平衡』的速度。這是一個作用『鄰近原則』的假設,一般從『物理因果』上講,以為應是『正確的』。
─── 引自《【Sonic π】電聲學補充《三》上》
才是善法的耶!!
於此特將『德汝德模型』有關篇章索引如下,方便讀者之閱覽︰






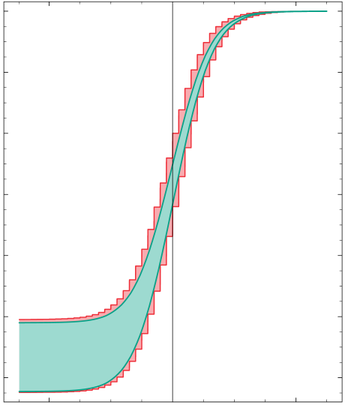
![[a, b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) and
and 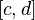 that are subsets of the real line
that are subsets of the real line  ,
,
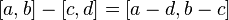


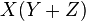 is a subset of
is a subset of  .
. we work with the two ends of the interval
we work with the two ends of the interval  and
and  , or could be one of them. Similarly a function
, or could be one of them. Similarly a function  when applied to
when applied to  for all
for all ![x \in [a,b]](https://upload.wikimedia.org/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) .
.
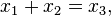
![[x_3]:=[x_3] \cap ([x_1]+[x_2])](https://upload.wikimedia.org/math/5/a/1/5a191d46fc2d6468d84abb172eb5eb54.png)
![[x_1]:=[x_1] \cap ( [x_3]-[x_2])](https://upload.wikimedia.org/math/8/c/3/8c3dd428e64f710a12bef35414d25c19.png)
![[x_2]:=[x_2] \cap ( [x_3]-[x_1])](https://upload.wikimedia.org/math/b/2/d/b2d8d5271be5a292e6e9d77215500a7e.png)
![x_1 \in [-\infty ,5],](https://upload.wikimedia.org/math/8/1/d/81d9446d44fa5f32b76f8198feee5152.png)
![x_2 \in [-\infty ,4],](https://upload.wikimedia.org/math/d/3/d/d3da81d29c6094261c40a2d3bdbe1472.png)
![x_3 \in [ 6,\infty]](https://upload.wikimedia.org/math/a/0/9/a094ca078f3c2199dca31c098cc45bb6.png)
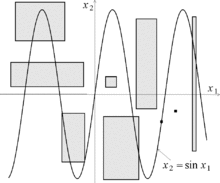
![x_3=x_1+x_2 \Rightarrow x_3 \in [6,\infty ] \cap ([-\infty,5]+[-\infty ,4]) =[6,\infty ] \cap [-\infty ,9]=[6,9].](https://upload.wikimedia.org/math/0/2/9/029b9a3771a955191e6bac82818b7dbb.png)
![x_1=x_3-x_2 \Rightarrow x_1 \in [-\infty ,5]\cap ([6,\infty]-[-\infty ,4]) =[-\infty ,5] \cap [2,\infty ]=[2,5].](https://upload.wikimedia.org/math/c/e/d/ced65ee1a92cd97e1d7f41e672302092.png)
![x_2=x_3-x_1 \Rightarrow x_2 \in [-\infty ,4]\cap ([6,\infty]-[-\infty ,5]) = [-\infty ,4] \cap [1,\infty ]=[1,4].](https://upload.wikimedia.org/math/b/7/d/b7dfc97fa1c6abeb20ed32dee3f40d39.png)

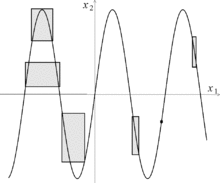


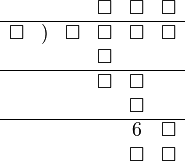
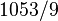 的直式
的直式 是
是 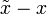 | 的前 m 個十進位數位為 0 ,隨後一位數字取值從 0 到 5 . 例如:
| 的前 m 個十進位數位為 0 ,隨後一位數字取值從 0 到 5 . 例如: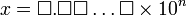 , 則
, 則 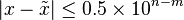 。
。









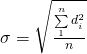 。
。

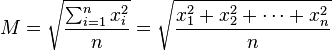
 的區間
的區間![\begin{smallmatrix}[a,b]\end{smallmatrix}](https://upload.wikimedia.org/math/0/2/c/02c2d84980612324d0b93ba4caebe459.png) 內,其均方根定義為:
內,其均方根定義為:![f_{\mathrm{rms}} = \sqrt {{1 \over {b-a}} {\int_{a}^{b} {[f(x)]}^2\, dx}}](https://upload.wikimedia.org/math/6/a/f/6af8508ff0c5072f3fb6695b669b0ab8.png)
 。
。 ,就是所有數據
,就是所有數據  和平均值
和平均值 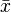 相減後的數據
相減後的數據