事物可『相連』未必能有『關係』的乎？俗話說︰事不關己，關心則亂！此事與矩陣光學何干耶？？也許下面文字可說明一二吧！！
或許有讀者會問『哲學』與『 pyDatalog 物件導向設計』有關嗎？值得花時間討論這種問題嘛！其實西方『理性主義』中之思辨精神也就是一種『□□方法學』。然而『方法學』不只一種，『思潮』也不只有一次，如是可以了解，下面這篇文章的『題旨』︰
或將知道『理念本身並不講話』，不同『詮釋』下也許『內容』可大不同。在面對『雲端大數據』新潮流時，勇闖新世界之先，能多作點準備罷了。假使真可以『比較哲學』，也許讀一段莊子，大概就能體會東方思辨以『生生取向』之大不同的吧︰
《莊子》‧《大宗師》
死 生，命也，其有夜旦之常，天也。人之有所不得與，皆物之情也 。彼特以天為父，而身猶愛之，而況其卓乎！人特以有君為愈乎己 ，而身猶死之，而況其真乎！泉涸，魚相與處於陸，相呴以溼，相濡以沫，不如相忘於江湖。與其譽堯而非桀，不如兩忘而化其道。夫大塊載我以形，勞我以生，佚 我以老，息我以死。故善吾生者，乃所以善吾死也。夫藏舟於壑，藏山於澤，謂之固矣。然而夜半有力者負之而走，昧者不知也。藏大小有宜，猶有所遯。若夫藏天 下於天下，而不得所遯，是恆物之大情也。特犯人之形而猶喜之，若人之形者，萬化而未始有極也，其為樂可勝計邪！故聖人將遊於物之所不得遯而皆存。善妖善 老，善始善終，人猶效之，又況萬物之所係，而一化之所待乎！
夫 道，有情有信，無為無形；可傳而不可受，可得而不可見；自本自根，未有天地，自古以固存；神鬼神帝，生天生地；在太極之先而不為高，在六極之下而不為深； 先天地生而不為久，長於上古而不為老。豨韋氏得之，以挈天地；伏犧氏得之，以襲氣母；維斗得之，終古不忒；日月得之，終古不息；堪坏得之，以襲崑崙；馮夷 得之，以遊大川；肩吾得之，以處太山；黃帝得之，以登雲天；顓頊得之，以處玄宮；禺強得之，立乎北極；西王母得之，坐乎少廣 ，莫知其始，莫知其終；彭祖得之，上及有虞，下及五伯；傅說得之，以相武丁，奄有天下，乘東維，騎箕尾，而比於列星。
── 摘自《勇闖新世界︰ 《 pyDatalog 》【專題】之物件導向設計 ‧三》
上篇『等效薄透鏡』說法，實則美矣！不過並未提及『節點』 nodal point 與『節面』 nodal plane 在哪哩？事實上它和『主平面』以及『主點』重合，可以驗以通過『節點』【※主點】之任意光 
，離開角度 
不變而得知︰
。
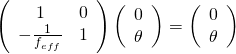如是對一個『厚透鏡』來說
，此處
， 
， 
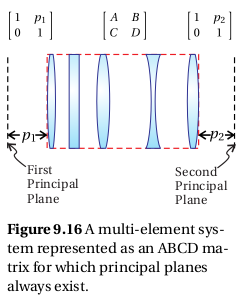
，這些點、面落在
位置。
比較與『頂點』 vertex 度量對應之『前焦距』為 
，『後焦距』是 
的了。因此 
就是 
的矣！ ！然而實務上即使知道了一光學系統之『前焦距』與『後焦距』，由於尚有 
、 
、 三個參數，且無法決定 的 呦？？
但思『焦、焦』面『參考系』︰
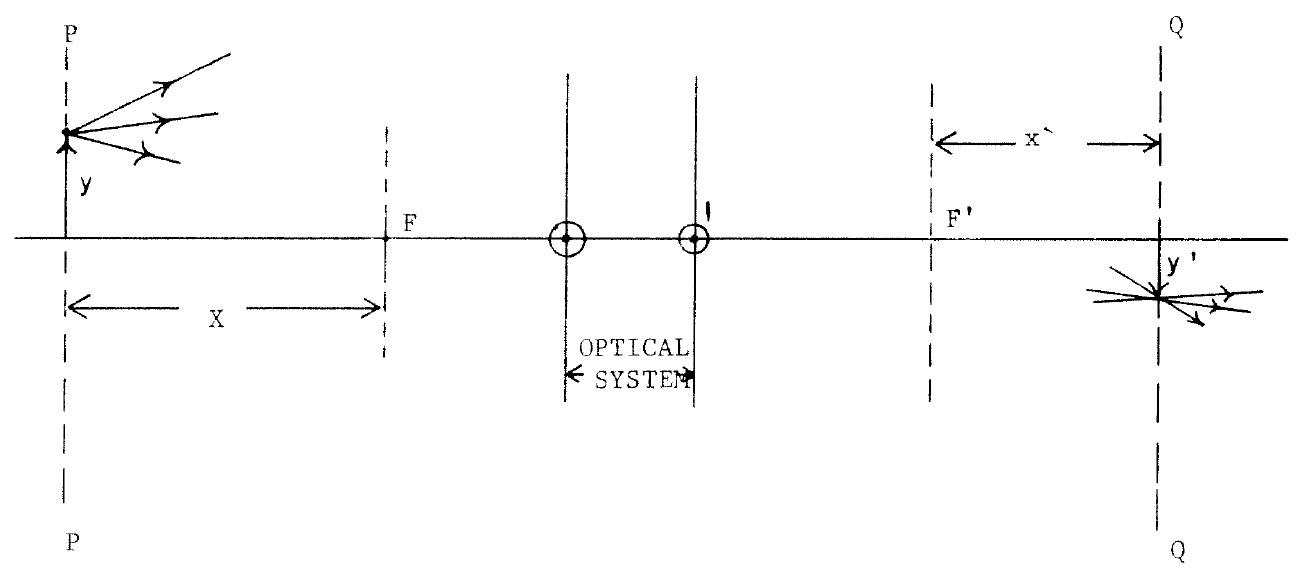
可用牛頓成像公式︰
。
假使考察『薄透鏡』之『焦、焦』面矩陣形制︰
成像條件可以推導為︰
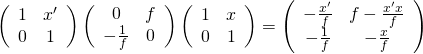
那麼當 
時，放大率等於
，如此當可確定 的吧 ！！？？
不知『厚透鏡』的『焦、焦』面矩陣形制是否也如此的呢？？？
pi@raspberrypi:~f \cdot (1 - \alpha) \cdot (1 + \gamma) + \beta = f
\frac{1}{f}
\frac{1}{f} = \frac{\alpha \gamma + \alpha - \gamma}{\beta}
f \cdot (1 - \alpha) \cdot (1 + \gamma) + \beta= f \cdot \left[ (1 - \alpha) \cdot (1 + \gamma) + \frac{\beta}{f} \right]= f \cdot \left[ (1 - \alpha) \cdot (1 + \gamma) + \alpha \gamma + \alpha - \gamma \right]= f \cdot 1$
誠神奇焉！！！
反想從『焦、焦』面倒推『主平面』與『主點』位置，終究是一樣的吧☆