24 | 8 月 | 2016 | FreeSandal

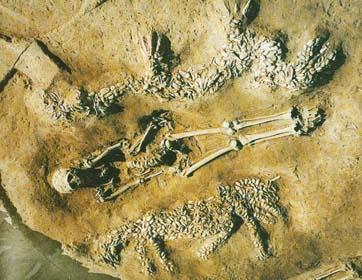
新石器時代仰韶文化中期，一個六千五百年前『濮陽西水坡』的墓穴，裡頭有一幅用『蚌殼』堆出的『龍虎圖』，刻意擺放的骸骨方位，到底在說著些什麼呢？中國的天文考古學家馮時先生認為︰

文本引自鄭杭生與胡翼鵬先生所寫的論文《天道左旋，天圆地方：社會運行的溯源和依據》
…
對這組蚌殼龍虎圖案解說最深入的研究者是天文考古學家馮時。馮時認為，解釋這幅蚌塑龍虎圖案的關鍵是墓主人脚下、正北面的那個蚌塑梯形與人體脛骨组成的圖案：這是一個北斗的造型，蚌塑梯形表示斗魁，東側横置的兩根脛骨表示斗杓，所以這是一個構造十分完整的二象北斗天象圖。

蚌塑梯形與脛骨構成的北斗圖象，不儘是從形狀上認證，更主要的是從表示斗杓的兩根人體脛骨去尋找線索。古代計算時間的一種方法，是通過對人體影子長短變化的測量，所以最初的測影工具是模仿人體来設計的，這就是“表”。正是因為人體、表與時間具有這種特殊關係，所以古人把計量時間的表叫作“髀”，而“髀”的本義是人體的腿骨，從大量的史料文獻中可以找到證據，古代測量日影的工具“表”就是由人骨轉變而來，所以人骨在作為一個生物體的同時，在古代還曾充當過測定日影的工具。濮陽西水坡４５號墓中的北斗圖，把腿骨、表和時間這三個方面聯繫起来，體現了古人通過立表測影和觀測北斗來測定時間這兩種方法的結合。在這個蚌殼梯形與脛骨的構圖中，脛骨的意義就是表示測定時間的工具。而北斗星也是古代中國人觀望天象，以此作為决定時間的標準星象。所以以脛骨作為這個構圖的長柄，結合整個構圖，可以認定蚌殼梯形與脛骨構成的圖案就是北斗星。確定了北斗星，再聯繫整個圖象的布局和造型，那麼這副蚌殼擺塑的龍和虎就只能作為星象來解釋，這樣本來孤立的龍虎圖由于北斗的存在而被自然地聯繫成了整體，成為天上的星宿和星象，即四象中的蒼龍和白虎。而那個制式奇特的墓穴，其形狀實際呈現了最原始的蓋天圖式，下半部的方形是大地，上半部的圓形是天穹，實則蕴藏著最原始的“天圓地方”觀念。

這個只有蚌殼作為随葬物品的墓穴中，竟然隱藏著“天”的秘密，陪葬墓主人的居然是整個天上的星斗。而那個北斗星的斗魁用貝殼，表明斗魁在天、在上；斗柄用人的腿骨，表明斗柄指地、在下。在天、在上，為神、為鬼；在地、在下，為巫、為人。它實際反映著古人頂天立地的幻想，所體現的是蒼天與大地的配合或聯繫，是神、鬼、人的相互交往。而且 6500 年前的古人對天象有如此精細的認識，說明他們的生活時時刻刻離不開對天象的觀察，不僅僅是觀象授時的實用層面上的應用，而如此虔誠的模擬，更說明他們的思想觀念和行為活動都受著“天”的無形制約。
…

在《馬太福音 25:29；》一文中，我們談到了『北極星』的不動與『太陽』之視運動，遠古之人就從觀察實踐中得出了『天圓地方』的『理念』，以及『天左旋，地右動』的『道理』。人們因著『觀測』天地事物，而能建立『理論』；追究『概念』的『緣由』以及『理則』之『依據』，所以創發『哲學』。因此在生活學習的道路上，其實是『事無古今，理無中外』，彼此『同異之間』的『匯通處』往往就是『基元』的『觀念』；『基元觀念』的不同『詮釋』成為相異的『學說體系』。事實上『字串改寫系統』、『圖靈機』與『 λ 運算』，說著『□□』的不同『側寫』，彼此之間可以用『○○』來對應『轉譯』，人們或說『同』或講『異』的各種『詮釋』就祇在其人的了！！

假使說給定了一個『 λ表達式』 $(\lambda x. ((\lambda y. (x \ y)) \ \Box) \ \bigcirc)$ ，有人『第一步』這樣作『 $\beta$ 化約』︰

$((\lambda y. ( \bigcirc \ y)) \ \Box )$

，也有人『第一步』這樣作『 $\beta$ 化約』︰

$(\lambda x. ( (x \ \Box ) \ \bigcirc)$

，這樣不同的『步驟選擇』是否會產生『不同結果』的呢？如果說再次繼續進行『 $\beta$ 化約』，兩者都會得到︰

$(\bigcirc \ \Box )$

，於是我們就可以歸結的說『 $\beta$ 化約』不管是用著怎麽樣的『步驟次序』，都一定能夠得到『相同結果』的嗎？？

─── 摘自《λ 運算︰概念導引《四》》

這裡引用『λ 運算』文本作起頭，祇是希望讀者能夠讀一讀，體會『符號』、『概念』、『表達』、『詮釋』、… 有著深刻的蘊函？常常看似南轅北轍的論事說理，往往發現其實內在機理互通！終究講述相同之事？？！！

現象既因相距 $L$ 之兩透鏡之組合而起︰

物 → 光 …… → 透鏡 $f_1$ → 距離 $L$ → 透鏡 $f_2$ …… → 像

且先列出其『光學矩陣』表達式︰

$\left( \begin{array}{cc} 1 & 0 \\ - \frac{1}{f_2} & 1 \end{array} \right) \left( \begin{array}{cc} 1 & L \\ 0 & 1 \end{array} \right) \left( \begin{array}{cc} 1 & 0 \\ - \frac{1}{f_1} & 1 \end{array} \right) = \left( \begin{array}{cc} 1 - \frac{L}{f_1} & L \\ \frac{L - (f_1 + f_2)}{f_1 \cdot f_2} & 1 - \frac{L}{f_2} \end{array} \right)$

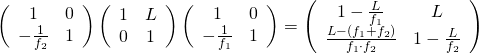
已知若其『等效』於『薄透鏡』，焦距 $- \frac{1}{f}$ 等於 $\frac{L - (f_1 + f_2)}{f_1 \cdot f_2}$ 。所以曉

‧ $L = 0$ 時， $\frac{1}{f} = \frac{1}{f_1} + \frac{1}{f_2}$ 。

‧ $L < f_1 + f_2$ 或 $L > f_1 + f_2$ 時，組合焦距可由該式算出。

因是問題就落在 $L = f_1 + f_2$ 的時候了。但思此刻之前、之後恰是 $L - (f_1 + f_2)$ 變號之際，也是組合透鏡或聚、或散性質變化之處，故而特殊的耶！！？？

何不就求得其表現

pi@raspberrypi:~  \left( \begin{array}{cc}
- \frac{f_2}{f_1} & f_1 + f_2 \\
0 & - \frac{f_1}{f_2} \end{array} \right) (h, \theta)h\thetaf \left( \begin{array}{cc}
1 & 0 \\
- \frac{1}{f} & 1 \end{array} \right) \theta = 0 fzh ipython3
Python 3.4.2 (default, Oct 19 2014, 13:31:11) 
Type "copyright", "credits" or "license" for more information.

IPython 2.3.0 -- An enhanced Interactive Python.
?         -> Introduction and overview of IPython's features.
%quickref -> Quick reference.
help      -> Python's own help system.
object?   -> Details about 'object', use 'object??' for extra details.

In [1]: from sympy import *

In [2]: from sympy.physics.optics import FreeSpace, FlatRefraction, ThinLens, GeometricRay, CurvedRefraction, RayTransferMatrix

In [3]: init_printing()

In [4]: f1, L, f2 = symbols('f1, L, f2')

In [5]: 相距L之兩薄透鏡組合 = ThinLens(f2) * FreeSpace(L) * ThinLens(f1)

In [6]: 相距L之兩薄透鏡組合
Out[6]: 
⎡     L                   ⎤
⎢   - ── + 1         L    ⎥
⎢     f₁                  ⎥
⎢                         ⎥
⎢         L               ⎥
⎢       - ── + 1          ⎥
⎢  1      f₂        L     ⎥
⎢- ── - ────────  - ── + 1⎥
⎣  f₂      f₁       f₂    ⎦

In [7]: 相距L之兩薄透鏡組合 = 相距L之兩薄透鏡組合.subs(L, f1 + f2)

In [8]: 相距L之兩薄透鏡組合
Out[8]: 
⎡       f₁ + f₂                 ⎤
⎢   1 - ───────        f₁ + f₂  ⎥
⎢          f₁                   ⎥
⎢                               ⎥
⎢           f₁ + f₂             ⎥
⎢       1 - ───────             ⎥
⎢  1           f₂        f₁ + f₂⎥
⎢- ── - ───────────  1 - ───────⎥
⎣  f₂        f₁             f₂  ⎦

In [9]: 相距L之兩薄透鏡組合 = RayTransferMatrix(相距L之兩薄透鏡組合.A.simplify(), 相距L之兩薄透鏡組合.B.simplify(), 相距L之兩薄透鏡組合.C.simplify(), 相距L之兩 薄透鏡組合.D.simplify())

In [10]: 相距L之兩薄透鏡組合
Out[10]: 
⎡-f₂          ⎤
⎢────  f₁ + f₂⎥
⎢ f₁          ⎥
⎢             ⎥
⎢       -f₁   ⎥
⎢ 0     ────  ⎥
⎣        f₂   ⎦

In [11]: h, θ = symbols('h, θ')

In [12]: 平行光 = GeometricRay(h, θ)

In [13]: 平行光
Out[13]: 
⎡h⎤
⎢ ⎥
⎣θ⎦

In [14]: 相距L之兩薄透鏡組合 * 平行光
Out[14]: 
⎡              f₂⋅h⎤
⎢θ⋅(f₁ + f₂) - ────⎥
⎢               f₁ ⎥
⎢                  ⎥
⎢      -f₁⋅θ       ⎥
⎢      ──────      ⎥
⎣        f₂        ⎦

In [15]: f, z = symbols('f, z')

In [16]: 行經距離Z = FreeSpace(z)

In [17]: Z處匯聚現象 = 行經距離Z * 相距L之兩薄透鏡組合 * 平行光

In [18]: Z處匯聚現象
Out[18]: 
⎡  ⎛     f₁⋅z     ⎞   f₂⋅h⎤
⎢θ⋅⎜f₁ - ──── + f₂⎟ - ────⎥
⎢  ⎝      f₂      ⎠    f₁ ⎥
⎢                         ⎥
⎢         -f₁⋅θ           ⎥
⎢         ──────          ⎥
⎣           f₂            ⎦

In [19]: