《鞦韆曲》清‧鮑之蕙
芳園四壁花光聞,鞦韆動處朝霞飛。
美人妝成對花立,欲上不上嬌無力。
㩳身一舉穿林梢,流鶯驚起花旛搖。
翩然反側妙容與,隱隱紅潮上眉𡧃。
藕絲裙輭罥游蜂,杏子衫輕濕香雨。
拖煙約霧東風顛,珠翠彷彿雲中斬。
琤瑽仙珮潄嗚玉,蘭香萼綠相齊肩。
紅纏雪腕綵索勁,綠鬆雲髮金釵偏。
小鬢扶下日初轉,徙倚花陰息嬌喘。
栩栩魂猶夢蝶驚,行行足訝蒼苔輭。
美人會得春難駐,不放芳華等閒度。
來日清明風雨多,落紅滿地奈愁何。
盪鞦韆有道乎?
秋千搖蕩千秋已,
春暖花開打韆鞦。
不管己身有無力,
想方設法出枝頭。
借力使力之術而已耶??
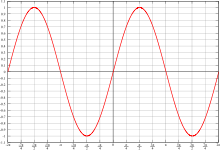
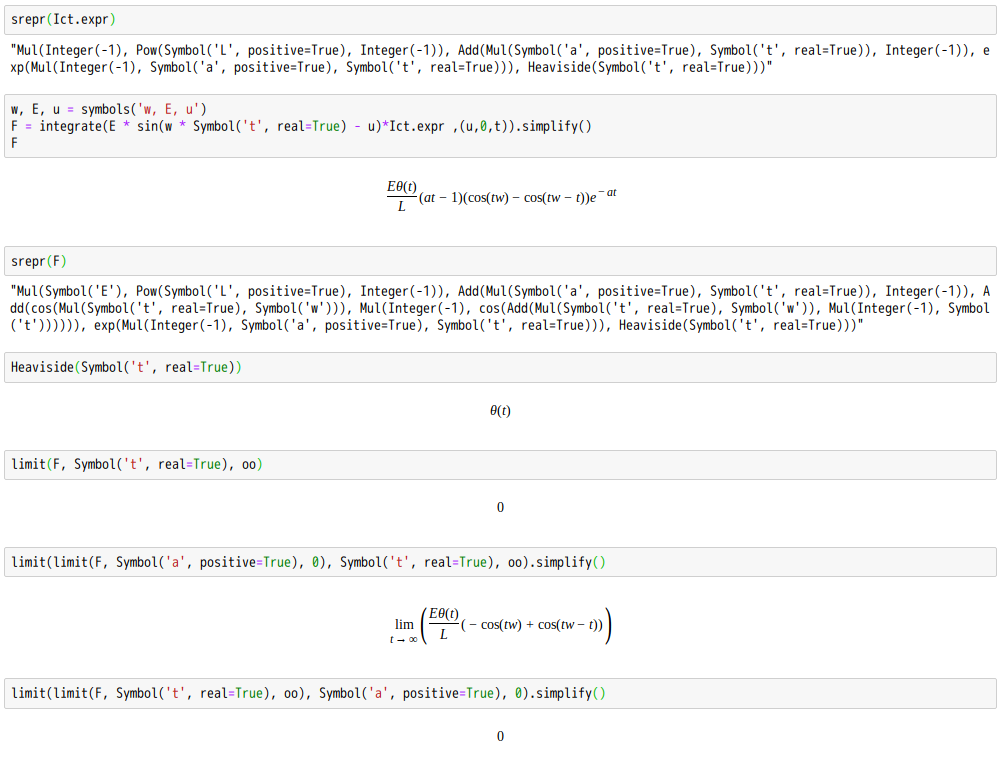
圓周運動的思路,帶給我們另一種考察『受驅振子』系統行為的觀點。在此再次引用《【Sonic π】聲波之傳播原理︰振動篇》一文中的方程式
![]() 是驅動力的振幅大小。在線性微分方程式如
是驅動力的振幅大小。在線性微分方程式如 ![]() 的『求解』裡,如過『
的『求解』裡,如過『![]() 』是
』是 ![]() 的一個解,『
的一個解,『![]() 』是
』是 ![]() 一個『特解』,那麼『
一個『特解』,那麼『![]() 』就是該方程是的『通解』。我們已經知道
』就是該方程是的『通解』。我們已經知道 ![]() 的『低阻尼振子』之解在若干個弛豫時間後數值將變得太小了,所以它對於系統長時間之後的『行為』沒有太多的貢獻。因此我們說這個系統的『穩態解』steady-state solution 是
的『低阻尼振子』之解在若干個弛豫時間後數值將變得太小了,所以它對於系統長時間之後的『行為』沒有太多的貢獻。因此我們說這個系統的『穩態解』steady-state solution 是
![]() ,此處
,此處
![]()
是『響應阻抗』函數。而 ![]() 是驅動力引發的相位角,可由
是驅動力引發的相位角,可由
![]()
所決定,一般它表達著相位『遲滯』 lag 現象。
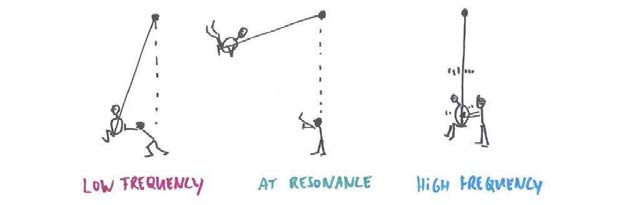
從圓周運動觀點來看,力的最『有效運用』只在於『克服阻力』,不論對抗或者協同『虎克力』,就是要改變系統的『自然振動』之頻率,因此『頻率偏離』愈大愈『多勞少功』。![]() 一式就是這個度量,它在
一式就是這個度量,它在 ![]() 時為『零』。試著幫一個『盪鞦韆』的小女孩『越盪越快』,就可以體驗這和『越盪越高』是很不相同的一回事 !!
時為『零』。試著幫一個『盪鞦韆』的小女孩『越盪越快』,就可以體驗這和『越盪越高』是很不相同的一回事 !!
─── 《STEM 隨筆︰古典力學︰動力學【五‧一】》
那麼
這個系統的『穩態解』steady-state solution 是
![]() ,此處
,此處
![]()
是『響應阻抗』函數。而 ![]() 是驅動力引發的相位角,可由
是驅動力引發的相位角,可由
![]()
所決定,一般它表達著相位『遲滯』 lag 現象。
到底怎麼來的呢?
尚請思考哩!
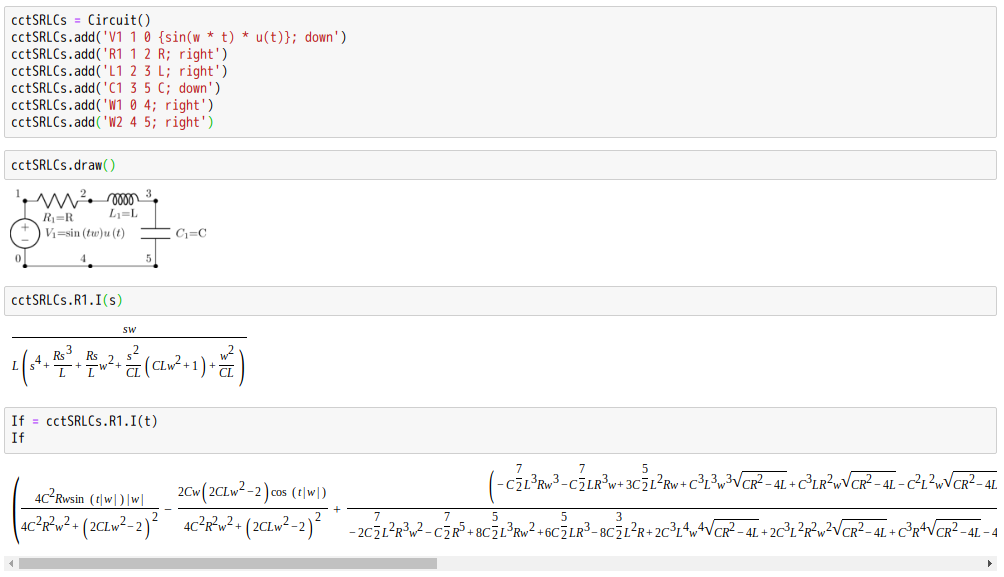
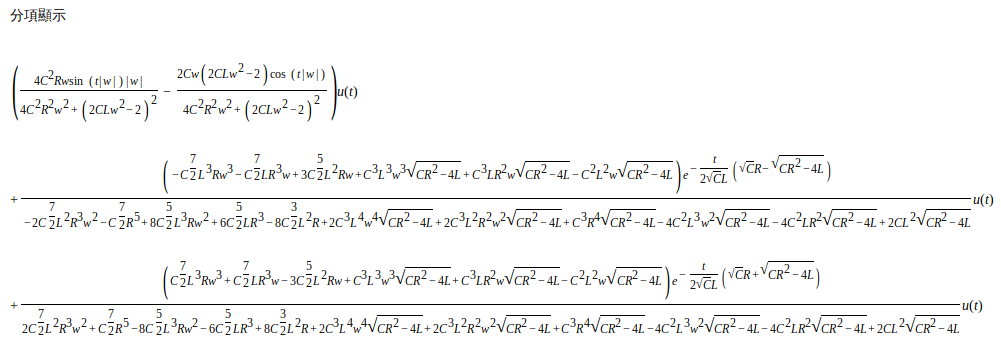
切莫忘卻基本功呦!!