每日彙整: 2018-08-11

樹莓派、樹莓派之學習、樹莓派之教育

STEM 隨筆︰古典力學︰轉子【五】《電路學》 五【電感】 IV‧馬達‧二‧C

當人們在自然中的發現了一些『經驗定律』，有時並不代表我們『知道』它的『成因』。從科學史來看，許多的『物理概念』都是逐步建立起來的。『熱力學第一定律』是『能量守恆』定律對『非孤立系統』的擴展。此時能量可以用『功』 W 或『熱』 Q 的形式傳入或傳出系統。即：

\qquad \mathrm \Delta E_{\rm int}= Q + W

此處 \Delta E_{\rm int} 為『系統內能』的變化量，如果外界對此系統做功，則 W 取正值，反之為取負值。

對於『準靜態』的『可逆過程』，可以寫成微分形式

\qquad \mathrm dE_{\rm int} = \delta Q + \delta W

。一直要到『統計力學』之後，人們才能夠用『微觀粒子』間的『交互作用』來說明這些『現象』的『經驗定律』之『成因』。

假使將『電磁學』與『動力學』聯合起來看，『勞侖茲力定律』Lorentz force law 就十分重要。這個定律是一個『基本公理』，並不能夠從別的理論推導出來，而是由無數次『重複的實驗』所得到之結果。在『電動力學』裡，『勞侖茲力』是一個『帶電粒子』於電磁場中運動時，所感受到的電磁作用力。可以用方程式表達為

\mathbf{F} = q (\mathbf{E} +\mathbf{v} \times \mathbf{B})

此處，\mathbf{F} 是『勞侖茲力』，q 是帶電粒子的『電荷量』，\mathbf{E} 是『電場』，\mathbf{v} 是帶電粒子的『速度』，\mathbf{B} 是『磁場』。

之前我們談到過《德汝德模型》，那麼是否可以用它來解釋『焦耳定律』的呢？回顧前文，德汝德將『導體』想像成由相對固定的『正離子』與可移動的『自由電子』所構成。這些為數眾多的『自由電子』彼此間不斷的發生『碰撞』，又和固定的『正離子』間也發生碰撞。同時德汝德假設了︰

一、如果沒有外部的『電磁場』作用，『自由電子』將會作『直線運動』，彼此間的『電磁作用力』可以被忽略。這意味著是一種『獨立電子』的假設，它處於一個由『正離子』與『其他電子』所構成的『平均的環境』 ── 因此淨作用為零 ──，統計上來講這一般認為是『合宜的』。

二、『電子』和『正離子』之間的『碰撞』是『即時』的，統計上無關之『隨機事件』，所以總體來說這沒有任何『淨貢獻』，雖然有不同的學者『批評』它的『合宜性』。然而如果從『散射事件』來看，這也許只是說某些『物質屬性』之『均向性』的另一種說法罷了。

三、假設了『平均碰撞時間』 \tau 的『存在』，所以我們可以說很小的一段時距 \delta t 發生『碰撞』的『機會』是 \frac {\delta t}{\tau}，而且這個『機率』和一個『自由電子』的『位置』與『動量』無關。這正像是『丟一根』長度為 \delta t 的『針』投到一個以 \tau 為『格子線』板子上，問『針』掉到『線上』的『機率』大小如何，通常被認為是很好的『近似』。

四、『碰撞』後的『熱電子』應該保有該處『熱平衡』的速度。這是一個作用『鄰近原則』的假設，一般從『物理因果』上講，以為應是『正確的』。

事實在『假設二』中的『電子』與『正離子』的『散射碰撞』，是一種『能量不守恆』的碰撞，『電子』將部份的『能量』移轉給了『正離子』，並使得『金屬』溫度上升，這說明了『焦耳定律』的由來。依據『假設三』，一個電子在很小時距 \delta t 發生碰撞的機率是 P_c = \frac{\delta t}{\tau}，那麼某個電子從一開始 0 到 t 時刻不發生碰撞的機率可以這樣計算︰將 0 到 t 時距切割成 N 小段，每一段長 \delta t，如此 t = N \delta t。於是

P_{nc}(t) = \lim \limits_{\delta t \rightarrow 0} \left( 1 - \frac{\delta t}{\tau} \right) \cdots \left( 1 - \frac{\delta t}{\tau} \right) = \lim \limits_{\delta t \rightarrow 0} {\left( 1 - \frac{\delta t}{\tau} \right)}^N

= \lim \limits_{\delta t \rightarrow 0} {\left( 1 - \frac{\delta t}{\tau} \right)}^{\frac{t}{\delta t} } = \lim \limits_{- \frac{\delta t}{\tau} \rightarrow 0} {\left[ {\left( 1 - \frac{\delta t}{\tau} \right)}^{- \frac{\tau}{\delta t}} \right]}^{- \frac{t}{\tau}} = e^{- t/ \tau}

，如此 P_{nc} \cdot P_c = e^{- t/ \tau} \frac{dt}{\tau} 就是間隔了 t 時間，t + dt 時發生碰撞的機率。

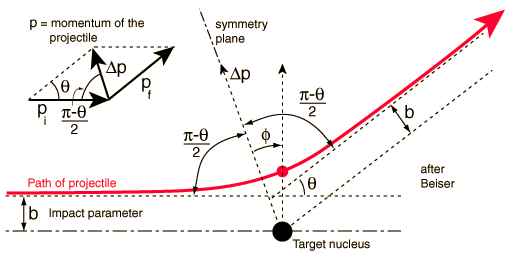
Scattering

 

參考上圖，一個電子以『初始動量』 \vec{p} = m \cdot \vec{v} 在電場 \vec{E} 中作運動，並於 t 時間後與正離子發生碰撞，在發生碰撞前，電子將以 \vec{a} = \frac{\vec{E} e t}{m} 作加速，它的速度將會是 \vec{v_i} = \vec{v} + \Delta \vec{v} = \vec{v} + \vec{a} t = \vec{v} + \frac{\vec{E} e t}{m}。然後與正離子發生碰撞，依據『假設二』，這個『散射現象』是統計上無關的『隨機事件』，於是每一『立體角』Solid angle d \Omega 方向的『散射機率』 \frac{d \Omega}{4 \pi} = \sin(\theta) d \theta d \Phi / 4 \pi 都相等。再按造『假設四』，散射後的速度 | \vec{v_f} | = | \vec{v} |，這個 v 就是電子的『熱速度』。因此這個電子移轉給正離子的能量是

\Delta E(\theta, \Phi) = \frac{1}{2} m ({v_i}^2 - {v_f}^2) = \frac{1}{2} m ({v_i}^2 - v^2)

= \frac{1}{2} m [ ( v^2 + {\Delta v}^2 + 2 v \Delta v \cos{\theta} - v^2 ]

= \frac{{(e E t)}^2}{2 m} + v E e t \cos{\theta}

。各方向的平均移轉能量為

\Delta E = \int \frac{d \Omega}{4 \pi} \Delta E(\theta, \Phi)

= \frac{1}{4 \pi} \int_{0}^{ 2 \pi} d \Phi \int_{0}^{\pi} \sin(\theta) d \theta \Delta E(\theta, \Phi) = \frac{{(e E t)}^2}{2 m}

。如果計之以 P_c \cdot P_{nc} 的機率，如此每個電子每次碰撞，平均的能量損失是

\langle \Delta E \rangle = \int_{0}^{\infty} \frac{d t}{\tau} e^{- t/ \tau} \Delta E = \int_{0}^{\infty} \frac{d t}{\tau} e^{- t/ \tau} \frac{{(e E t)}^2}{2 m} = \frac{{(e E \tau)}^2}{m}

，假使這個導體的『電子密度』是 n，電子的『碰撞頻率』是 \frac{1}{\tau}，單位時間移轉給正離子的平均總能量密度為

\langle \Delta E \rangle \cdot n \cdot \frac{1}{\tau} = \frac{n e^2 \tau}{m} E^2 \equiv \sigma E^2

。如此一根長度是 L，截面積為 A 的導線，單位時間的能量損失就會是

P = A L \cdot \sigma E^2 = \sigma E^2 A L

。在『德汝德模型』中，J = \sigma E，所以 I = J A = \sigma E A，於是

I^2 R = {(\sigma E A)}^2 \cdot \frac{L}{\sigma A} = \sigma E^2 A L = P。

─── 《【SONIC Π】電聲學之電路學《一》中》

 

一個好的『模型』可以開闊眼界，進一步解釋『現象成因』，於是對『經驗定律』，比方說︰

焦耳加熱

焦耳加熱也稱為歐姆加熱或電阻加熱，是電流通過導體產生熱量的過程。

焦耳定律或焦耳-楞次定律是定量說明傳導電流將電能轉換為熱能的定律。 1841 年，英國物理學家詹姆斯·焦耳發現載流導體中產生的熱量 Q（稱為焦耳熱）與電流I的平方、導體的電阻 R 和通電時間 t成比例。而在1842年時，俄國物理學家海因里希·楞次也獨立發現上述的關係，因此也稱為「焦耳－楞次定律」。

採用國際單位制時，焦耳定律的表達式為：

Q = I2Rt 或 P = I2R

其中 Q（熱量）、 I（電流）、 R（電阻）、 t（時間）、 P（熱功率）各量的單位依次為焦耳、安培、歐姆、秒和瓦特。

焦耳定律是設計電照明，電熱設備及計算各種電氣設備溫升的重要公式。

 

也能有更深刻之認識也！或將理解『能量』就是『能量』乎？

只不過『能量』很多種，『單位』常又不同，彼此間形態轉換式子往往費疑猜哩！！

220px-Papin's_digester

220px-Pressure_cooker_manufactured_by_Georg_Gutbrod,_Stuttgart,_about_1864

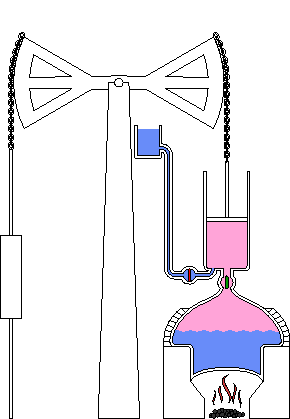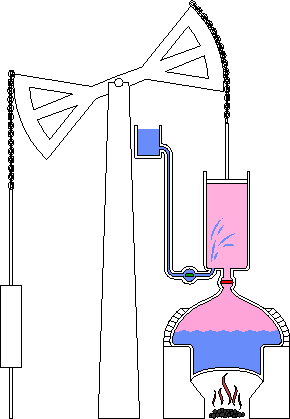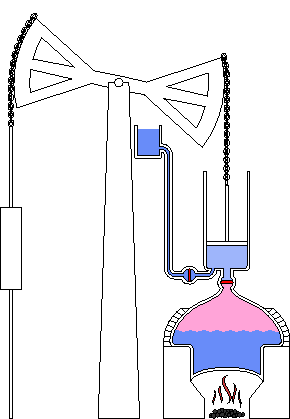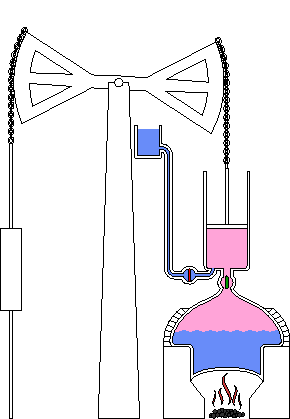
Newcomen_atmospheric_engine_animation

220px-Watt_James_von_Breda
功率的單位是瓦特

100px-Watts_First_Condenser

220px-Watt_apparatus_3

SteamEngine_Boulton&Watt_1784

220px-20070616_Dampfmaschine

220px-Loughborough_Beam_Engine_-_geograph.org.uk_-_2734519

一六七三年法國物理學家丹尼斯‧帕潘 Denis Papin 在巴黎與惠更斯和萊布尼茨做助手期間，逐漸對利用『真空』產生動力感到興趣。其後在為波義耳做助手期間，發明了『高壓蒸鍋』 steam digester，這是一個氣密性良好，藉著增大氣壓提高水的沸點，能夠達到縮短烹飪時間的目的，是『蒸汽機』和『壓力鍋』的前身。一六八一年，帕潘將他的發明帶到了倫敦的英國皇家學會，最終這個發明被當作了一個『實驗器材』；不過，還是給了他加入學會的資格。然而一七零七年到一七一二年間，帕潘多篇論文被皇家學會發表，非但沒有通知他本人，也都沒有付稿費，這令他極為不滿。傳聞帕潘實於一七一二年裡，在窮困潦倒中去世，死後葬於一個不知名的地方。

同一年一七一二年，英國工程師和發明家湯瑪斯‧紐科門 Thomas Newcomen 發明利用『蒸氣』作『機械功』的『氣壓引擎』atmospheric engine，今天稱之為『紐科門蒸氣引擎』，之後被運用在礦區與油田，以節省大量的人力。

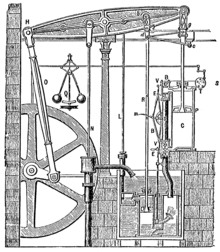
蘇格蘭著名的發明家和機械工程師詹姆斯‧馮‧布雷達‧瓦特 James von Breda Watt 是英國皇家學會院士，愛丁堡皇家學會院士。瓦特小時候因為身體孱弱去學校的時間不多，主要的教育都是由母親在家裡進行。他從小就表現出了靈巧的雙手以及數學上的天分，喜歡很多蘇格蘭的民間傳說與故事。一七歲時母親過世，而父親的生意又開始走下坡。瓦特於是到倫敦的一家儀錶修理廠作了一年的徒工，然後回到蘇格蘭格拉斯哥打算開一家自己的修理店。儘管當時蘇格蘭還沒有類似的修理店，由於他並沒有做滿所要求的七年徒工，他的開店申請還是被格拉斯哥的錘業者行會拒絕了。一七五七年格拉斯哥大學的教授給瓦特一個機會，讓他在大學裡開設了一間小修理店，這幫助了他走出了困境。當時物理學家與化學家約瑟夫‧布萊克 Joseph Black 教授更成了瓦特的朋友與導師 。瓦特的小店開業四年後，在朋友蘇格蘭物理學家和發明家約翰‧羅比遜 John Robison 引導下，瓦特開始了對蒸汽機的實驗。據聞那時瓦特也還從未親眼見過一台可以運轉的蒸汽機，但是他就開始建造自己的蒸汽機模型。起初的實驗失敗後，他堅持繼續實驗並且閱讀了所有他能找到的有關蒸汽機的文獻 ，而且獨立的發現了『潛熱』的重要性，殊不知這早在多年前就已被布萊克教授所發現的了。

一七六三年，瓦特得知格拉斯哥大學有一台紐科門蒸汽機 Newcomen steam engine，然而正在倫敦修理，他請求學校取回了這台蒸汽機並親自進行了修理。雖然經過修理，這台蒸汽機勉強可以工作，但是效率很低。再藉著大量的實驗，瓦特發現效率低的原因是因為活塞每推動一次，氣缸里的蒸汽都要先行冷凝，然後再加熱進行下一輪推動，這使得蒸汽百分之八十的熱量，都耗費在為了維持氣缸的溫度之上。一七六五年瓦特取得了關鍵性的進展，他將冷凝器與氣缸分離開來 ，使得氣缸溫度可以持續維持在注入之蒸汽的溫度，並在此基礎上很快建造了一個可以運轉的模型。……這就是 瓦特發明蒸汽機的故事！！

 

瓦特改良了紐科門蒸汽機，這事奠定了『工業革命』的重要基礎，他是那個時代裡的重要人物。 瓦特創造『馬力』的概念，後人為了紀念他的貢獻，便將『功率』的『單位』命名為『瓦特』。

有些人認為『工業革命』始於一七五九年左右，但是直到一八三零年代，它還沒有真正蓬勃的展開。普遍的觀點認為，工業革命發源於英格蘭中部地區，是在一七六九年瓦特改良蒸汽機之後，再因為一系列『技術革命』引發了從『手工勞動』朝向由『機器生產』的轉變，是一次『生產方式』的重大飛躍。隨後才自英格蘭擴散到整個歐洲大陸，一九世紀方傳播到了北美地區。由於『工業革命』是以機器取代人力，以大規模『工廠化生產』取代個體作坊『手工生產』的一場『生產』與『科技』之革命。因此機器的發明及運用成為了這個時代的標誌，所以歷史學家稱這個時代為『機器時代』 the Age of Machines。

自然界中『能量』的『形式』有很多種，不同的『學說‧理論』的歷史的發展，產生了能量的多種『單位』︰

【機械功】︰ \int \vec{F} \cdot \vec{ds} 是『牛頓‧米』，一『『牛頓‧米』就是一『焦耳』。

【熱能』︰將一公克的水在一大氣壓 ── 101.325 kPa ── 下升高攝氏一度所需要的熱量，叫做一『卡路里』Calorie，簡稱作『卡』，縮寫成 cal。後來的科學家發現水在不同溫度下的比熱容量不同，所以又衍生了許多不同的定義。這就是焦耳所量測的『熱功當量』。一『卡』等於  4.186 『焦耳』。

『電能』︰依據『焦耳定律』 I \cdot V \cdot t 是『安培‧伏特‧秒』，也就是說一『安培‧伏特‧秒』就是一『焦耳』。

所謂的『功率』 power 是指『能量』之『轉換』或者『使用』的『速率』，用單位時間的能量大小來表示。『功率』的『單位』是『瓦特』 W ，假使 \Delta W 是一物理系統在 \Delta t 時間內所做的功，那麼這段時間內的『平均功率』 P_{avg} 可以由下式給出

P_{avg} = \frac{\Delta W}{\Delta t}

。而『瞬時功率』就是當時間 \Delta t \rightarrow 0 時，『平均功率』的極限值

P = \lim \limits_{\Delta t\to 0} \frac{\Delta W}{\Delta t} = \frac{{\rm d}W}{{\rm d}t}

。也就是講一秒消耗一焦耳的能量就是一『瓦特』，一般所說的『一度電』是指『一千瓦小時』所使用的『電能』多寡，它等於 1000 \cdot 60 \cdot 60 J。

從『瞬時功率』 的『定義』，可以推導出

【機械瞬時功率】是 {P}(t) = \vec{F}(t) \cdot \vec{v}(t)；

【電力瞬時功率】是 P(t) = I(t) \cdot V(t)。

─── 摘自《【SONIC Π】電路學之補充《二》》

 

因此最好知道所謂的『因次分析』呦？？

為什麼要討論『物理量』的『單位』呢？因為一般物理定律都用著『數學式』表達，萬一所計算的物理量發生了『 1 公斤  + 6 米 – 8 秒 』，這可能要比南宋著名禪宗大師大慧宗杲，是臨濟宗楊岐派第五代傳人，所提倡的『看話禪』── 舉個例說︰『萬法歸一，一歸何處？』── 還要『難參無解』。據說物理量使用單位的『因次分析』dimensional analysis 始於牛頓之『相似性原理』；就建立因次分析的現代意義用法上講，馬克士威是位重要的推手，他區分『質量』 、『長度』、『時間』的度量單位為『基礎單位』，將其它單位歸類為『衍生單位』。十九世紀時法國數學家約瑟夫‧傅立葉 Joseph Fourier 洞悉了『物理定律』的『數學方程式』應當與度量物理量的『單位無關』。難道說一個人用『 □ □ 制』單位，另一個人用『○ ○制』單位，他們的牛頓第二運動定律 \mathbf{F}=m\mathbf{a} 就因此會是『兩種』的嗎？假使兩人描述『同一』自然現象，在彼此使用的『單位換算』後，竟然能夠是『答案不同』的嗎？？

那什麼是物理量的『因次』呢？舉個例子，在 MKS 制中，一般力的『度量單位』是『牛頓』Newton，通常用 N 代表。那你怎麼知道『一牛頓的力』有多大呢？ 其實它有個『定義』︰

1 N \equiv_{df} 使質量 1 kg 物體的加速度為 1 \frac{m}{s^2}} 時所需要的力

。那麼這個定義又從哪裡來的呢？它就是從牛頓第二運動定律 F = m \cdot a 來的，因此 F 之『N』那個單位與 m \cdot a 的『kg \cdot \frac{m}{s^2}}』這個度量單位，都是表達牛頓第二運動定律中『力』、『質量』和『加速度』的『概念』間的『物理量』的『單位度量關係』。由於我們是從『質量』和『加速度』的基礎物理量之『大小』，來定義『力的單位』，所以說『牛頓』是一個衍生的『導出單位』。如果比較 CGS 制『一達因的力』之『定義』

1 dyne \equiv_{df} 使質量 1 g 物體的加速度為 1 \frac{cm}{s^2}} 時所需要的力

，所以 1 N = 1 \frac{kg \cdot m}{s^2}} = \frac{1000 g \cdot 100 cm}{s^2}} = 10^5 \frac{g \cdot cm}{s^2}} = 10^5 dyne

。仔細考察『單位轉換』的過程，『1 kg = 1000 g』，而『kg, g』都是『質量度量』單位，同樣的『1 m = 100 cm』中之『m, cm』都是『長度度量』單位。由於『自然界』並沒有偏好哪一種『度量單位』，它的選擇當然是『人為的』。其次『相同』的『度量領域』的『單位變換』，它的『變換係數』通常是無單位的數值『常數』，比方說『1 m = {10}^2 cm』中之『{10}^2』，或者『1 kg = {10}^3 g』裡的『{10}^3』，因為它們都是同類的度量單位。於是我們可以說『因次』就是『物理單位』中『物理概念』的『度量抽象』。舉例來講，不論長度的度量單位是『米、公分、尺、…』 ，我們都說這個『物理量』的『因次』是『長度』。這樣一個物理量的因次就可以由是基本的『質量』、『長度』、『時間』、『電荷量』、『絕對溫度』…組合，藉由對應的『因次符號』『M』、『L』、『T』、『Q』、『\Theta』…來表達，將該物理量的因次寫成『 M^{q_1} \cdot L^{q_2} \cdot T^{q_3} \cdot Q^{q_4} \cdot {\Theta}^{q_5} \cdots』，此處的 q_1, q_2, q_3, \cdots 都是『有理數』。

假使說發現了一個物理定律，就說是『彈簧』的『虎克定律』F = k \cdot x 吧，那麼虎克常數『k』的因次是什麼呢？如果將這個線性彈簧施加『1 N』的力，它從平衡處位移了『\alpha \cdot m』，此處 \alpha 是『無因次』的『純量』。這樣依據『虎刻定律』

1 N = 1 kg \cdot \frac{m}{s^2}} = k \cdot \alpha \cdot m

，因此 k = {\alpha}^{-1} \frac{kg}{s^2}}，k 的因次是 M \cdot T^{-2}，也許有人想還是『牛頓/米』比較親切的啊！這個『每秒每秒幾公斤』到底是什麼的嗎？？事實上『自然定律』將各個『物理概念』聯繫了起來，於是『同類現象』或者『運動現象』在『度量上』需要與『已經定義』的『單位』保有『一致性』，能夠彼此『相容』。就像牛頓的『萬有引力』定律 F = G \frac{m_1 m_2}{r^2}，既然是『力的範疇』，那個『萬有引力常數』G

G = \left(6.67384 \plusmn 0.00080 \right) \times 10^{-11} \ \mbox{m}^3 \ \mbox{kg}^{-1} \ \mbox{s}^{-2}

的『單位』就得確保最終 G \frac{m_1 m_2}{r^2} 是『力』的單位，而且符合『一牛頓的力』度量之大小『定義』。當然它的因次 L^3 \cdot M^{-1} \cdot T^{-2} 就是『抽象』的了！要是說道兩靜電荷間作用力的『庫侖定律』

F = k_{\mathrm{e}}\frac{qq'}{r^2} ，
k_{\mathrm{e}} = 8.987\ \times 10^9 \ \mathrm{N \cdot m^2 \cdot C^{-2}}

，就怕那個『庫侖常數』 k_{\mathrm{e}} 的『因次』 M \cdot L^3 \cdot T^{-2} \cdot Q^{-2} 會是『天書』的吧！其實這卻是許多『物理常數』的由來！！

─── 摘自《【SONIC Π】聲波之傳播原理︰原理篇《四上》》

 

如是藉著

歐拉運動定律

歐拉運動定律（Euler’s laws of motion）是牛頓運動定律的延伸，可以應用於多粒子系統運動或剛體運動，描述多粒子系統運動或剛體的平移運動、旋轉運動分別與其感受的力、力矩之間的關係 。在艾薩克·牛頓發表牛頓運動定律之後超過半個世紀，於1750年 ，萊昂哈德·歐拉才成功地表述了這定律。[1][2]

剛體也是一種多粒子系統，但理想剛體是一種有限尺寸，可以忽略形變的固體。不論是否感受到作用力，在剛體內部，點與點之間的距離都不會改變。

歐拉運動定律也可以加以延伸，應用於可變形體（deformable body）內任意部分的平移運動與旋轉運動。

剛體

歐拉第一運動定律

歐拉第一定律表明，從某慣性參考系觀測，施加於剛體的淨外力 ，等於剛體質量與質心加速度的乘積。[3]歐拉第一定律以方程式表達為

\displaystyle \mathbf {F} ^{(ext)}=m\mathbf {a} _{cm}

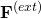其中，\displaystyle \mathbf {F} ^{(ext)} 是剛體感受到的淨外力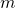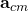，\displaystyle m 、 \displaystyle \mathbf {a} _{cm} 分別是剛體的質量、質心加速度。

剛體的平移運動等同於位於其質心、具有其質量的粒子，感受到同樣的淨外力，而呈現的運動。

……

歐拉第二運動定律

歐拉第二定律表明，設定某慣性參考系的固定點O（例如，原點）為參考點，施加於剛體的淨外力矩，等於角動量的時間變化率。歐拉第二定律以方程式表達為

\displaystyle {\boldsymbol {\tau }}_{O}^{(ext)}={\frac {\mathrm {d} \mathbf {L} _{O}}{\mathrm {d} t}} ；

其中，\displaystyle {\boldsymbol {\tau }}_{O}^{(ext)} 是對於點O淨外力矩，\displaystyle \mathbf {L} _{O} 是對於點O的角動量。

……… 摘自《STEM 隨筆︰古典力學︰動力學》

※ 註︰

角動量

在物理學中，角動量是與物體的位置向量和動量相關的物理量。對於某慣性參考系的原點 \displaystyle \mathbf {O} ，物體的角動量是物體的位置向量和動量的叉積，通常寫做 \displaystyle \mathbf {L} 。角動量是向量。

\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p}

其中， \displaystyle \mathbf {r} 表示物體的位置向量， \displaystyle \mathbf {L} 表示角動量。 \displaystyle \mathbf {p} 表示動量。角動量 \displaystyle \mathbf {L} 又可寫為：

\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p} =\mathbf {r} \times (m\mathbf {v} )=\mathbf {r} \times (m\times (r{\boldsymbol {\omega }}))=mr^{2}{\boldsymbol {\omega }}=I{\boldsymbol {\omega }}

其中， \displaystyle I 表示杆狀系統的轉動慣量， \displaystyle {\boldsymbol {\omega }} 是角速度向量。

假設作用於物體的外力矩和為零，則物體的角動量是守恆的。需要注意的是，由於成立的條件不同，角動量是否守恆與動量是否守恆沒有直接的聯繫。

當物體的運動狀態（動量）發生變化，則表示物體受力作用，而作用力大小就等於動量 \displaystyle \mathbf {P} 的時變率： \displaystyle \mathbf {F} ={\frac {d\mathbf {P} }{dt}}

當物體的轉動狀態發生改變時，表示物體受到力矩作用，而力矩就等於角動量的時變率： \displaystyle {\boldsymbol {\tau }}={\frac {d\mathbf {L} }{dt}}

 

當曉 \vec{\tau} (t) \cdot \vec{\omega} (t) 是瞬時功率耶☆