一個『實數函數』![]() 在某一點
在某一點 ![]() 的『極限值』假設是
的『極限值』假設是 ![]() ,可以記作
,可以記作 ![]() ,如果用『超實數』來『定義』就是
,如果用『超實數』來『定義』就是 ![]() 。
。 ![]() 的『極限觀』假使從『空間度量』的觀點來看,任一個
的『極限觀』假使從『空間度量』的觀點來看,任一個 ![]() 所指定的是『函數』
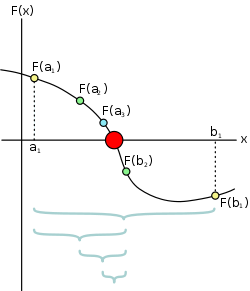
所指定的是『函數』 ![]() 的『對應域』中的一個『開區間』
的『對應域』中的一個『開區間』 ![]() ,問著『定義域』中是否存在一個『開區間』
,問著『定義域』中是否存在一個『開區間』 ![]() ,使得
,使得 ![]() 。如果我們取
。如果我們取 ![]() ,這些
,這些 ![]() 將會『疊套逼近』於
將會『疊套逼近』於 ![]() 點,然而
點,然而 ![]() 所對應的
所對應的 ![]() 卻未必然形成一個『收斂於』
卻未必然形成一個『收斂於』 ![]() 點之『疊套區間』!這是為什麼的呢?考慮
點之『疊套區間』!這是為什麼的呢?考慮 ![]() ,對於任何的
,對於任何的 ![]() 來講,
來講,![]() 必然的成立,於是這個函數的整個『定義域 』,都可以滿足『極限』的『定義』,此時
必然的成立,於是這個函數的整個『定義域 』,都可以滿足『極限』的『定義』,此時 ![]() 的那個
的那個 ![]() 與
與 ![]() 根本沒有關係,我們又要如何去說那個
根本沒有關係,我們又要如何去說那個 ![]() 的呢?也就是說
的呢?也就是說 ![]() 的『極限觀』是從『函數』的『對應域』或者說『值域』來論證『極限』的『存在性』。而『超實數』的『極限觀』
的『極限觀』是從『函數』的『對應域』或者說『值域』來論證『極限』的『存在性』。而『超實數』的『極限觀』 ![]() ,是從『函數』的『定義域』直接探討『極限』的『存在性』。這兩個『觀點』果真能『互證』的嗎?從『超實數』的『極限觀』來看雖然前述所說的
,是從『函數』的『定義域』直接探討『極限』的『存在性』。這兩個『觀點』果真能『互證』的嗎?從『超實數』的『極限觀』來看雖然前述所說的 ![]() 可以有各種『選擇』, 自然就包含了
可以有各種『選擇』, 自然就包含了 ![]() 這種選擇,因此依然是
這種選擇,因此依然是 ![]() 的啊!
的啊!
也就是說,如果我們用 ![]() 『極限觀』下的
『極限觀』下的 ![]() 所對應的
所對應的 ![]() 構造一個『開區間』
構造一個『開區間』 ![]() ,那麼就有
,那麼就有 ![]() ,這就是『超實數』的『極限觀』
,這就是『超實數』的『極限觀』 ![]() 。反過來說假使『超實數』的『極限觀』也可以證明
。反過來說假使『超實數』的『極限觀』也可以證明 ![]() 『極限觀』的話,這兩種『觀點』就在『邏輯』上『等價』,也就是說無論『擇取』那一種,就『實數分析』來講,所得到的『結論』,都是一樣的。就讓我們證明它的『對偶命題』吧︰如果否定
『極限觀』的話,這兩種『觀點』就在『邏輯』上『等價』,也就是說無論『擇取』那一種,就『實數分析』來講,所得到的『結論』,都是一樣的。就讓我們證明它的『對偶命題』吧︰如果否定 ![]() 『極限觀』可以推導出否定『超實數』的『極限觀』。
『極限觀』可以推導出否定『超實數』的『極限觀』。
假使有一個 ![]() ,對於所有的『正實數』
,對於所有的『正實數』 ![]() ,都有
,都有 ![]() 而且
而且 ![]() 。因此這個『陳述』對『疊套區間』
。因此這個『陳述』對『疊套區間』 ![]() 而言也成立,也就是說
而言也成立,也就是說 ![]() 時
時 ![]() ,這與
,這與 ![]() 『矛盾』,於是否定了『超實數』的『極限觀』,所以『對偶命題』成立。為什麼我們採取證明『對偶命題』的呢?因為『所有的有一個』
『矛盾』,於是否定了『超實數』的『極限觀』,所以『對偶命題』成立。為什麼我們採取證明『對偶命題』的呢?因為『所有的有一個』 ![]() 之類的『命題』是很難『直接論證』的,通常它的『否定命題』
之類的『命題』是很難『直接論證』的,通常它的『否定命題』 ![]() 比較容易『論述』,於是我們如是選擇。事實上這也說明了『標準分析』為什麼常常讓初學者『頭大』的原因,以及『懷疑』真的能從『一點之鄰域』可以『議論』那個『極限值』的嗎?就像俗語說的︰千里來龍,在此結穴,就『無窮逼近』來講,所有的『有限量』無論它有多大,並不會改變這個『有限性』,因此總得越來越靠近所『論述』之『點』,然而儘管再近再近也都還未能到『無窮小』之『距離』,更不要講任何一個給定的有限『開區間』都能與整個『實數系』產生『一一對應』是屬於同等級的『無限大』。這就是雖然『直觀上』當
比較容易『論述』,於是我們如是選擇。事實上這也說明了『標準分析』為什麼常常讓初學者『頭大』的原因,以及『懷疑』真的能從『一點之鄰域』可以『議論』那個『極限值』的嗎?就像俗語說的︰千里來龍,在此結穴,就『無窮逼近』來講,所有的『有限量』無論它有多大,並不會改變這個『有限性』,因此總得越來越靠近所『論述』之『點』,然而儘管再近再近也都還未能到『無窮小』之『距離』,更不要講任何一個給定的有限『開區間』都能與整個『實數系』產生『一一對應』是屬於同等級的『無限大』。這就是雖然『直觀上』當 ![]() 越來越靠近
越來越靠近 ![]() ,要是
,要是 ![]() 不靠近
不靠近 ![]() ,或者就『連續函數』來講
,或者就『連續函數』來講 ![]() 難到是『可能的』嗎?如果從這裡的『等價證明』來說,這是『不可能的』!那麼假使一個『函數』
難到是『可能的』嗎?如果從這裡的『等價證明』來說,這是『不可能的』!那麼假使一個『函數』 ![]() 在
在 ![]() 時有『定義』而且『連續』,就一個『無窮小數』
時有『定義』而且『連續』,就一個『無窮小數』 ![]() 而言,
而言, ![]() 能夠不是一個『無窮小數』 的嗎??
能夠不是一個『無窮小數』 的嗎??