當我們說『超實數體』 ![]() 中的『無窮小』量『取消』了『實數』的『阿基米德性』時,這是針對一個『超實數』的『無窮小』量
中的『無窮小』量『取消』了『實數』的『阿基米德性』時,這是針對一個『超實數』的『無窮小』量 ![]() 部分說的,就像對一個『複數』
部分說的,就像對一個『複數』 ![]() 來講,只有『虛數部分』
來講,只有『虛數部分』 ![]() , 而
, 而 ![]() 一樣。為什麼要取消呢?因為
一樣。為什麼要取消呢?因為 ![]() 的『倒數』
的『倒數』 ![]() 就是『無限大』,如果『無窮小』數滿足『阿基米德性質』的話,那麼就會有一個『夠大』的數
就是『無限大』,如果『無窮小』數滿足『阿基米德性質』的話,那麼就會有一個『夠大』的數 ![]() 使得
使得 ![]() ,於是
,於是 ![]() ,這就產生了『矛盾』的啊!在數學上常用著『歸謬證法』,並非總是因為人們不能夠『直接證明』某個『陳述』,故而採取『迂迴』的辦法,就像說因為已經定義了『有理數』是種『分數』,可以用兩個『整數』
,這就產生了『矛盾』的啊!在數學上常用著『歸謬證法』,並非總是因為人們不能夠『直接證明』某個『陳述』,故而採取『迂迴』的辦法,就像說因為已經定義了『有理數』是種『分數』,可以用兩個『整數』 ![]() 表達成
表達成 ![]() 的『形式』,因此如果一個數
的『形式』,因此如果一個數 ![]() 『不是』有理數,將之稱作『無理數』,就是講
『不是』有理數,將之稱作『無理數』,就是講 ![]() 『不可能』表達成
『不可能』表達成 ![]() 的『形式』,於是要證明這個
的『形式』,於是要證明這個 ![]() 是『無理數』,就轉變成了證明它『不可能』表達成
是『無理數』,就轉變成了證明它『不可能』表達成 ![]() 的『形式』,或者說『歸謬』的證明『假設』它『可以』表達成
的『形式』,或者說『歸謬』的證明『假設』它『可以』表達成 ![]() 的『形式』,就一定會產生『邏輯矛盾』的了。比方講『
的『形式』,就一定會產生『邏輯矛盾』的了。比方講『![]() 是無理數』的證明
是無理數』的證明
『假設』 ![]() 是有理數,可以寫成無公因數的最簡分數
是有理數,可以寫成無公因數的最簡分數 ![]() ,也就是
,也就是 ![]() 。所以,
。所以,![]() ,這樣
,這樣 ![]() 就一定是『偶數』,就說
就一定是『偶數』,就說 ![]() 吧,將它代入上式,得到
吧,將它代入上式,得到 ![]() ,這樣 Q 也一定是『偶數』,於是和『假設』矛盾,因此證明了『結論』。
,這樣 Q 也一定是『偶數』,於是和『假設』矛盾,因此證明了『結論』。
於是我們『明白』了 ![]() 不是『有理數』,當然我們也就『知道』了無理數是『存在的』,只不過對
不是『有理數』,當然我們也就『知道』了無理數是『存在的』,只不過對 ![]() 這個數所知甚少,連它的『近似』之大小都不知道。所以人們往往將這一類的『證明』稱之為『存在性證明』,彷彿有些些『貶義』,代表著所知並不夠深入﹐只能夠『知其一』未必就能『知其二』。要是人們可以『建構』出這個數,就『此建構』之同時證明了它的『不可能性』,似乎是『好的多』的吧!比方講從一個『恆等式』
這個數所知甚少,連它的『近似』之大小都不知道。所以人們往往將這一類的『證明』稱之為『存在性證明』,彷彿有些些『貶義』,代表著所知並不夠深入﹐只能夠『知其一』未必就能『知其二』。要是人們可以『建構』出這個數,就『此建構』之同時證明了它的『不可能性』,似乎是『好的多』的吧!比方講從一個『恆等式』
![]() ,我們可以用『連分數』表達作
,我們可以用『連分數』表達作
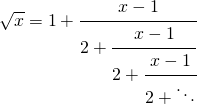
,我們也可以『證明』 ![]() 是『無理數』,它的『證明』卻未必更『容易理解』。因此作者無意於此『優劣度』多作文章,祇是說『存在性證明』 之所以重要在於『確定』這個『論域』不是一個『空集合』 ∅ ,它至少有一個『元素』,也不是一種『虛構』。或許說當『已經知道』了就更容易找到其它『建構方式』也說不定的吧!!
是『無理數』,它的『證明』卻未必更『容易理解』。因此作者無意於此『優劣度』多作文章,祇是說『存在性證明』 之所以重要在於『確定』這個『論域』不是一個『空集合』 ∅ ,它至少有一個『元素』,也不是一種『虛構』。或許說當『已經知道』了就更容易找到其它『建構方式』也說不定的吧!!
一八四四年,法國大數學家『約瑟夫‧劉維爾』 Joseph Liouville 證明了『超越性』 ── 這是指任何一個不是『代數數』 algebraic number 的『無理數』,也就是說它不是任何『有理係數』方程式之『實數解』 ── ,他是第一個證實『超越數』 Transcendental number 之存在的人。據聞他曾經考慮過了這一個數 ![]() ,那麼『這一個數』是不是一個『有理數』的呢?假使就今日所知,如果一個實數
,那麼『這一個數』是不是一個『有理數』的呢?假使就今日所知,如果一個實數 ![]() 滿足,對任何正整數
滿足,對任何正整數 ![]() ,都存在有整數
,都存在有整數 ![]() 而言,其中
而言,其中 ![]() 而且『定然』的會有
而且『定然』的會有 ![]() ,因此我們就將此數
,因此我們就將此數 ![]() 叫做『劉維爾數』來講,那麼
叫做『劉維爾數』來講,那麼 ![]() 這個數就『必然』不得不是一個『超越數』的了。然而一個『超越數』也就是一個『無理數』,而且它還是一個非『代數數』的『無理數』,或許說這也就是『建構方式』的重要性的吧!!
這個數就『必然』不得不是一個『超越數』的了。然而一個『超越數』也就是一個『無理數』,而且它還是一個非『代數數』的『無理數』,或許說這也就是『建構方式』的重要性的吧!!
有人說很容易證明『劉維爾數』一定是個『無理數』。假使它不是一個『無理數』,那麼 ![]() 。 要是取足夠大的
。 要是取足夠大的 ![]() 使得
使得 ![]() ,在
,在 ![]() 時有
時有
![]() ,因此就與它的定義發生矛盾。這樣『劉維爾常數』
,因此就與它的定義發生矛盾。這樣『劉維爾常數』
![]()
是一個『建構的數』,假使 ![]() ,那麼對於所有正整數
,那麼對於所有正整數 ![]()
![]()
![]()
。難道我們真的就能夠論斷它不只是個『無理數』,而且是一個非『代數數』的嗎??