每日彙整: 2017-03-18

樹莓派、樹莓派之學習、樹莓派之教育

時間序列︰生成函數‧漸近展開︰無限大等級 III

無限大 \infty 是『符號』，它不是一個『數』！因此擴展實數線

Extended real number line

 In mathematics, the affinely extended real number system is obtained from the real number system ℝ by adding two elements: + ∞ and – ∞ (read as positive infinity and negative infinity respectively). These new elements are not real numbers. It is useful in describing various limiting behaviors in calculus and mathematical analysis, especially in the theory of measure and integration. The affinely extended real number system is denoted  \overline{\mathbb{R}} or [–∞, +∞] or ℝ ∪ {–∞, +∞}.When the meaning is clear from context, the symbol +∞ is often written simply as ∞.

 

才如是描述它。同樣的無窮小 \delta \epsilon 不過是個『極限』接近『零』 0 之『概念』，它也不是一個『數』！！然而『零』是個『數』，一個滿足 0 < | \delta \epsilon | 的『量』，無有疑議焉？ \lim \limits_{x \to \infty} 0 \cdot x^n = \ 0 \ ?? \ , n >0 。若是考慮 x^{-m} , \ m >0 ，當 x \to \infty 時，就說它叫 m 冪無窮小吧 ，則有

\lim \limits_{x \to \infty} \frac{x^n}{x^m} = \infty , \ if \ m < n ,

\lim \limits_{x \to \infty} \frac{x^n}{x^m} = 1 , \ if \ m = n ,

\lim \limits_{x \to \infty} \frac{x^n}{x^m} = 0 , \ if \ m > n .

。那麼『零』到底是哪種等級的無窮小呢？？！！假使可以構造 \frac{1}{{\infty}^{\infty}} 這種無窮小，比方說 \lim \limits_{x \to \infty} \frac{1}{x^x} ，那麼也能夠產生 { \left( x^x \right) }^{x} , \ x \to \infty 這樣無限大啊！！？？或將能了 0^0 引發的論辯耶︰

Zero to the power of zero

Discrete exponents

There are many widely used formulas having terms involving natural-number exponents that require 00 to be evaluated to 1. For example, regarding b0 as an empty product assigns it the value 1, even when b = 0. Alternatively, the combinatorial interpretation of b0 is the number of empty tuples of elements from a set with b elements; there is exactly one empty tuple, even if b = 0. Equivalently, the set-theoretic interpretation of 00 is the number of functions from the empty set to the empty set; there is exactly one such function, the empty function.[21]

Polynomials and power series

Likewise, when working with polynomials, it is often necessary to assign  0^{0} the value 1. A polynomial is an expression of the form  a_{0}x^{0}+\cdots +a_{n}x^{n} where x is an indeterminate, and the coefficients  a_{n} are real numbers (or, more generally, elements of some ring). The set of all real polynomials in x is denoted by  \mathbb {R} [x]. Polynomials are added termwise, and multiplied by the applying the usual rules for exponents in the indeterminate x (see Cauchy product). With these algebraic rules for manipulation, polynomials form a polynomial ring. The polynomial  x^{0} is the identity element of the polynomial ring, meaning that it is the (unique) element such that the product of  x^{0} with any polynomial  p(x) is just  p(x).[22] Polynomials can be evaluated by specializing the indeterminate x to be a real number. More precisely, for any given real number  x_{0} there is a unique unital ring homomorphism  \operatorname {ev} _{x_{0}}:\mathbb {R} [x]\to \mathbb {R} such that  \operatorname {ev} _{x_{0}}(x^{1})=x_{0}.[23] This is called the evaluation homomorphism. Because it is a unital homomorphism, we have \operatorname {ev} _{x_{0}}(x^{0})=1. That is, x^{0}=1 for all specializations of x to a real number (including zero).

This perspective is significant for many polynomial identities appearing in combinatorics. For example, the binomial theorem  (1+x)^{n}=\sum _{k=0}^{n}{\binom {n}{k}}x^{k} is not valid for x = 0 unless 00 = 1.[24] Similarly, rings of power series require x^{0}=1 to be true for all specializations of x. Thus identities like {\frac {1}{1-x}}=\sum _{n=0}^{\infty }x^{n} and  e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}} are only true as functional identities (including at x = 0) if 00 = 1.

In differential calculus, the power rule {\frac {d}{dx}}x^{n}=nx^{n-1} is not valid for n = 1 at x = 0 unless 00 = 1.

Continuous exponents

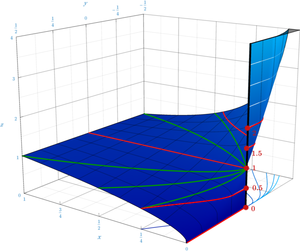
Plot of z = xy. The red curves (with z constant) yield different limits as (x, y) approaches (0, 0). The green curves (of finite constant slope, y = ax) all yield a limit of 1.

Limits involving algebraic operations can often be evaluated by replacing subexpressions by their limits; if the resulting expression does not determine the original limit, the expression is known as an indeterminate form.[25] In fact, when f(t) and g(t) are real-valued functions both approaching 0 (as t approaches a real number or ±∞), with f(t) > 0, the function f(t)g(t) need not approach 1; depending on f and g, the limit of f(t)g(t) can be any nonnegative real number or +∞, or it can diverge. For example, the functions below are of the form f(t)g(t) with f(t), g(t) → 0 as t → 0+, but the limits are different:

\lim _{t\to 0^{+}}{t}^{t}=1,\quad \lim _{t\to 0^{+}}\left(e^{-{\frac {1}{t^{2}}}}\right)^{t}=0,\quad \lim _{t\to 0^{+}}\left(e^{-{\frac {1}{t^{2}}}}\right)^{-t}=+\infty ,\quad \lim _{t\to 0^{+}}\left(e^{-{\frac {1}{t}}}\right)^{at}=e^{-a}.

Thus, the two-variable function xy, though continuous on the set {(x, y) : x > 0}, cannot be extended to a continuous function on any set containing (0, 0), no matter how one chooses to define 00.[26] However, under certain conditions, such as when f and g are both analytic functions and f is positive on the open interval (0, b) for some positive b, the limit approaching from the right is always 1.[27][28][29]

Complex exponents

In the complex domain, the function zw may be defined for nonzero z by choosing a branch of log z and defining zw as ew log z. This does not define 0w since there is no branch of log z defined at z = 0, let alone in a neighborhood of 0.[30][31][32]

History of differing points of view

The debate over the definition of  0^{0} has been going on at least since the early 19th century. At that time, most mathematicians agreed that  0^{0}=1, until in 1821 Cauchy[33] listed  0^{0} along with expressions like  {\frac {0}{0}} in a table of indeterminate forms. In the 1830s Libri[34][35] published an unconvincing argument for  0^{0}=1, and Möbius[36] sided with him, erroneously claiming that  \scriptstyle \lim _{t\to 0^{+}}f(t)^{g(t)}\;=\;1 whenever  \scriptstyle \lim _{t\to 0^{+}}f(t)\;=\;\lim _{t\to 0^{+}}g(t)\;=\;0. A commentator who signed his name simply as “S” provided the counterexample of  \scriptstyle (e^{-1/t})^{t}, and this quieted the debate for some time. More historical details can be found in Knuth (1992).[37]

More recent authors interpret the situation above in different ways:

  • Some argue that the best value for  0^{0} depends on context, and hence that defining it once and for all is problematic.[38] According to Benson (1999), “[t]he choice whether to define  0^{0} is based on convenience, not on correctness. If we refrain from defining  0^{0}, then certain assertions become unnecessarily awkward. […] The consensus is to use the definition 0^{0}=1, although there are textbooks that refrain from defining  0^{0}.”[39]
  • Others argue that  0^{0} should be defined as 1. Knuth (1992) contends strongly that  0^{0} “has to be 1″, drawing a distinction between the value  0^{0}, which should equal 1 as advocated by Libri, and the limiting form  0^{0} (an abbreviation for a limit of  \scriptstyle f(x)^{g(x)} where  \scriptstyle f(x),g(x)\to 0), which is necessarily an indeterminate form as listed by Cauchy: “Both Cauchy and Libri were right, but Libri and his defenders did not understand why truth was on their side.”[37]

 

或將能曉已定或未定形式答覆乎︰

Expressions that are not indeterminate forms

The expression 1/0 is not commonly regarded as an indeterminate form because there is not an infinite range of values that f/g could approach. Specifically, if f approaches 1 and g approaches 0, then f and g may be chosen so that (1) f/g approaches +∞, (2) f/g approaches −∞, or (3) the limit fails to exist. In each case the absolute value |f/g| approaches +∞, and so the quotient f/g must diverge, in the sense of the extended real numbers. (In the framework of the projectively extended real line, the limit is the unsigned infinity ∞ in all three cases.) Similarly, any expression of the form a/0, with a ≠ 0 (including a = +∞ and a = −∞), is not an indeterminate form since a quotient giving rise to such an expression will always diverge.

The expression 0∞ is not an indeterminate form. The expression 0+∞ has the limiting value 0 for the given individual limits, and the expression 0−∞ is equivalent to 1/0.

 

涉及無限、無窮，總是費思量矣☆★