每日彙整: 2017-03-04

樹莓派、樹莓派之學習、樹莓派之教育

時間序列︰生成函數《九中》

若說『成功、失敗』，或講『Yes、No』曾經困惑伯努利因何事？不為『二項式定理』太困難，只為著『二項分佈』之無窮大 \infty 的『期望值』！

Binomial distribution

In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent yes/no experiments, each of which yields success with probability p. A success/failure experiment is also called a Bernoulli experiment or Bernoulli trial; when n = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the popular binomial test of statistical significance.

The binomial distribution is frequently used to model the number of successes in a sample of size n drawn with replacement from a population of size N. If the sampling is carried out without replacement, the draws are not independent and so the resulting distribution is a hypergeometric distribution, not a binomial one. However, for N much larger than n, the binomial distribution remains a good approximation, and is widely used.

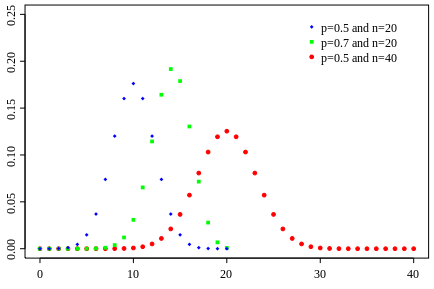
Probability mass function

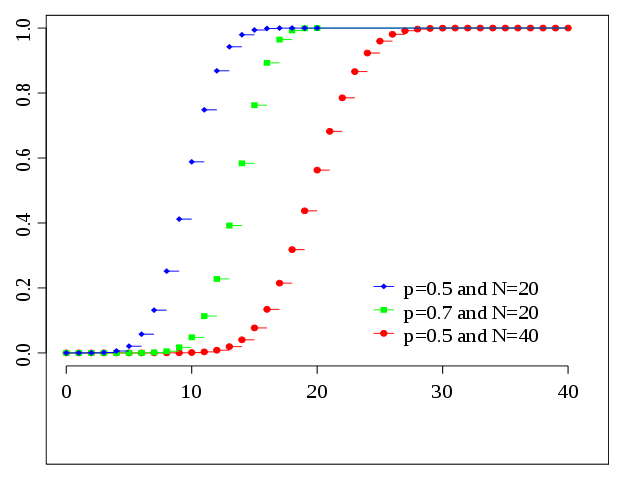
Cumulative distribution function

Specification

Probability mass function

In general, if the random variable X follows the binomial distribution with parameters n ∈ ℕ and p ∈ [0,1], we write X ~ B(n, p). The probability of getting exactly k successes in n trials is given by the probability mass function:

f(k;n,p)=\Pr(X=k)={\binom {n}{k}}p^{k}(1-p)^{n-k}

for k = 0, 1, 2, …, n, where

  {\binom {n}{k}}={\frac {n!}{k!(n-k)!}}

is the binomial coefficient, hence the name of the distribution. The formula can be understood as follows. k successes occur with probability pk and n − k failures occur with probability (1 − p)n − k. However, the k successes can occur anywhere among the n trials, and there are  {n \choose k} different ways of distributing k successes in a sequence of n trials.

In creating reference tables for binomial distribution probability, usually the table is filled in up to n/2 values. This is because for k > n/2, the probability can be calculated by its complement as

f(k,n,p)=f(n-k,n,1-p).

The probability mass function satisfies the following recurrence relation, for every  n,p:

\left\{{\begin{array}{l}p(n-k)f(k,n,p)=(k+1)(1-p)f(k+1,n,p),\\[10pt]f(0,n,p)=(1-p)^{n}\end{array}}\right\}

Looking at the expression ƒ(k, n, p) as a function of k, there is a k value that maximizes it. This k value can be found by calculating

{\frac {f(k+1,n,p)}{f(k,n,p)}}={\frac {(n-k)p}{(k+1)(1-p)}}

and comparing it to 1. There is always an integer M that satisfies

(n+1)p-1\leq M<(n+1)p.

ƒ(k, n, p) is monotone increasing for k < M and monotone decreasing for k > M, with the exception of the case where (n + 1)p is an integer. In this case, there are two values for which ƒ is maximal: (n + 1)p and (n + 1)p − 1. M is the most probable (most likely) outcome of the Bernoulli trials and is called the mode. Note that the probability of it occurring can be fairly small.

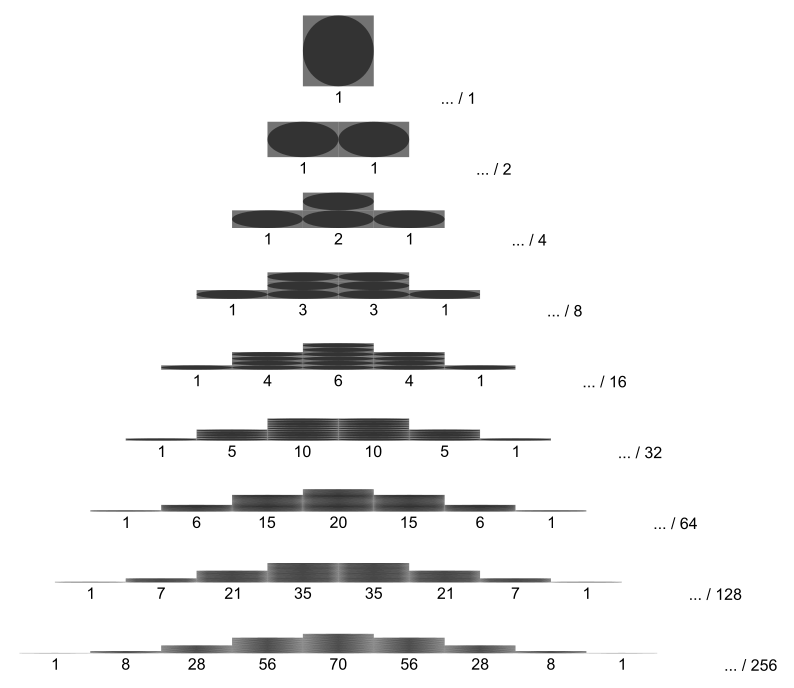
Binomial distribution for  p=0.5
with n and k as in Pascal’s triangle

The probability that a ball in a Galton box with 8 layers (n = 8) ends up in the central bin (k = 4) is  70/256.

 

莫言『機率』百分百未必然，『無窮大』尚可以分等級。且用二項分布之『生成函數』 G_B(z)

\equiv E(z^X) = \sum \limits_{k=0}^{\infty} f(k; n, p) z^k

= \sum \limits_{k=0}^{\infty} {\left( \begin{array}{ccc} n \\ k \end{array} \right)} p^k {(1-p)}^{n - k} z^k

= {(q + p z )} ^n , \ q = 1 - p

【※ 註︰當然此處取 k > n , f(k; n, p) = 0 。】

談談它的『期望值』之推導

E(X) = \lim \limits_{z \to 1^{-}} \frac{d}{d z} G_B (z) = n \cdot p 。可知無論『成功率』 p 有多小，當 n \to \infty 時，必然是趨近無窮大 \infty 矣。

事實上它的『方差』 V(X)

= \lim \limits_{z \to 1^{-}} \frac{d^2}{d^2 z} G_B (z) + \frac{d}{d z} G_B (z) - {\left( \frac{d}{d z} G_B (z) \right)}^2

= n \cdot p \cdot (1-p) 也是無窮大的哩。

 

故算術的簡單與否、形式之自動也罷，論及理解如之何哉︰

假使仔細觀察與比較用『德汝德模型』來推導『歐姆定律』，這是電子的『動量傳輸』現象 \langle \vec{p} \rangle，來自於 t 到 t + dt 間不發生『碰撞』的電子；當論述『焦耳定律』時，這又是電子的『能量移轉』現象 \langle \frac{1}{2} m v^2 \rangle，發生在 t 到 t + dt 間與『正離子』發生『碰撞』的電子。這兩個現象同時而起，各自『電場』中汲取『動量』和『能量』。為了更深入的理解，就讓我們稍微談一談『機率』與『統計』吧！

擲一個硬幣產生『正‧反』面兩種結果，這是很普通的現象，今天在『術語』上稱之為『伯努利試驗』Bernoulli trial，是說對一個只有兩種可能結果的單次『隨機試驗』，就一個『隨機變數』 X 而言，

Pr[X = 1] \ = \ p
Pr[X = 0] \ = \ 1-p = q

，此處 {Pr}_i[X_i = {\alpha}_i] = q_i 是說『隨機變數』 X_i 有 q_i 的機會取 {\alpha}_i 的值。從『期望值』的角度講

E(X) = \sum \limits_{i=1}^N {Pr}_i \cdot X_i } = 1 \cdot p + 0 \cdot (1-p) = p

，它的『標準差』 Standard Deviation 是

\delta = \sqrt{\sum \limits_{i=1}^N {Pr}_i \cdot {\left( X_i - E(X) \right)}^2} } = \sqrt{ p (1-p)}

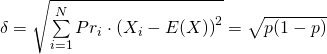
。這為什麼要叫做『伯努利試驗』的呢？一七三零年代，荷蘭出生大部分時間居住在瑞士巴塞爾的丹尼爾‧伯努利 Daniel Bernoulli 之堂兄尼古拉一世‧伯努利 Nikolaus I. Bernoulli，在致法國數學家皮耶‧黑蒙‧德蒙馬特 Pierre Rémond de Montmort 的信件中，提出了一個問題：擲 一枚硬幣，假使第一次擲出正面，你就賺了 1 元。如果第一次出現反面，那就要再擲一次，若是第二次擲的是正面，你便賺了 2 元。要是第二次擲出反面，那就得要擲第三次，假若第三次擲的是正面，你便賺 2^2 元……如此類推，也就是說你可能擲一次遊戲就結束了，也許會反覆擲個沒完沒了。問題是，你最多肯付多少錢來玩這個遊戲的呢？假使從『期望值』來考量，這個遊戲的期望值是『無限大』

E=\frac{1}{2}\cdot 1+\frac{1}{4}\cdot 2 + \frac{1}{8}\cdot 4 + \frac{1}{16}\cdot 8 + \cdots
=\frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \cdots
=\sum \limits_{k=1}^\infty {1 \over 2}=\infty

，然而即使你願意付出『無限的金錢』去參與這個遊戲。不過，你卻可能只賺到 1 元，或 2 元，或 4 元……等等，只怕不可能賺到無限的金錢。那你又為什麼肯付出巨額的金錢加入遊戲的呢？

其後丹尼爾‧白努利於一七三八年寫了一篇論文『風險度量的新理論之討論』考慮了一個對等的遊戲，不斷的擲同一枚硬幣，直到獲得正面為止，如果你擲了 N 次才最終得到正面，你將獲得 2^{N - 1} 元。即使參與玩這個遊戲的花費是『天價』，假使我們考慮到這個遊戲的『期望收益』是無窮大，我們就應該參加。這就是史稱的『聖彼得堡悖論』。白努利提出了一個理論來解釋這個悖論，他得到了一條原理，『財富越多人越滿足，然而隨著財富的累積，滿足程度的增加率卻不斷下降』。這或許可以說是古典的『邊際效用遞減』版本，就像『白手起家』和其後之『錦上添花』，對一個人的『效用』之『滿足』是完全不同的一樣。他這麼講︰

【邊際效用遞減原理】：一個人對於財富的佔有多多益善，就是說『效用函數』一階導數大於零；隨著財富的增加，滿足程度的增加速度不斷下降，正因為『效用函數』二階導數小於零。

【最大效用原理】：在『風險』和『不確定』的條件下，一個人行為的『決策準則』是為了獲得最大『期望效用』值而不是最大『期望金額』值。

作者不知『理性』是否該『相信』期望值，或者『感性』果就會『追求』效用量，彷彿『天下』到底是『患寡』還是『患不均』的呢？？

事實上一個『發生』或『不發生』，『存在』也許『不存在』，是『成功』還是『失敗』的『可‧不可』 Yes or No 的『事件機率』能夠表達的『現象界』不勝枚舉，就像『德汝德模型』中『電子』之『碰撞』與『不碰撞』也是一樣的。假使我們將『伯努利試驗』推廣到 n 次中有 k 次的『成功率』，我們就得到了數學上所謂的『二項分佈』

\Pr(X = k) = {n\choose k}p^k(1-p)^{n-k} = {n\choose k}p^k(q)^{n-k}

，此處 {n\choose k} = \frac{n!}{k!(n-k)!} 是 n 中取 k 之『組合數』。假使 n 很大，且機率 p 很小，這個『二項分佈』可以『近似』如下︰

如果 \lambda = n p 是有限大小的『適度量』，回顧指數函數 e 的定義之一是

\lim \limits_{n\to\infty}\left(1-{\lambda \over n}\right)^n=e^{-\lambda}

依據二項分佈的定義：

P(X=k)={n \choose k} p^k (1-p)^{n-k}

如果假設 p = \lambda/n，當 n 趨於無窮時， P 的極限可以如此計算

\lim \limits_{n\to\infty} P(X=k)&=\lim \limits_{n\to\infty}{n \choose k} p^k (1-p)^{n-k}

=\lim \limits_{n\to\infty}{n! \over (n-k)!k!} \left({\lambda \over n}\right)^k \left(1-{\lambda\over n}\right)^{n-k}

=\lim \limits_{n\to\infty} \underbrace{\left[\frac{n!}{n^k\left(n-k\right)!}\right]}_F \left(\frac{\lambda^k}{k!}\right) \underbrace{\left(1-\frac{\lambda}{n}\right)^n}_{\to\exp\left(-\lambda\right)} \underbrace{\left(1-\frac{\lambda}{n}\right)^{-k}}_{\to 1}

= \lim \limits_{n\to\infty} \underbrace{\left[ \left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right) \ldots \left(1-\frac{k-1}{n}\right) \right]}_{\to 1} \left(\frac{\lambda^k}{k!}\right) \underbrace{\left(1-\frac{\lambda}{n}\right)^n}_{\to\exp\left(-\lambda\right)} \underbrace{\left(1-\frac{\lambda}{n}\right)^{-k}}_{\to 1}

= \left(\frac{\lambda^k}{k!}\right)\exp\left(-\lambda\right) 。

─── 摘自《【Sonic π】電路學之補充《一》》