孤虛者言︰
物有無者,非真假也。苟日新,日日新,又日新。真假者,物之論也。論也者,當或不當而已矣。故世有孤虛者,言有孤虛論。孤虛何謂也?甲乙孤虛,言不得全真也,索其孤其虛而已矣。天地孤虛 ,去其上下也,善惡孤虛,何得善惡並真乎?是故孤虛論全矣!
其法曰︰物物孤虛,言物之非也;孤虛之孤虛,此孤虛 之非也。使甲與乙並,此甲乙孤虛之非也,強使之或,乃非甲非乙之孤虛也。若云由此及彼,雖言之鑿鑿,若非彼與此之孤虛,无能以斷疑是也 !!
假使依據孤虛 ── Sheffer 豎線 ──所說則︰
非 ︰
且
︰
或
︰
若 則
︰
─ 摘自《M♪o 之學習筆記本《子》開關︰【黑水智】數位之源》
並非邏輯太困難,所以難以掌握。有時只是符號陌生,講法不通俗使然。思維常因習以為常,故有定勢,以至常會忽略某些細節未能貫通。兩個無窮級數
![]() 、
、 ![]()
的乘積
![]()
雖說是從有限級數乘法展開推廣而來。假使將之表述成
柯西乘積
在數學上,以法國數學家奧古斯丁·路易·柯西命名的柯西乘積,是指兩組數列 的離散卷積。
級數
一個特別重要的例子是考慮兩個嚴格的形式級數(不需要收斂) :
-
- 這裡
- 這裡
「形式」是指我們對級數運算時不考慮是否收斂,參見形式冪級數 。
人們希望,通過對兩組級數做實際卷積的有限和的類推,得到無窮級數
等於如下乘積:
就如同兩個數列的和是有限範圍一樣做乘法。
在充分良態(well-behaved)的情況下,上述式子成立。而更重要的一點,儘管這兩個無窮級數可能不收斂,它們的柯西乘積仍可能存在。
務須注意『卷積』的意義。否則恐有數學語言『誤用』之嫌。
Definitions
The Cauchy product may apply to infinite series[1][2][3][4][5][6][7][8][9][10][11] or power series.[12][13] When people apply it to finite sequences[14] or finite series, it is by abuse of language: they actually refer to discrete convolution.
Convergence issues are discussed in the next section.
※
Discrete convolution
For complex-valued functions f, g defined on the set Z of integers, the discrete convolution of f and g is given by:[9]
The convolution of two finite sequences is defined by extending the sequences to finitely supported functions on the set of integers. When the sequences are the coefficients of two polynomials, then the coefficients of the ordinary product of the two polynomials are the convolution of the original two sequences. This is known as the Cauchy product of the coefficients of the sequences.
Thus when g has finite support in the set (representing, for instance, a finite impulse response), a finite summation may be used:[10]
───
實因有限級數的乘法
![]()
既無規定的『次序』,所謂 ![]() 也不過『指標』罷了,叫什麼名字並不重要。這可與有限序列捲積之內涵根本不同。
也不過『指標』罷了,叫什麼名字並不重要。這可與有限序列捲積之內涵根本不同。
因此假借『冪級數』想像比較直覺的吧。
Cauchy product of two infinite series
Let and
be two infinite series with complex terms. The Cauchy product of these two infinite series is defined by a discrete convolution as follows:
-
where
.
Cauchy product of two power series
Consider the following two power series
-
and
with complex coefficients and
. The Cauchy product of these two power series is defined by a discrete convolution as follows:
-
where
.
如是,柯西乘積的意義可以彰顯
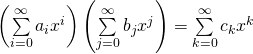 ,
,
此指『等冪』 ![]() 之
之 ![]() 的係數
的係數 ![]() 可由
可由 ![]() 貢獻
貢獻 ![]() ,
,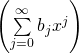 貢獻
貢獻 ![]() 得出︰
得出︰
![]() 。
。
當然也可以記作 ![]() ,將之改寫成︰
,將之改寫成︰
![]() 哩。
哩。
反演 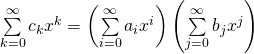 時,小心『指標算術』勒。
時,小心『指標算術』勒。
那麼白努利多項式
![]()
之生成函數可以推導如下矣︰
![]()
![]()
![]()
![]()
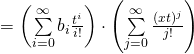
![]()






![{\displaystyle {\begin{aligned}(f*g)[n]&\ {\stackrel {\mathrm {def} }{=}}\ \sum _{m=-\infty }^{\infty }f[m]\,g[n-m]\\&=\sum _{m=-\infty }^{\infty }f[n-m]\,g[m].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de7e5972470c44c5b5788bf3372578b5f2363d49)
![(f*g)[n]=\sum _{m=-M}^{M}f[n-m]g[m].](https://wikimedia.org/api/rest_v1/media/math/render/svg/fddacde29cbcb3c6fca263493335c31a4d2ebce2)
