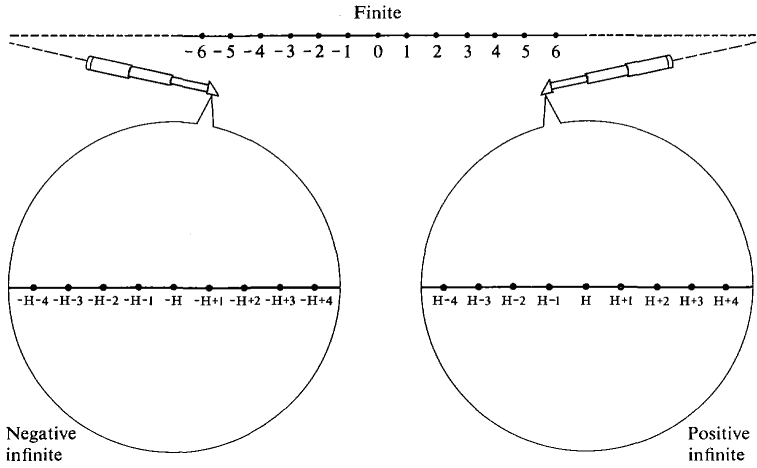
無限大 ![]() 巨量也,比任何給定的正量都大。它的倒數
巨量也,比任何給定的正量都大。它的倒數 ![]() 是無窮小也,故比任何給定的正量都小。如果無限大有等級,當然無窮小也有等級的了。過去作者曾經寫過一系列文本《【Sonic π】電路學之補充《四》無窮小算術‧上》介紹 Robinson 先生之直觀微積分︰
是無窮小也,故比任何給定的正量都小。如果無限大有等級,當然無窮小也有等級的了。過去作者曾經寫過一系列文本《【Sonic π】電路學之補充《四》無窮小算術‧上》介紹 Robinson 先生之直觀微積分︰
一九六零年,德國數學家『亞伯拉罕‧魯濱遜』 Abraham Robinson 將『萊布尼茲』的微分直觀落實。 用嚴謹的方法來定義和運算實數的『無窮小』與『無限大』,這就是數學史上著名的『非標準微積分』Non-standard calculus ,可說是『非標準分析』non-standard analysis 之父。
就像『複數』 ![]() 是『實數系』
是『實數系』 ![]() 的『擴張』一樣,他將『實數系』增入了『無窮小』 infinitesimals 元素
的『擴張』一樣,他將『實數系』增入了『無窮小』 infinitesimals 元素 ![]() ,魯濱遜創造出『超實數』 hyperreals
,魯濱遜創造出『超實數』 hyperreals ![]() ,形成了『超實數系』
,形成了『超實數系』 ![]() 。那這個『無窮小』是什麼樣的『數』呢?對於『正無窮小』來說,任何給定的『正數』都比要它大,就『負無窮小』來講,它大於任何給定的『負數』。 『零』也就自然的被看成『實數系』裡的『無窮小』的了。假使我們說兩個超實數
。那這個『無窮小』是什麼樣的『數』呢?對於『正無窮小』來說,任何給定的『正數』都比要它大,就『負無窮小』來講,它大於任何給定的『負數』。 『零』也就自然的被看成『實數系』裡的『無窮小』的了。假使我們說兩個超實數 ![]() 是『無限的鄰近』 indefinitly close,記作
是『無限的鄰近』 indefinitly close,記作 ![]() 是指
是指 ![]() 是個『無窮小』量。在這個觀點下,『無窮小』量不滿足『實數』的『阿基米德性質』。也就是說,對於任意給定的
是個『無窮小』量。在這個觀點下,『無窮小』量不滿足『實數』的『阿基米德性質』。也就是說,對於任意給定的 ![]() 來講,
來講, ![]() 為『無窮小』量;而
為『無窮小』量;而 ![]() 是『無限大』量。然而在『系統』與『自然』的『擴張』下,『超實數』的『算術』符合所有一般『代數法則』。
是『無限大』量。然而在『系統』與『自然』的『擴張』下,『超實數』的『算術』符合所有一般『代數法則』。
有人把『超實數』想像成『數原子』,一個環繞著『無窮小』數的『實數』。就像『複數』有『實部』 ![]() 與『虛部』
與『虛部』 ![]() 取值『運算』一樣,『超實數』也有一個取值『運算』叫做『標準部份函數』Standard part function
取值『運算』一樣,『超實數』也有一個取值『運算』叫做『標準部份函數』Standard part function
![]()
![]()
。 如此一個『函數』 ![]() 在
在 ![]() 是『連續的』就可以表示成『如果
是『連續的』就可以表示成『如果 ![]() ,可以得到
,可以得到 ![]() 』。
』。
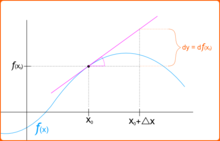
假使 ![]() ,那麼
,那麼 ![]() 的『斜率』就可以這麼計算
的『斜率』就可以這麼計算
![]()
![]()
。 彷彿在用著可以調整『放大倍率』的『顯微鏡』逐步『觀入』 zoom in 一個『函數』,隨著『解析度』的提高,函數之『曲率』逐漸減小,越來越『逼近』一條『直線』── 某點的切線 ── 的啊!!
同樣的『積分』就像是『里程表』的『累計』一樣,可以用
![]()
來表示的呀!!
─── 摘自《【Sonic π】電路學之補充《四》無窮小算術‧中》
希望讀者能夠深入理解實數的基本性質,以及由之而來的各種抽象論證︰
最小上界性質
Let S be a non-empty set of real numbers:
A real number x is called an upper bound for S if x ≥ s for all s ∈ S. A real number x is the least upper bound (or supremum) for S if x is an upper bound for S and x ≤ y for every upper bound y of S.
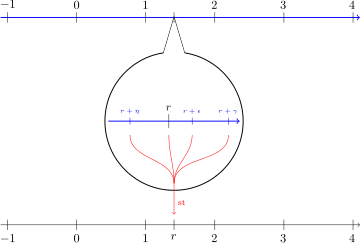
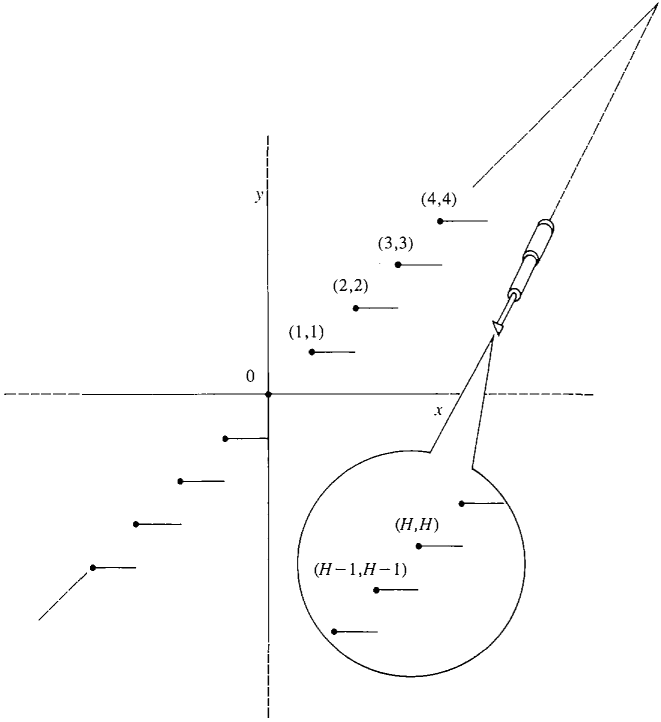
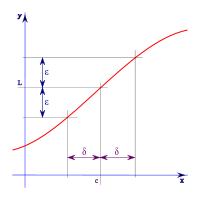
從『疊套區間』的觀點來看,一個『超實數』 ![]() 就可以表達成
就可以表達成 ![]() ,而且說
,而且說 ![]() ,由於它只有『唯一的』一個元素,所以被稱作『單子集合』 singleton set。假使我們思考一個『單調上升有上界』
,由於它只有『唯一的』一個元素,所以被稱作『單子集合』 singleton set。假使我們思考一個『單調上升有上界』 ![]() 的『序列』,會發現它一定有『最小上界』。假設
的『序列』,會發現它一定有『最小上界』。假設 ![]() 是一個『巨量』,那麼
是一個『巨量』,那麼 ![]()
。這就是『實數』的『基本性質』,任何一有極限的『序列』收斂於一個『唯一』的『實數』,一般稱之為『實數』的『完備性』 completeness,由於我們是站在『超實數』的立場,選擇了『疊套區間』的觀點,加之以『無窮小』量不滿足『實數』的『阿基米德性質』,所以這個『實數』的『完備性』只是從『疊套區間』確定了一個『單子集合』 推導的結論。對比著來看,這一個『有理數』序列 ![]() 的『極限』
的『極限』 ![]() ,它可從求解
,它可從求解 ![]() 得到,然而它並不是『有理數』,所以說『有理數』不具有『完備性』 。那麼對一個『非空有上界』的『集合』
得到,然而它並不是『有理數』,所以說『有理數』不具有『完備性』 。那麼對一個『非空有上界』的『集合』 ![]() ,也可以用『二分逼近法』論證如下︰
,也可以用『二分逼近法』論證如下︰
由 於 ![]() 有上界,就說是
有上界,就說是 ![]() 吧,因為
吧,因為 ![]() 不是空集合,一定有一個元素
不是空集合,一定有一個元素 ![]() 不是它的上界。這兩個序列可以遞迴的如此定義,計算
不是它的上界。這兩個序列可以遞迴的如此定義,計算 ![]() ,如果它是
,如果它是 ![]() 的上界,那麼
的上界,那麼 ![]() ,否則
,否則 ![]() 中必有一個元素
中必有一個元素 ![]() ,而且
,而且 ![]() ,此時選擇
,此時選擇 ![]() ,如此
,如此 ![]() 而且
而且 ![]() ,所以一定存在一個
,所以一定存在一個 ![]() ,此為
,此為 ![]() 之最小上界。
之最小上界。
同理 ![]() 的補集
的補集 ![]() 就會有『下界』,而且會有『最大下界』。因此我們將一個有『上界』與『下界』的集合,簡稱之為『有界集合』。
就會有『下界』,而且會有『最大下界』。因此我們將一個有『上界』與『下界』的集合,簡稱之為『有界集合』。
『實數集合』的『最小上界』性質,可以用來證明『實數分析』上的多條定理,在此僅列舉幾條『常用的』︰
【波爾查諾‧魏爾斯特拉斯定理】 任一實數 ![]() 中的有界序列
中的有界序列 ![]() 至少包含一個收斂的子序列。
至少包含一個收斂的子序列。
讓我們從 ![]() 中選擇元素,建構一個『峰值集合』
中選擇元素,建構一個『峰值集合』 ![]() ,假使
,假使 ![]() 的元素是『有限的』,就可將之大小『排序』,建立序列
的元素是『有限的』,就可將之大小『排序』,建立序列 ![]() 。如果
。如果 ![]() 的元素是『無限的』,我們依然可以用『下標』
的元素是『無限的』,我們依然可以用『下標』 ![]() 遞增的方式從
遞增的方式從 ![]() 中選擇建立『序列』
中選擇建立『序列』![]() ,這兩者都是『單調上升有界』的序列,所以必然會有『最小上界』。
,這兩者都是『單調上升有界』的序列,所以必然會有『最小上界』。
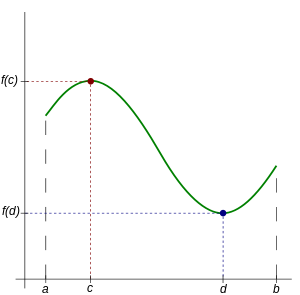
【極值定理】如果實數函數 ![]() 是閉區間
是閉區間 ![]() 上的『連續函數』,那麼它在其間一定會有『最大值』和『最小值』。也就是說,存在
上的『連續函數』,那麼它在其間一定會有『最大值』和『最小值』。也就是說,存在 ![]() 兩個『極值』使得
兩個『極值』使得 ![]() 。
。
假設函數 ![]() 沒有上界。那麼,根據實數的『阿基米德性質』,對於每一個自然數
沒有上界。那麼,根據實數的『阿基米德性質』,對於每一個自然數 ![]() ,都可以有一個
,都可以有一個 ![]() ,使得
,使得 ![]() ,這就構成了一個『有界的序列』
,這就構成了一個『有界的序列』 ![]() ,然而依據『波爾查諾‧魏爾斯特拉斯定理』,這個
,然而依據『波爾查諾‧魏爾斯特拉斯定理』,這個 ![]() 序列至少會有一個收斂的『子序列』
序列至少會有一個收斂的『子序列』 ![]() ,就稱它的極限值是
,就稱它的極限值是 ![]() ,此處
,此處 ![]() 是『巨量』。因為
是『巨量』。因為 ![]() 在閉區間
在閉區間 ![]() 中『連續』,於是
中『連續』,於是 ![]() 也是『有限量』,然而依據『假設』
也是『有限量』,然而依據『假設』 ![]() ,故而矛盾,所以實數函數
,故而矛盾,所以實數函數 ![]() 是有『上界的』。只需考慮
是有『上界的』。只需考慮 ![]() ,從它有『上界』,就可以得到
,從它有『上界』,就可以得到 ![]() 一定有『下界』的吧!也就是說一個實數的『連續』函數,因其『連續性』將一個『定義域』的『閉區間』映射到『對應域』的『閉區間』,所以也必將『無窮小』閉區間
一定有『下界』的吧!也就是說一個實數的『連續』函數,因其『連續性』將一個『定義域』的『閉區間』映射到『對應域』的『閉區間』,所以也必將『無窮小』閉區間 ![]() 映射到『無窮小』閉區間
映射到『無窮小』閉區間 ![]() 的啊!!事實上,『無窮小』閉區間
的啊!!事實上,『無窮小』閉區間 ![]() 可以看成
可以看成 ![]() 點的『鄰域』,難道說所謂的函數
點的『鄰域』,難道說所謂的函數 ![]() 在
在 ![]() 點『連續』,
點『連續』,![]() 可能不在這個『無窮小鄰域』裡無限的『逼近』
可能不在這個『無窮小鄰域』裡無限的『逼近』 ![]() 的嗎??
的嗎??
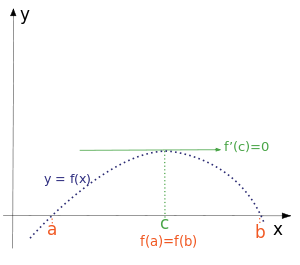
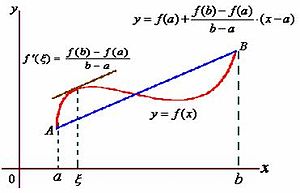
【羅爾定理】如果一個實數函數 ![]() 滿足
滿足
在閉區間 ![]() 上『連續』;
上『連續』;
在開區間 ![]() 內『可微分』;
內『可微分』;
在區間端點處的函數值相等,即 ![]() ,
,
那麼在開區間 ![]() 之內至少有一點
之內至少有一點 ![]() ,使得
,使得 ![]() 。
。
根據『極值定理』 ,實數函數 ![]() 在閉區間
在閉區間 ![]() 裡有『極大值』
裡有『極大值』 ![]() 和『極小值』
和『極小值』 ![]() ,如果它們都同時發生在『端點』
,如果它們都同時發生在『端點』 ![]() 或
或 ![]() 處,由於
處,由於 ![]() 而且
而且 ![]() ,因此
,因此 ![]() 是一個『常數函數』,所以
是一個『常數函數』,所以 ![]() 。除此之外『極大值』
。除此之外『極大值』 ![]() 或『極小值』
或『極小值』 ![]() 之一只能發生在開區間
之一只能發生在開區間 ![]() 之內,假設於
之內,假設於 ![]() 處取得了『極大值』
處取得了『極大值』 ![]() ,因此
,因此 ![]() ,而且
,而且 ![]() ,由於
,由於 ![]() ,
, ![]() ,同時
,同時 ![]() ,
, ![]() ,再由於函數
,再由於函數 ![]() 在
在 ![]() 處『可微分』,所以
處『可微分』,所以 ![]() 。同理也可以證明
。同理也可以證明 ![]() 有『極小值』
有『極小值』 ![]() 時,
時,![]() 。也可以講『羅爾定理』將『連續性』、『可微分性』與『極值』聯繫了起來,在此強調那個『可微分』的條件是『必要的』。舉個例子說,函數
。也可以講『羅爾定理』將『連續性』、『可微分性』與『極值』聯繫了起來,在此強調那個『可微分』的條件是『必要的』。舉個例子說,函數 ![]() 在
在 ![]() 處有『極小值』,考慮它的『無窮小鄰域』
處有『極小值』,考慮它的『無窮小鄰域』 ![]() ,右方逼近的『導數』是
,右方逼近的『導數』是 ![]() ,然而左方逼近的『導數』是
,然而左方逼近的『導數』是 ![]() ,因此這個函數於『此點』不可微分,此時當然『羅爾定理』也就不適用的了!!
,因此這個函數於『此點』不可微分,此時當然『羅爾定理』也就不適用的了!!
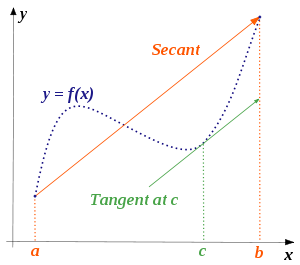
【均值定理】一個實數函數 ![]() 在閉區間
在閉區間 ![]() 裡『連續』且於開區間
裡『連續』且於開區間 ![]() 中『可微分』,那麼一定存在一點
中『可微分』,那麼一定存在一點 ![]() 使得此點的『切線斜率』等於兩端點間的『割線斜率』,即
使得此點的『切線斜率』等於兩端點間的『割線斜率』,即 ![]() 。
。
假使藉著 ![]() 定義一個函數
定義一個函數 ![]() ,這個
,這個 ![]() 函數在閉區間
函數在閉區間 ![]() 裡『連續』且於開區間
裡『連續』且於開區間 ![]() 中『可微分』,同時
中『可微分』,同時 ![]() ,於是依據『羅爾定理』一定有一點
,於是依據『羅爾定理』一定有一點 ![]() 使得
使得 ![]() ,所以
,所以 ![]() 。
。
─── 摘自《【Sonic π】電路學之補充《四》無窮小算術‧下》
通熟者或只需告之定義 ![]() ,知道
,知道 ![]() ,就可以從『羅爾定理』證明
,就可以從『羅爾定理』證明
柯西均值定理
柯西均值定理,也叫拓展均值定理,是均值定理的一般形式。它敘述為:如果函數f和g都在閉區間[a,b]上連續,且在開區間(a, b)上可導,那麼存在某個c ∈ (a,b),使得
當然,如果g(a) ≠ g(b)並且g′(c) ≠ 0,這等價於:
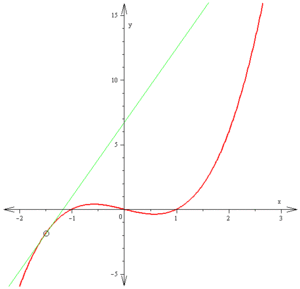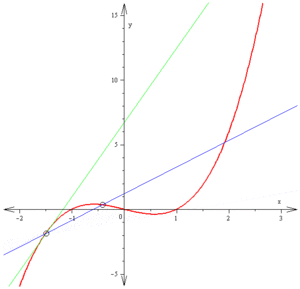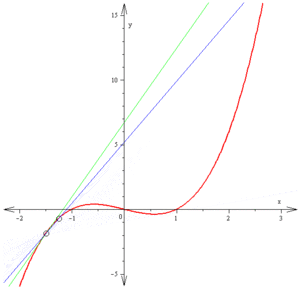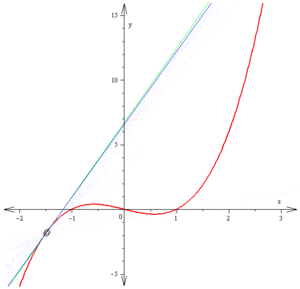
在幾何上,這表示曲線
的圖像存在平行於由(f(a),g(a))和(f(b),g(b))確定的直線的切線。但柯西定理不能表明在任何情況下不同的兩點(f(a),g(a))和(f(b),g(b))都存在切線,因為可能存在一些c值使f′(c) = g′(c) = 0,換句話說取某個值時位於曲線的駐點;在這些點似乎曲線根本沒有切線。下面是這種情形的一個例子
在區間[−1,1]上,曲線由(−1,0)到(1,0),卻並無一個水平切線;然而它有一個駐點(實際上是一個尖點)在t = 0時。
柯西均值定理可以用來證明羅必達法則. (拉格朗日)均值定理是柯西均值定理當g(t) = t時的特殊情況。
的吧。如是者可否藉著『柯西均值定理』證明
羅必達法則
羅必達法則(l’Hôpital’s rule)是利用導數來計算具有不定型的極限的方法。這法則是由瑞士數學家約翰·伯努利(Johann Bernoulli)所發現的,因此也被叫作伯努利法則(Bernoulli’s rule)。
敘述
羅畢達法則可以求出特定函數趨近於某數的極限值。令 (擴展實數),兩函數
在以
為端點的開區間可微,
,並且
。
如果 或
其中一者成立,則稱欲求的極限
為未定式。
此時羅必達法則表明:
。
對於不符合上述分數形式的未定式,可以透過運算轉為分數形式,再以本法則求其值。以下列出數例:
| 欲求的極限 | 條件 | 轉換為分數形式的方法 |
|---|---|---|
| (1)
|
|
|
| (2) |
|
|
| (3) |
|
|
| (4) |
|
|
注意
不能在數列形式下直接用羅必達法則,因為對於離散變量是無法求導數的。但此時有形式類近的斯托爾茲-切薩羅定理 (Stolz-Cesàro theorem)作為替代。
乎??進而論證
斯托爾茲-切薩羅定理
斯托爾茲-切薩羅定理(英語:Stolz–Cesàro theorem)是數學分析學中的一個用於證明數列收歛的定理。該定理以奧地利人奧托·施托爾茨和義大利人恩納斯托·切薩羅命名。
內容
設 和
為兩個實數數列。若
為嚴格單調的無界正數數列,且有窮極限
存在,則
也存在且等於ℓ。
用法說明
該定理雖然主要被用來處理數列不定型極限[1][2],但該定理在沒有 這一限制條件時也是成立的[2]。雖然該定理通常是以分母
為正數數列的情形加以敘述的,但注意到該定理對分子
的正負沒有限制,所以原則上把對數列
的限制條件替換為「嚴格單調遞減且趨於負無窮大」也是沒有問題的。
與洛必達法則的疊代用法類似,在嘗試應用斯托爾茲-切薩羅定理考察數列的極限時,如果發現兩個數列差分的商仍然是不定型,可以嘗試再使用1次該定理,考察其2階差分之商的極限。[2]
應當注意,當 
必定也不存在。換句話說,確實有「有窮極限
存在,但有窮極限

直觀解釋
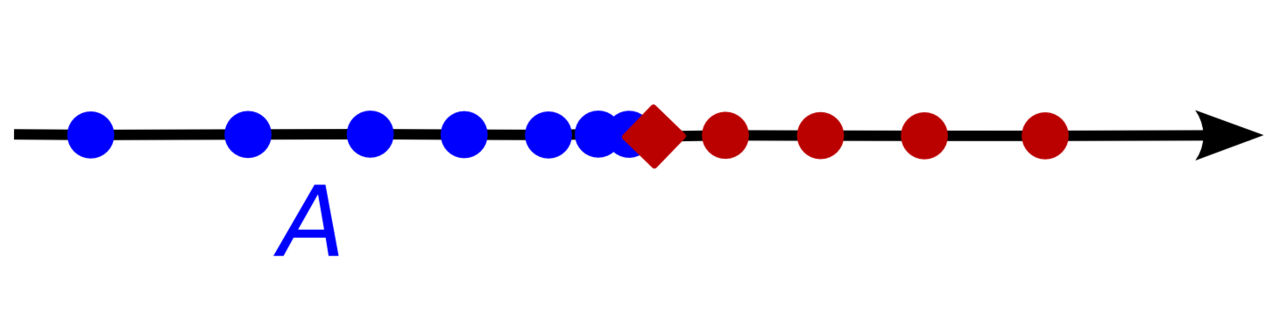
利用與折線斜率的類比,該定理具有直觀的幾何意義。[2]
耶!!




![\begin{array}{ccc}[a,b]&\longrightarrow&\mathbb{R}^2\\t&\mapsto&\bigl(f(t),g(t)\bigr),\end{array}](https://wikimedia.org/api/rest_v1/media/math/render/svg/235d2bf7fea49e46f129baf3711f9a22140dd970)