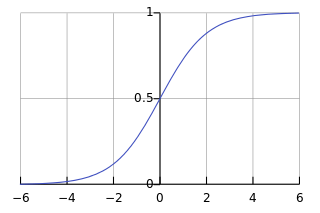
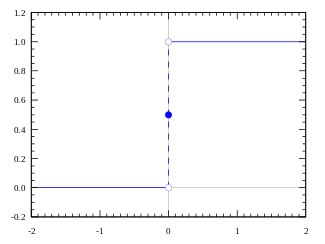
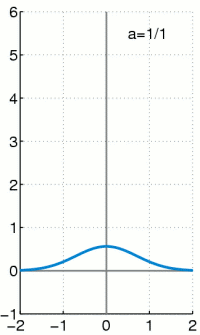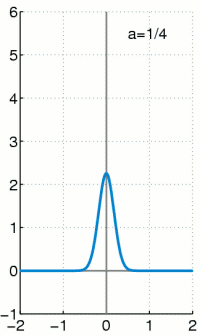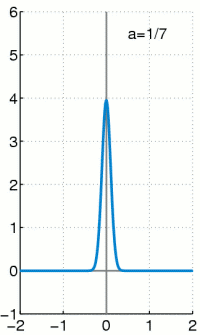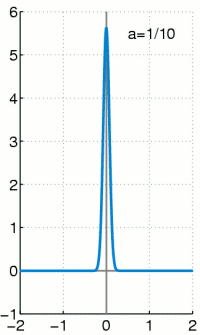
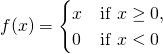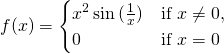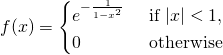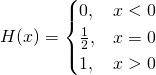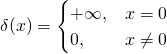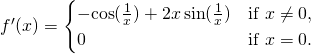此處 Michael Nielsen 先生談起『理論』上可行的方法,『實務』上可能會不管用!!??
People have investigated many variations of gradient descent, including variations that more closely mimic a real physical ball. These ball-mimicking variations have some advantages, but also have a major disadvantage: it turns out to be necessary to compute second partial derivatives of ![]() , and this can be quite costly. To see why it’s costly, suppose we want to compute all the second partial derivatives
, and this can be quite costly. To see why it’s costly, suppose we want to compute all the second partial derivatives ![]() . If there are a million such
. If there are a million such ![]() variables then we’d need to compute something like a trillion (i.e., a million squared) second partial derivatives*
variables then we’d need to compute something like a trillion (i.e., a million squared) second partial derivatives*
*Actually, more like half a trillion, since ![]() . Still, you get the point.!
. Still, you get the point.!
That’s going to be computationally costly. With that said, there are tricks for avoiding this kind of problem, and finding alternatives to gradient descent is an active area of investigation. But in this book we’ll use gradient descent (and variations) as our main approach to learning in neural networks.
How can we apply gradient descent to learn in a neural network? The idea is to use gradient descent to find the weights wk and biases bl which minimize the cost in Equation (6). To see how this works, let’s restate the gradient descent update rule, with the weights and biases replacing the variables ![]() . In other words, our “position” now has components
. In other words, our “position” now has components ![]() and
and ![]() , and the gradient vector
, and the gradient vector ![]() has corresponding components
has corresponding components ![]() and
and ![]() . Writing out the gradient descent update rule in terms of components, we have
. Writing out the gradient descent update rule in terms of components, we have
By repeatedly applying this update rule we can “roll down the hill”, and hopefully find a minimum of the cost function. In other words, this is a rule which can be used to learn in a neural network.
There are a number of challenges in applying the gradient descent rule. We’ll look into those in depth in later chapters. But for now I just want to mention one problem. To understand what the problem is, let’s look back at the quadratic cost in Equation (6). Notice that this cost function has the form ![]() , that is, it’s an average over costs
, that is, it’s an average over costs ![]() for individual training examples. In practice, to compute the gradient
for individual training examples. In practice, to compute the gradient ![]() we need to compute the gradients
we need to compute the gradients ![]() separately for each training input,
separately for each training input, ![]() , and then average them,
, and then average them, ![]() . Unfortunately, when the number of training inputs is very large this can take a long time, and learning thus occurs slowly.
. Unfortunately, when the number of training inputs is very large this can take a long time, and learning thus occurs slowly.
An idea called stochastic gradient descent can be used to speed up learning. The idea is to estimate the gradient ![]() by computing
by computing ![]() for a small sample of randomly chosen training inputs. By averaging over this small sample it turns out that we can quickly get a good estimate of the true gradient
for a small sample of randomly chosen training inputs. By averaging over this small sample it turns out that we can quickly get a good estimate of the true gradient ![]() , and this helps speed up gradient descent, and thus learning.
, and this helps speed up gradient descent, and thus learning.
………
什麼是『隨機』呢?維基百科詞條這麼說︰
Stochastic
The term stochastic occurs in a wide variety of professional or academic fields to describe events or systems that are unpredictable due to the influence of a random variable. The word “stochastic” comes from the Greek word στόχος (stokhos, “aim”).
Researchers refer to physical systems in which they are uncertain about the values of parameters, measurements, expected input and disturbances as “stochastic systems”. In probability theory, a purely stochastic system is one whose state is randomly determined, having a random probability distribution or pattern that may be analyzed statistically but may not be predicted precisely. In this regard, it can be classified as non-deterministic (i.e., “random”) so that the subsequent state of the system is determined probabilistically. Any system or process that must be analyzed using probability theory is stochastic at least in part.[1][2] Stochastic systems and processes play a fundamental role in mathematical models of phenomena in many fields of science, engineering, finance and economics.
───
或可嘗試進一步了解︰
Stochastic gradient descent
Stochastic gradient descent (often shortened in SGD) is a stochastic approximation of the gradient descent optimization method for minimizing an objective function that is written as a sum of differentiable functions.
Iterative method
In stochastic (or “on-line”) gradient descent, the true gradient of 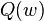 is approximated by a gradient at a single example:
is approximated by a gradient at a single example:
As the algorithm sweeps through the training set, it performs the above update for each training example. Several passes can be made over the training set until the algorithm converges. If this is done, the data can be shuffled for each pass to prevent cycles. Typical implementations may use an adaptive learning rate so that the algorithm converges.
In pseudocode, stochastic gradient descent can be presented as follows:
- Choose an initial vector of parameters
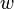 and learning rate
and learning rate 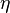 .
. - Repeat until an approximate minimum is obtained:
- Randomly shuffle examples in the training set.
- For
 , do:
, do:
A compromise between computing the true gradient and the gradient at a single example, is to compute the gradient against more than one training example (called a “mini-batch”) at each step. This can perform significantly better than true stochastic gradient descent because the code can make use of vectorization libraries rather than computing each step separately. It may also result in smoother convergence, as the gradient computed at each step uses more training examples.
The convergence of stochastic gradient descent has been analyzed using the theories of convex minimization and of stochastic approximation. Briefly, when the learning rates 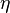 decrease with an appropriate rate, and subject to relatively mild assumptions, stochastic gradient descent converges almost surely to a global minimum when the objective function is convex or pseudoconvex, and otherwise converges almost surely to a local minimum.[3] [4] This is in fact a consequence of the Robbins-Siegmund theorem.[5]
decrease with an appropriate rate, and subject to relatively mild assumptions, stochastic gradient descent converges almost surely to a global minimum when the objective function is convex or pseudoconvex, and otherwise converges almost surely to a local minimum.[3] [4] This is in fact a consequence of the Robbins-Siegmund theorem.[5]
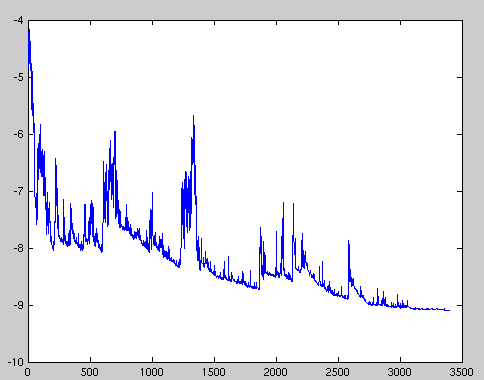
Fluctuations in the total objective function as gradient steps with respect to mini-batches are taken.
───
或可藉『統計力學』揣想它之『合理性』可能有根源耶??!!
假使我們思考這樣的一個『問題』︰
一個由大量粒子構成的『物理系統』,這些粒子具有某一個『物理過程』描述的『隨機變量』 ![]() ,那麼在
,那麼在 ![]() 時刻,這個『隨機變量』的『大數平均值』
時刻,這個『隨機變量』的『大數平均值』
![]()
,是這個『物理系統』由大量粒子表現的『瞬時圖像』,也就是『統計力學』上所說的『系綜平均』ensemble average 值。再從一個『典型粒子』的『隨機運動』上講,這個『隨機變量』 ![]() 會在不同時刻隨機的取值,因此就可以得到此一個『典型粒子』之『隨機變量』的『時間平均值』
會在不同時刻隨機的取值,因此就可以得到此一個『典型粒子』之『隨機變量』的『時間平均值』
![]()
,這說明了此一『典型粒子』在『物理系統』中的『歷時現象』 ,那麼此兩種平均值,它們的大小是一樣的嗎??
在『德汝德模型』中我們已經知道 ![]() 是一個『電子』於
是一個『電子』於 ![]() 時距裡不發生碰撞的機率。這樣
時距裡不發生碰撞的機率。這樣 ![]() 的意思就是,在
的意思就是,在 ![]() 到
到 ![]() 的時間點發生碰撞的機率。參考指數函數
的時間點發生碰撞的機率。參考指數函數 ![]() 的『泰勒展開式』
的『泰勒展開式』
![]()
,如此
![]()
![]()
,這倒過來說明了為什麼在『德汝德模型』中,發生碰撞的機率是 ![]() ,於是一個有
,於是一個有 ![]() 個『自由電子』的導體,在
個『自由電子』的導體,在 ![]() 時刻可能有
時刻可能有 ![]() 個電子發生碰撞,碰撞『平均時距』的『系綜平均』是
個電子發生碰撞,碰撞『平均時距』的『系綜平均』是
![]()
。比之於《【Sonic π】電路學之補充《一》》一文中之電子的『時間平均值』,果然這兩者相等。事實上一般物理系統要是處於統計力學所說的『平衡狀態』,這兩種『平均值』都會是『相等』的。當真是『考典範以歷史』與『察大眾於一時』都能得到相同結論的嗎??
─── 摘自《【Sonic π】電路學之補充《二》》



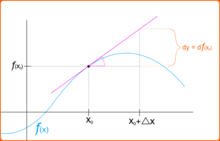
 在點
在點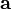 處
處 下降最快。
下降最快。
 為一個夠小數值時成立,那麼
為一個夠小數值時成立,那麼 。
。 的局部極小值的初始估計
的局部極小值的初始估計 出發,並考慮如下序列
出發,並考慮如下序列  使得
使得 。
。
 收斂到期望的極值。注意每次疊代步長
收斂到期望的極值。注意每次疊代步長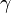 可以改變。
可以改變。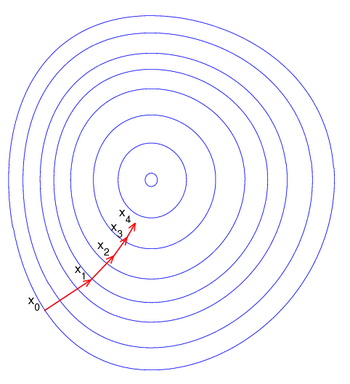
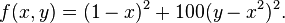
 處,數值為
處,數值為 。但是此函數具有狹窄彎曲的山谷,最小值
。但是此函數具有狹窄彎曲的山谷,最小值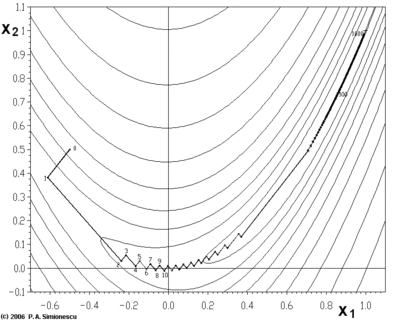
 ,則
,則![\varphi\left(\mathbf{q}\right)-\varphi\left(\mathbf{p}\right) = \int_{\gamma[\mathbf{p},\,\mathbf{q}]} \nabla\varphi(\mathbf{r})\cdot d\mathbf{r}.](https://upload.wikimedia.org/math/c/a/8/ca8b2c89c9693e534bf73ab7c65d411f.png)
 維空間中的曲線。
維空間中的曲線。 是
是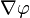 就是
就是
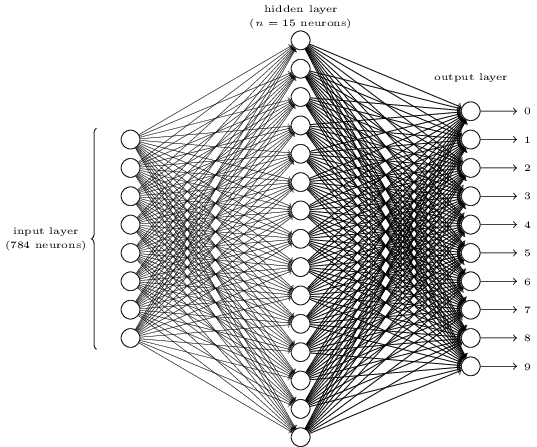


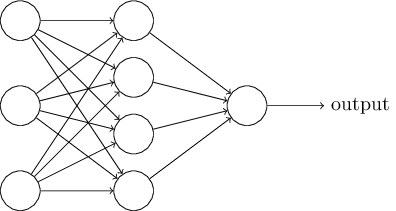
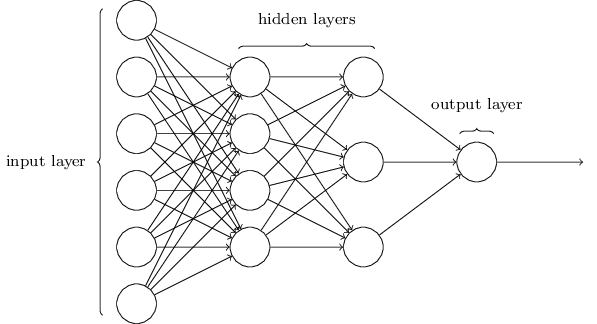

![Rendered by QuickLaTeX.com python3 Python 3.2.3 (default, Mar 1 2013, 11:53:50) [GCC 4.6.3] on linux2 Type "help", "copyright", "credits" or "license" for more information. # 定義站站間『連接』事實 >>> from pyDatalog import pyDatalog >>> pyDatalog.create_terms('連接, 鄰近, 能達, 所有路徑') >>> +連接('台北車站', '中山') >>> +連接('台北車站', '善導寺') >>> +連接('台北車站', '西門') >>> +連接('台北車站', '台大醫院') >>> +連接('西門', '龍山寺') >>> +連接('西門', '小南門') >>> +連接('西門', '北門') >>> +連接('中山', '北門') >>> +連接('中山', '雙連') >>> +連接('中山', '松江南京') >>> +連接('中正紀念堂', '小南門') >>> +連接('中正紀念堂', '台大醫院') >>> +連接('中正紀念堂', '東門') >>> +連接('中正紀念堂', '古亭') >>> +連接('東門', '古亭') >>> +連接('東門', '忠孝新生') >>> +連接('東門', '大安森林公園') >>> +連接('善導寺', '忠孝新生') >>> +連接('松江南京', '忠孝新生') >>> +連接('忠孝復興', '忠孝新生') >>> +連接('松江南京', '行天宮') >>> +連接('松江南京', '南京復興') >>> +連接('中山國中', '南京復興') >>> +連接('台北小巨蛋', '南京復興') >>> +連接('忠孝復興', '南京復興') >>> +連接('忠孝復興', '忠孝敦化') >>> +連接('忠孝復興', '大安') >>> +連接('大安森林公園', '大安') >>> +連接('科技大樓', '大安') >>> +連接('信義安和', '大安') >>> +連接('信義安和', '世貿台北101') >>> </pre> 此處『連接』次序是『隨興』輸入的,一因『網路圖』沒有個經典次序,次因『事實』『陳述』不會因次序而改變,再 因『程序』上『pyDatalog』對此『事實』『次序』也並不要求。由於『連接』之次序有『起止』方向性,上面的陳述並不能代表那個『捷運網』,這可以 從下面程式片段得知。【<span style="color: #808080;">※ 在 pyDatalog 中,沒有變元的『查詢』 ask or query ,以輸出『set([()]) 』表示一個存在的事實,以輸出『None』表達所查詢的不是個事實。</span>】 <pre class="lang:sh decode:true"># 單向性 >>> pyDatalog.ask("連接('信義安和', '世貿台北101')") == set([()]) True >>> pyDatalog.ask("連接('世貿台北101', '信義安和')") == set([()]) False >>> pyDatalog.ask("連接('世貿台北101', '信義安和')") == None True >>> </pre> 所以我們必須給定『連接( □, ○)』是具有『雙向性』的,也就是 <span style="color: #ff9900;">連接<span class="crayon-sy">(</span><span class="crayon-i">X</span>站名<span class="crayon-sy">,</span><span class="crayon-i">Y</span>站名<span class="crayon-sy">)</span><span class="crayon-o"><=</span>連接<span class="crayon-sy">(</span><span class="crayon-i">Y</span>站名<span class="crayon-sy">,</span><span class="crayon-i">X</span>站名<span class="crayon-sy">)</span></span> ,這樣的『規則』 Rule 。由於 pyDatalog 的『語詞』 Term 使用前都必須『宣告』,而且『變元』必須『大寫開頭』,因此我們得用 <span style="color: #ff9900;">pyDatalog.create_terms('X站名, Y站名, Z站名, P路徑甲, P路徑乙')</span> 這樣的『陳述句』 Statement。【<span style="color: #808080;">※ 中文沒有大小寫,也許全部被當成了小寫,所以變元不得不以英文大寫起頭。</span>】 ─── 摘自《<a href="http://www.freesandal.org/?p=37256">勇闖新世界︰ 《 pyDatalog 》 導引《七》</a>》 <span style="color: #666699;">假使細思](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-f6d2dbbf270540e1b076e54dab9f778c_l3.png) z_j = \sum_i w_{ji} \cdot x_i + b_j$ 表達式,或許自可發現『 S 神經元』網絡計算與『矩陣』數學密切關聯︰
z_j = \sum_i w_{ji} \cdot x_i + b_j$ 表達式,或許自可發現『 S 神經元』網絡計算與『矩陣』數學密切關聯︰



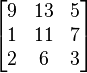

 with multiplication as composition is
with multiplication as composition is