每日彙整: 2017-08-08

樹莓派、樹莓派之學習、樹莓派之教育

GoPiGo 小汽車︰格點圖像算術《投影幾何》【四‧平面國】《壬》

《Cut The Knot》網站上有一篇文章介紹了『交比』︰

Cross-Ratio

The cross-ratio is a surprising and a fundamental concept that plays a key role in projective geometry. In the spirit of duality, cross-ratio is defined for two sets of objects: 4 collinear points and 4 concurrent lines.

The cross-ratio (ABCD) of four collinear points A, B, C, D is defined as the “double ratio”:

(1)

(ABCD) = CA/CB : DA/DB,

where all the segments are thought to be signed. The cross-ratio obviously does not depend on the selected direction of the line ABCD, but does depend on the relative position of the points and the order in which they are listed.

The cross-ratio (abcd) of four (coplanar and) concurrent lines is defined as another double ratio, now of sines:

(abcd) = sin(cMa)/sin(cMb) : sin(dMa)/sin(dMb),

where angles are also considered signed (in a natural way.) If points A, B, C, D are chosen on four lines a, b, c, d concurrent at M, then we often write (abcd) = M(ABCD). The fact that the four points (lines) are grouped into two pairs of points (lines) is reflected in another popular notation: (AB; CD) and (ab; cd).

The relationship between the two definitions is established by the following

Lemma

Let A, B, C, D be the points of intersection of 4 concurrent lines a, b, c, d by another straight line. Then (ABCD) = (abcd).

Remark

When the lines a, b, c, d are defined by the points, as above, it is often convenient to write (abcd) = M(ABCD).

Proof of Lemma

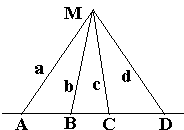
Consider 4 triangles CMA, CMB, DMA, and DMB and represent their areas in two different ways:

  Area(CMA): h·CA/2 = MC·MA·sin(CMA)/2
  Area(CMB): h·CB/2 = MC·MB·sin(CMB)/2
  Area(DMA): h·DA/2 = MD·MA·sin(DMA)/2
  Area(DMB): h·DB/2 = MD·MB·sin(DMB)/2,

where h is the length of the common altitude of the four triangles from vertex M. The required identity now follows immediately.

The lemma helps explain the significance of the cross-ratio in projective geometry.

Theorem 1

The cross-ratio of collinear points does not change under central (and, trivially, parallel) projections.

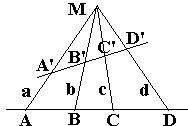
Indeed, from Lemma, (ABCD) = (abcd) = (A’B’C’D’).

It’s worth noting that central projection does not, in general, preserve either the distance or the ratio of two distances.

A permutation of the points may or may not change the cross-ratio. If any two pairs of points are swaped simultaneously, the cross-ratio does not change, e.g., (ABCD) = (BADC) = (DCBA). Wherever it changes, there are only five possible values. If (ABCD) = m, the possible values are 1-m, 1/m, (m-1)/m, 1/(1-m), m/(m-1).

If (ABCD) = 1, then either A = B or C = D. A more important case is where (ABCD) = -1. If (ABCD) = -1 then the points C and D are called harmonic conjugates of each other with respect to the pair A and B. A and B are then also harmonic conjugates with respect to C and D. Each of the pairs is said to divide the other’s segment harmonically. There exists a straight edge only construction of harmonic conjugates. The four lines through an arbitrary point M and four conjugate points are called a harmonic bundle.

One of the four points may lie at infinity. On such occasions, it is useful to consider the limit when a finite point moves to infinity along the common line of the four. The limit is quite simple. For example, if D = , then (ABC) = CA/CB.

The theorem has been established by Pappus in the seventh book of his Mathematical Collections. It was further developed by Desargues starting with 1639 [Wells, p. 41].

 

或許可當作探索『幾何意義』的起點。首先為什麼『交比』又稱為『雙比』 double ratio 呢？因為 (ABCD) \equiv (A, B ; C, D) =_{df} \frac{CA}{CB} : \frac{DA}{DB} 是『比之比』。這建議了『比』之『定義』可由三『共線點』(A, B; C) = \frac{CA}{CB} 給出，因此『交比』 (A, B; C, D) 就是 \frac{(A, B ; C)}{(A, B ; D)} 的了。

那麼這個『比』 (A, B ; C) 有什麼『幾何意義』嗎？事實上它可以用來『確定』直線 \overline {AB} 上任意點 C 的『位置』。甚至賦予『座標數值』 ── AC 、BC 同向取正，反向取負 ── 。如果與『共點』 M 線結合起來︰

 

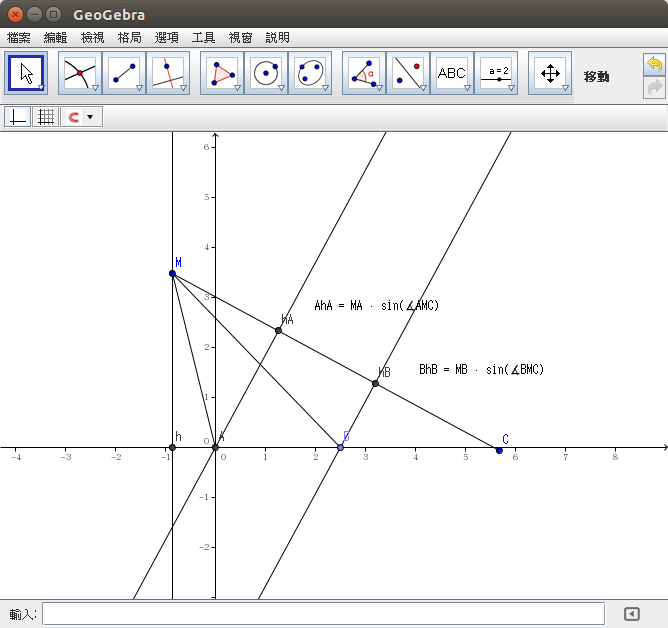
可得『邊』、『角』對應關係︰

\triangle MAC 之面積 I = \frac{1}{2} CA \cdot Mh = \frac{1}{2} MA \cdot \sin(\angle AMC) \cdot MC 。

\triangle MBC 之面積 II = \frac{1}{2} CB \cdot Mh = \frac{1}{2} MB \cdot \sin(\angle BMC) \cdot MC 。

\frac{I}{II} = \frac{CA}{CB} = \frac{MA}{MB} \cdot \frac{\sin(\angle AMC) }{\sin(\angle BMC)} 。

故知對固定之『共點』 M 與『定點』 A, B 而言，『邊角比』

\frac{CA}{CB} : \frac{\sin(\angle AMC) }{\sin(\angle BMC)} = \frac{MA}{MB} 和 C 點的『位置無關』也。

此乃『交比不變性』之基礎吧！

也許該想想它與

正弦定理

正弦定理是三角學中的一個定理。它指出：對於任意  \triangle ABC，  a、  b、  c分別為  \angle A、  \angle B、  \angle C的對邊，  R為  \triangle ABC的外接圓半徑，則有

  {\displaystyle {\frac {a}{\sin \angle A}}={\frac {b}{\sin \angle B}}={\frac {c}{\sin \angle C}}=2R}

 

有無邏輯淵源哩？

如果已知『共點投影』之『交比不變』，是否能夠證明『投影調和共軛』條件乎？！

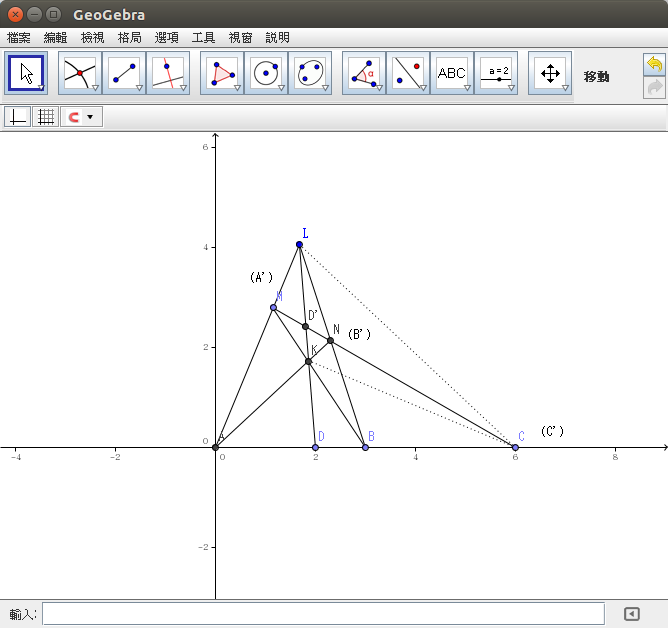
Projective harmonic conjugate

In projective geometry, the harmonic conjugate point of an ordered triple of points on the real projective line is defined by the following construction:

Given three collinear points A, B, C, let L be a point not lying on their join and let any line through C meet LA, LB at M, N respectively. If AN and BM meet at K, and LK meets AB at D, then D is called the harmonic conjugate of C with respect to A, B.[1]

The point D does not depend on what point L is taken initially, nor upon what line through C is used to find M and N. This fact follows from Desargues theorem; it can also be defined in terms of the cross-ratio as (A, B; C, D) = −1.

 

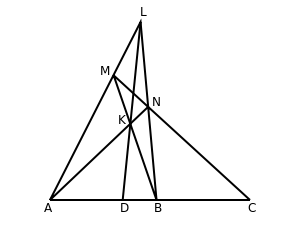
D is the harmonic conjugate of C w.r.t. A and B.
A, D, B, C form a harmonic range.
KLMN is a complete quadrangle generating it.

 

※ 注 L, K 都是『交比』共點◎