每日彙整: 2017-08-03

樹莓派、樹莓派之學習、樹莓派之教育

GoPiGo 小汽車︰格點圖像算術《投影幾何》【四‧平面國】《戊》

□︰人工智慧之見，是善？是惡？

○︰非善非惡，器用無記。神、魔之為定數也。人之所作或然矣。恐乎近魔？

□︰不能神耶！

○︰非不能也，不為也。

○︰神者，坤之祀，法地禮天而已。苟不愛其土，果能為哉？

 

物理天地原有，本之以為發明，豈非自然乎？如是奈何心中不安！『物用』、『用物』之術常生分殊耶！？

正所以假

《時間序列︰阿涅西的女巫》

文本再次重申

‧ 如何深入了解一個重要的定律︰

大數定律

在數學與統計學中，大數定律又稱大數法則、大數律，是描述相當多次數重複實驗的結果的定律。根據這個定律知道，樣本數量越多 ，則其平均就越趨近期望值。

大數定律很重要，因為它「保證」了一些隨機事件的均值的長期穩定性。人們發現，在重複試驗中，隨著試驗次數的增加，事件發生的頻率趨於一個穩定值；人們同時也發現，在對物理量的測量實踐中，測定值的算術平均也具有穩定性。比如，我們向上拋一枚硬幣 ，硬幣落下後哪一面朝上本來是偶然的，但當我們上拋硬幣的次數足夠多後，達到上萬次甚至幾十萬幾百萬次以後，我們就會發現，硬幣每一面向上的次數約占總次數的二分之一。偶然之中包含著必然。

切比雪夫定理的一個特殊情況、辛欽定理和伯努利大數定律都概括了這一現象，都稱為大數定律。

表現形式

大數定律主要有兩種表現形式：弱大數定律和強大數定律。定律的兩種形式都肯定無疑地表明，樣本均值

{\overline {X}}_{n}={\frac {1}{n}}(X_{1}+\cdots +X_{n})

收斂於真值

{\overline {X}}_{n}\,\to \,\mu \qquad {\textrm {for}}\qquad n\to \infty ,

其中 X1, X2, … 是獨立同分布的，期望值 E(X1) = E(X2) = …= µ 的，勒貝格可積的隨機變量構成的無窮序列。Xj 的勒貝格可積性意味著期望值 E(Xj) 存在且有限。

方差 Var(X1) = Var(X2) = … = σ2 < ∞ 有限的假設是非必要的。很大或者無窮大的方差會使其收斂得緩慢一些，但大數定律仍然成立。通常採用這個假設來使證明更加簡潔。

強和弱之間的差別在所斷言的收斂的方式。對於這些方式的解釋，參見隨機變量的收斂。

‧ 有時候不只要知道它的推導過程︰…

‧ 還要能知道有沒有反例︰…

‧ 清楚明白違背的理由︰…

‧ 且試著追溯它的歷史︰

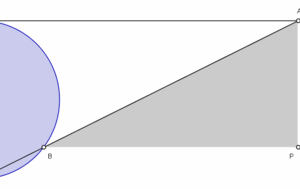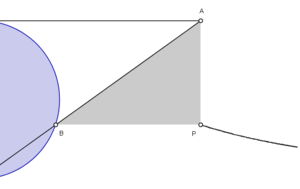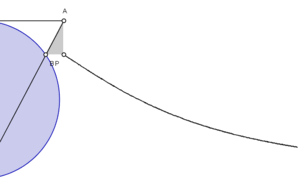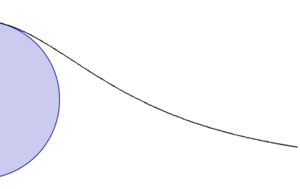
箕舌線

箕舌線是平面曲線的一種，也被稱為阿涅西的女巫（英語：The Witch of Agnesi）[1][2][3]。

給定一個圓和圓上的一點O。對於圓上的任何其它點A，作割線OA。設M是O的對稱點。OA與M的切線相交於N。過N且與OM平行的直線，與過A且與OM垂直的直線相交於P。則P的軌跡就是箕舌線。

箕舌線有一條漸近線，它是上述給定圓過O點的切線。

方程

設O是原點，M在正的y軸上。假設圓的半徑是a。

則曲線的方程為  {\displaystyle y={\frac {8a^{3}}{x^{2}+4a^{2}}}}。

注意如果a=1/2，則曲線化為最簡單的形式： {\displaystyle y={\frac {1}{x^{2}+1}}.}

如果  \theta \,是OM與OA的夾角，則曲線的參數方程為：

{\displaystyle x=2a\tan \theta ,\ y=2a\cos ^{2}\theta .\,}

如果  \theta \,是OA與x軸的夾角，則曲線的參數方程為：

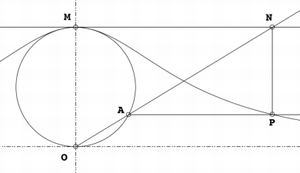
{\displaystyle x=2a\cot \theta ,\ y=2a\sin ^{2}\theta .\,}

箕舌線

歷史

皮埃爾·德·費馬曾在1630年研究這條曲線。1703年時格蘭迪提出了建構這條曲線的方法。1718年時格蘭迪建議將這條曲線命名為versoria，意思是張帆的繩子，並將這條曲線的義大利文名稱命名為versiera[4]

1748年時瑪利亞·阿涅西出版了著名的著作《Instituzioni analitiche ad uso della gioventù italiana》，其中箕舌線仍沿用格蘭迪取的名稱versiera[4]，一恰好當時的義大利文Aversiera/Versiera是衍生自拉丁文的Adversarius，是魔鬼的一個稱呼「與神為敵的」，和女巫是同義詞[5]。也許因為這個原因，劍橋教授 約翰·科爾森就誤譯了這條曲線。許多近代有關阿涅西及此曲線的著作對於誤譯的原因有些不同的猜測[6][7][8]斯特洛伊克認為：

versiera這個字是衍生自拉丁文的vertere，但後者也是義大利文avversiera（女魔鬼）的縮寫。英格蘭有些聰敏者將之翻譯成女巫（英語：witch），而這好笑的雙關語仍存於多數的英文教材裡。在費馬的著作（Oeuvres, I, 279-280; III, 233-234）就已經出現這條曲線，其名稱versiera是格蘭迪取的，在牛頓的曲線分類中，它是第63類……第一個使用女巫來描述這條曲線的可能是威廉森在1875年的《Integral calculus》中首次使用[9]

另一方面，史蒂芬·史蒂格勒認為是格蘭迪自已在玩文字遊戲[10]。

應用

箕舌線除了其理論的性質外．也常出現在現實生活中．不過這次應用是在20世紀末期及21世紀才有足夠的了解。在為一些物體現象建立數學模型時，會出現箕舌線[11]。 此方程式近似光線及X光的譜線分布，也是共振電路中的能量耗散量。

箕舌線和柯西分布的機率密度函數有相同的形式。

光滑小山嶽的截面也類似箕舌線。在數學建模中已用箕舌線作為一種流場的障礙物[12][13]。

‧ 確定論理之條件︰…

 

談談『平面國』耳熟能詳之『統通哲學』︰

能統此，故通彼。

的『觀點』。

其幸存之《平面國數典》的『聯星‧平行』詞條記載曰︰

物遠則迷離，眼見不分明，度量有取捨，因此『聯星』擬『平行』義也。

設若 \overline{EF} 為直徑，繞圓心 D 逆旋，因著點 F 遙遠之故﹐位於 A 處的理想觀察者之度量將為 (\frac{r \cdot \cos(\theta)}{d + r \cdot \sin(\theta)}, 1) 。當此遙遠 d >> r 之際， \frac{1}{d + r \cdot \sin(\theta)} \approx \frac{1}{d} ，故而宛如 (r \cdot \cos(\theta), d) 於 D, y = d 處之平行投影 。實與聯星近處之觀察者所見數據有差異也。

 

※ 註

雙星 (天文)

雙星是觀測天文學的名詞，當兩顆恆星由地球上觀察時，在視線的方向上非常接近，以致以肉眼看起來像是只有一顆恆星，但使用望遠鏡時就能分辨出來是一對的恆星。這種情形可以發生在一對聯星，也就是有著互動的軌道，並且被彼此的重力束縛在一起；也可以是光學雙星，這是兩顆有這不同的距離，但恰巧在天空中相同的方向上被對準在一起[1][2]。聯星對恆星天文學家是很重要的，當知道它們的運動，就可以直接計算它們的質量和其它地恆星參數。 從1780年代開始，研究雙星的專業和業餘天文學家就透過望遠鏡的觀測量雙星之間的距離和角度，以量度每一對雙星之間的相對運動[3]。如果測量出的相對運動是一段軌道弧線，或者相對運動相較於這兩顆恆星本身的一般自行是很小的值，就可以得到這兩顆恆星沒有相互的軌道運動。換言之，這一對就只是光學雙星[2]。雖然多顆的恆星系統的運動比聯星更為複雜，但對聚星的研究也是用這種方法。

成對的恆星有下列三種：

  • 光學雙星：是無關聯的恆星 － 只是從地球看過去他們恰好對齊在一起；
  • 目視聯星 － 被重力束縛在一起，使用光學望遠鏡就可以分辨的恆星；
  • 非目視聯星 － 要使用更專業的工具，像是掩星（食雙星）、光譜（光譜聯星）、或異常的自行（天測聯星）才能分辨的聯星。

就觀念而言，後面這兩種之間其實沒有差別。望遠鏡的改進可以將非目視聯星重分類至目視聯星中，像北極星在2006年就發生這種情形。因此，第三種只是我們在觀測方法上的不同造成的區別。