藉著引進『單位尺』   度量平面，

然後思考什麼『變』了，什麼『不變』的呢？

pi@raspberrypi:~  \left( \begin{array}{cc} A & 0 \\ C & D \end{array} \right) l \to l^{'}\left( \begin{array}{cc} \frac{b}{a} & 0 \\ \frac{1- \frac{1}{k}}{a} & \frac{1}{k}  \end{array} \right)\overline{AB}\ddaggera=1, \ \left( \begin{array}{cc} \frac{b}{a} & 0 \\ \frac{1- \frac{1}{k}}{a} & \frac{1}{k}  \end{array} \right) \Rightarrow \ \left( \begin{array}{cc} b & 0 \\ 1- \frac{1}{k} & \frac{1}{k}  \end{array} \right) = \left( \begin{array}{cc} b & 0 \\ 0 & 1 \end{array} \right)   \  \left( \begin{array}{cc} 1 & 0 \\ 1- \frac{1}{k} & \frac{1}{k}  \end{array} \right) l=1BAsll^{'}A^{'}sa,b(x_{\Box}, t_{\Box})(x_{\bigcirc}, t_{\bigcirc})v\begin{bmatrix} x_{\bigcirc} \\ t_{\bigcirc} \end{bmatrix} = G_v \begin{bmatrix} x_{\Box} \\ t_{\Box} \end{bmatrix} = \begin{pmatrix} 1 & -v \\0 & 1 \end{pmatrix} \begin{bmatrix} x_{\Box} \\ t_{\Box} \end{bmatrix}(0, t_{\Box})x_{\bigcirc} = - v \cdot t_{\Box}t_{\bigcirc} = t_{\Box}v(x_{\Box}^1, t_{\Box})(x_{\Box}^2, t_{\Box})(x_{\Box}^1 - v \cdot t_{\Box}, t_{\Box})(x_{\Box}^2 - v \cdot t_{\Box}, t_{\Box})\begin{bmatrix} x_{\Box} \\ t_{\Box} \end{bmatrix} = G_{-v} \begin{bmatrix} x_{\bigcirc} \\ t_{\bigcirc} \end{bmatrix} G_{-v} = {G_v}^{-1} = \begin{pmatrix} 1 & v \\0 & 1 \end{pmatrix}\begin{pmatrix} 1 & v \\0 & 1 \end{pmatrix} \times \begin{pmatrix} 1 & - v \\0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & - v \\0 & 1 \end{pmatrix} \times \begin{pmatrix} 1 & v \\0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\0 & 1 \end{pmatrix}(x_{\star}, t_{\star})w\begin{bmatrix} x_{\bigcirc} \\ t_{\bigcirc} \end{bmatrix} = G_v \begin{bmatrix} x_{\Box} \\ t_{\Box} \end{bmatrix} = \begin{pmatrix} 1 & -v \\0 & 1 \end{pmatrix} \begin{bmatrix} x_{\Box} \\ t_{\Box} \end{bmatrix}\begin{bmatrix} x_{\star} \\ t_{\star} \end{bmatrix} = G_w \begin{bmatrix} x_{\bigcirc} \\ t_{\bigcirc} \end{bmatrix} = \begin{pmatrix} 1 & -w \\0 & 1 \end{pmatrix} \begin{bmatrix} x_{\bigcirc} \\ t_{\bigcirc} \end{bmatrix}=  \begin{pmatrix} 1 & -w \\0 & 1 \end{pmatrix} \times \begin{pmatrix} 1 & -v \\0 & 1 \end{pmatrix} \begin{bmatrix} x_{\Box} \\ t_{\Box} \end{bmatrix}=  \begin{pmatrix} 1 & -(w+v) \\0 & 1 \end{pmatrix} \begin{bmatrix} x_{\Box} \\ t_{\Box} \end{bmatrix}=  G_{(w+v)} \begin{bmatrix} x_{\Box} \\ t_{\Box} \end{bmatrix}\begin{bmatrix} x_{\bigcirc} \\ t_{\bigcirc} \end{bmatrix} =  L_v \begin{bmatrix} x \\ t \end{bmatrix} = \frac{1}{\sqrt{1 - {(\frac{v}{c})}^2}}  \begin{pmatrix} 1 & -v \\ -\frac{v}{c^2} & 1 \end{pmatrix} \begin{bmatrix} x_{\Box} \\ t_{\Box} \end{bmatrix}-\frac{v}{c^2} L_{- v} = L_{v}^{-1}L_w \cdot L_v = L_{w \bigoplus v} = \frac{1}{\sqrt{1 - {[\frac{(w+v)/c}{1+(wv/c^2)}]}^2}}  \begin{pmatrix} 1 & -[\frac{(w+v)}{1+(wv/c^2)}] \\ -\frac{1}{c^2} {[\frac{(w+v)}{1+(wv/c^2)}]}^2 & 1 \end{pmatrix} \begin{bmatrix} x_{\Box} \\ t_{\Box} \end{bmatrix}\neq L_{(w + v)} \begin{bmatrix} x_{\Box} \\ t_{\Box} \end{bmatrix}w \bigoplus v = \frac{w + v}{1 + (w v / c^2)}L_{w \bigoplus v}  = \frac{1}{\sqrt{1 - {(\frac{(w \bigoplus v)}{c})}^2}}  \begin{pmatrix} 1 & -(w \bigoplus v) \\ -\frac{(w \bigoplus v)}{c^2} & 1 \end{pmatrix} $ 這又能有什麼『不對』的嗎？因是之故，『狹義相對論』所帶來的『困惑』遠勝於『運動之不可能性』，反倒以為『運動』果真能是這種『現象』的嘛！！



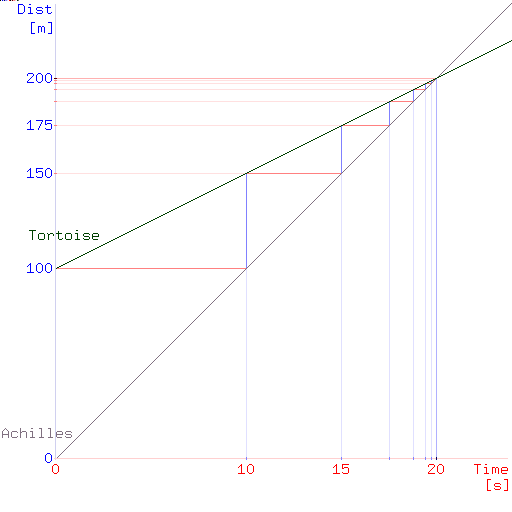
果真『阿基里斯』 Achilles 追得上『烏龜』，然而這件事又怎麽『可能』用著『數理邏輯』來『證明』的呢？假使說『大自然』果是『如是』，我們卻『不要』『如是』的『相信』，那麼我們『該用』什麼『道理』來『論辯』的呢？？偉大的科學家『愛因斯坦』說︰我會為親愛的上帝感到遺憾。不管怎樣理論都還是正確的。



誰趕的上芝諾的烏龜呢？


─── 摘自《【Sonic π】電聲學之電路學《四》之《 !!!! 》下》