天下皆知美之為美，斯惡已；皆知善之為善，斯不善已。故有無相生，難易相成，長短相形，高下相傾，音聲相和，前後相隨。

是以聖人處無為之事，行不言之教。萬物作焉而不辭，生而不有，為而不恃，功成而弗居。夫唯弗居，是以不去。

何謂『矛盾』的呢？『此』且『非此』，『彼』又『非彼』一類的『概念』。若問『善』與『惡』是『矛盾』的嗎？假使人世間有『不善不惡』之事或『既善且惡』之行，當然『善‧ 惡』就不可說是邏輯的『矛盾』。即使沒有『又善又惡』的事件，那『善‧惡』的概念是否就可窮盡一切現象哩！要是存在『無記』之『非善非惡』的作為，那『善‧惡』依然不可說是邏輯的『矛盾』！！

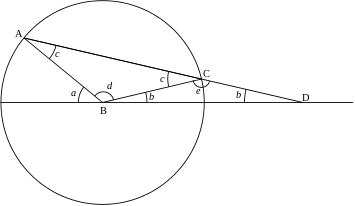
讀者莫要以為『透視』在『二維』平面上的表達就一定比『三維』空間裡容易？如果說 $\overline{z_1 z_2}$ 是一條『投影線』︰

代數上講可用 $(1 - \lambda) z_1 + \lambda z_2, \ \lambda \in Real$ 表示也。此時平面上之『任一點』 $z$ 與這條『投影線』可有多種關係︰

‧I︰ $z = z_1$ 或 $z = z_2$ 。

‧II︰ $z$ 不在『投影線』上，但在 $\overline{Pz_1}$ 或 $\overline{Pz_2}$ 『視線』上。

‧III︰非 I 且 II ， $z$ 在『投影線』上。

‧IV:︰非 I、II、III 之『投影線』外一點。

此所以前一篇寫來總覺拗口為難矣︰

【相依三點】 $z_1 = x_1 + y_1 \cdot i , \ z_2 = x_2 + y_2 \cdot i, \ z_3 = x_3 + y_3 \cdot i , \ det_{12}, det_{13}, det_{23} \neq 0$ 。

如果 $a \cdot z_1 + b \cdot z_2 = - c \cdot z_3$ ，當下

$\right) \left( \begin{array}{cc} a \\ b \end{array} \right) = - c {\left( \begin{array}{cc} x_1 & x_2 \\ y_1 & y_2 \end{array} \right)}^{-1} \left( \begin{array}{cc} x_3 \\ y_3 \end{array} \right)$ 。

豈能『不相依』耶！◎

假設 $c = -1$ ，上式不過是說平面裡『任一點』 $z$ ，都可以用『任選兩個』 $z_1, z_2$ 『線性獨立』向量所構成 $z = \alpha \cdot z_1 + \beta \cdot z_2$ 。若講這 $(\alpha, \beta)$ 一般也稱作『廣義座標』︰

Generalized coordinates

In analytical mechanics, specifically the study of the rigid body dynamics of multibody systems, the term generalized coordinates refers to the parameters that describe the configuration of the system relative to some reference configuration. These parameters must uniquely define the configuration of the system relative to the reference configuration.^[1] This is done assuming that this can be done with a single chart. The generalized velocities are the time derivatives of the generalized coordinates of the system.

An example of a generalized coordinate is the angle that locates a point moving on a circle. The adjective “generalized” distinguishes these parameters from the traditional use of the term coordinate to refer to Cartesian coordinates: for example, describing the location of the point on the circle using x and y coordinates.

Although there may be many choices for generalized coordinates for a physical system, parameters which are convenient are usually selected for the specification of the configuration of the system and which make the solution of its equations of motion easier. If these parameters are independent of one another, the number of independent generalized coordinates is defined by the number of degrees of freedom of the system.^[2]^[3]

首要『二維』『自由度』不變也。

此時如果

$\alpha + \beta \neq 1$ ，

$z$ 怎麼可能在 $\overline{z_1 z_2}$ 線上耶？？

然而 $\overline{Pz}$ 『視線』 $\lambda \cdot z = \lambda \cdot \alpha \cdot z_1 + \lambda \cdot \beta \cdot z_2$ 終有

$\lambda \cdot \alpha + \lambda \cdot \beta = 1$ 時乎！！

解析者務請小心也★☆

俗話說︰不以規矩，不足以成方圓。在西方文明史中，這個僅使用『直尺』與『圓規』來『作圖』的傳統實在是淵源流長的，據聞它是來自於古希臘的『數學課題』，而且只准用『圓規』和『直尺』，並且祇能在『有限次』的『操作』裡，去解決各種不同的平面幾何『作圖題』。還有人講，它還有『抽象』的『限制條件』︰

一、直尺沒有刻度，但可以是『無限長』，而且只能夠使用直尺之固定的一側。它的『作用』可以將『已有』的『兩個點』連接在一起，成為一條『線』。

二、圓規所畫的圓能夠達半徑長『無限寬』，但是上面也不可以刻有『角度』。它的主要製圖『作用』是『複製』已有的『長度』或是產生與其它之『線』或者『圓』彼此之間的『交點』。

這引發了『古希臘三大難題』
一、【化圓為方】
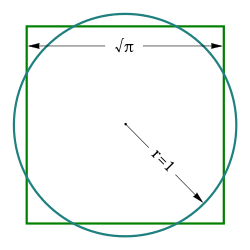
求一個正方形的邊長，使它的面積與一個已知的圓相等。
二、【三等分角】
求一角，使它的角度是一個已知角度的三分之一。
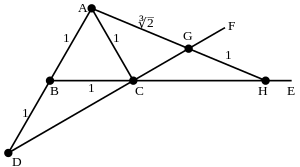
三、【倍立方】
求一立方體的邊長，使它的體積是一個已知立方體的二倍。

經過了上千年的努力，人們開始思考這些『問題』的『可行性』之『條件』，假使我們按造它規定所說的『條件』，這些都是『不可能』被『作出來』的了。這又是為什麼的呢？因為假使只使用『線』與『圓』，如果從『解析幾何』的觀點來看，『尺規作圖』 Compass-and-straightedge construction 最多也只能夠是多個『二次方程式』之『疊套』 $a_1 + b_1 \sqrt{a_2 + b_2 \sqrt{a_3 + b_3 \sqrt{\dots}}}$ 的罷了！若是有『不滿足』這個『條件』的『構圖』，難到它是有『可能』的『作出圖』的嗎？？

比方說『化圓為方』的方程式像是 $x^2 = \pi r^2$ ，不要說 $\sqrt{\pi}$ 畫不畫的出來，那個 $\pi$ 難道就畫的出來的嗎？如果思考一個『單位圓』 ── 直徑等於一，圓周長等於 $\pi$ ── 的『內接』以及『外切』的正四邊形、八邊形、十六邊形等等『倍邊數』逼近的『正多邊形』，這個圓的『周長』 $\pi$ 總是介於這些內外的『正多邊形』之『周長』之間，就算那些內外切『正多邊形』都可以借助於『半角公式』 $\sin\frac{\theta}{2}=\pm\sqrt\frac{1-\cos\theta}{2}$ 表達成『二次方程式』的『疊套』形式，恐怕也得要『無限』之『尺規步驟』才能得出這個 $\pi$ 的吧！

雖然我們已經談過了『三次方程式』的求解以及一般方程式『二次方根』解的個數是『偶數』的，如果我們直接計算 $\sqrt[3]{r} = a + b \sqrt{Q}, \ Q \geq 0$ 會得到什麼的呢？
$r = {(a + b \sqrt{Q})}^3$
$= a^3 + 3 a^2 b \sqrt{Q} + 3 a b^2 Q + b^3 Q \sqrt{Q}$
$= (a^3 + 3 a b^2 Q) + (3 a^2 b + b^3 Q) \sqrt{Q}$
$\therefore 3 a^2 b + b^3 Q = 0$
，所以 $3 a^2 + b^2 Q = 0$ ，因為 $a^2, b^2 > 0$ ，所以 $Q < 0$ ，這就產生了假設『矛盾』的了，因此『立方根』終究是無法表達成『二次方根』的吧！！

假使我們從『三角函數』的『三倍角公式』來看
$\cos \theta = 4 \cos^3 {\frac{\theta}{3}} -3 \cos {\frac{\theta}{3}}$
，這又是一個『三次方程式』的啊！無怪乎，它也是『幾何作圖』之『不可能』的吧！！