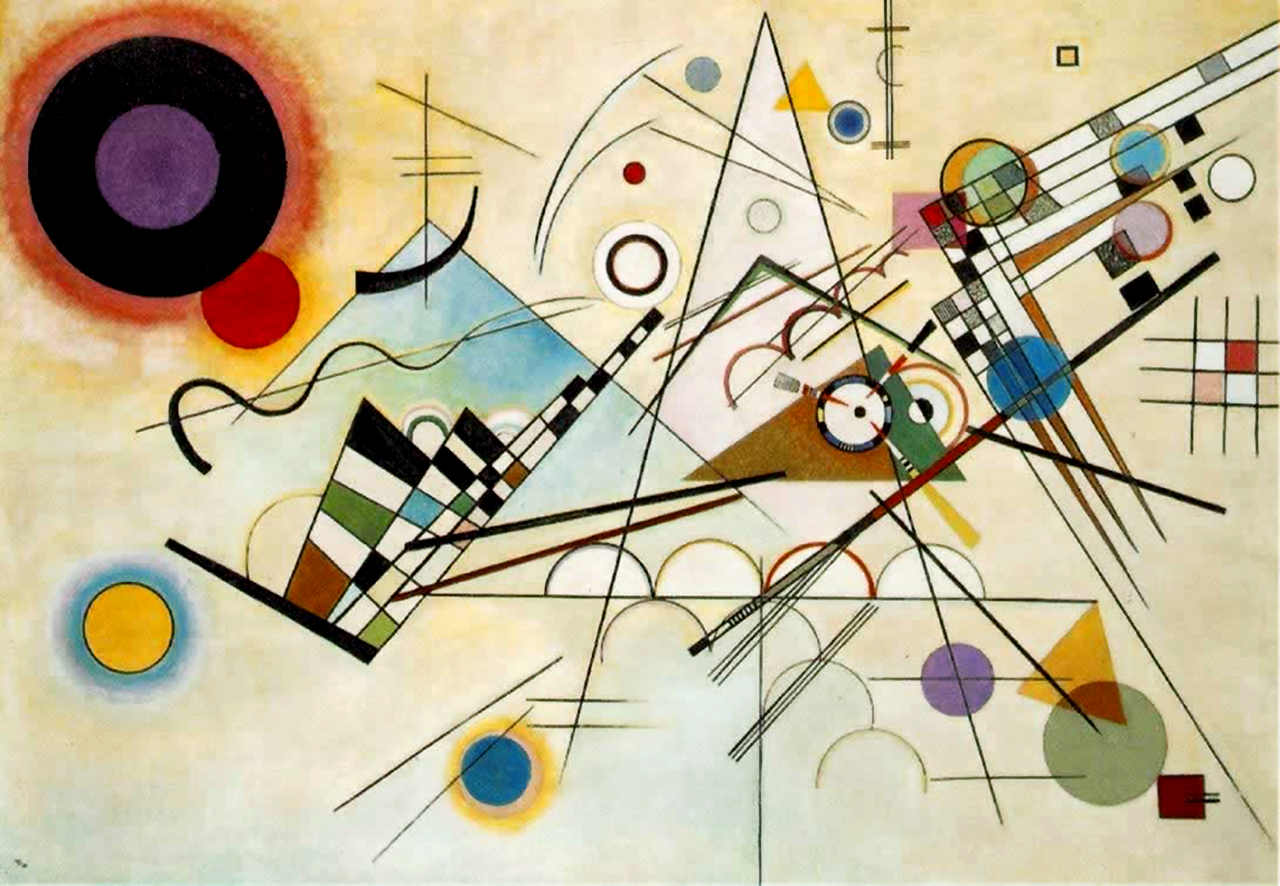
當我們不明白書籍『文字所指』之時,容易『望文生義』。
【孫子歌】
三人同行七十稀,
五樹梅花廿一枝,
七子團圓正半月,
除百零五便得知。
其實是說『餘數定理』的例子 ,不過彷彿『雞同鴨講』罷了︰
《孫子算經‧序》孫子曰:
夫算者,天地之經緯,群生之元首;五常之本末,陰陽之父母;星辰之建號,三光之表裹;五行之準平,四時之終始;萬物之祖宗,六藝之綱紀。 稽群倫之聚散,考二氣之降升;推寒暑之迭運,步遠近之殊同;觀天道精微之兆基,察地理從橫之長短;采神祇之所在,極成敗之符驗;窮道德之 理,究性命之情。立規矩,準方圓,謹法度,約尺丈,立權衡,平重輕,剖毫釐,析黍絫;歷億載而不朽,施八極而無疆。散之不可勝究,斂之不盈掌握。嚮之者富 有餘,背之者貧且窶;心開者幼沖而即悟,意閉者皓首而難精。夫欲學之者必務量能揆己,志在所專。如是則焉有不成者哉。
南宋時的數學家秦九韶著作《數書九章》內有『大衍求一術』,正好用來『解詩』,『七十』除三餘一,卻為『五、七』整除;『二十一』除五餘一,卻為『三、七』整除;『十五』除七餘一,卻為『三、五』整除;三數的最小公倍數『三乘五乘七』是為『百零五』,所以答案是 ![]() 。『科技』與『人文』難道一定是『南轅北轍』不能『對話共歌』的嗎??
。『科技』與『人文』難道一定是『南轅北轍』不能『對話共歌』的嗎??
就像皮亞諾之『後繼數』概念,似乎太過『抽象』而不自然一般︰
義大利的數學家朱塞佩‧皮亞諾 Giuseppe Peano 提出『自然數』之五條公設的系統。用著『未定義』的『基元』數『零 ![]() 』,以及『後繼數』successor 的概念,打造了一階算術系統,現今稱之為『皮亞諾算術系統』︰
』,以及『後繼數』successor 的概念,打造了一階算術系統,現今稱之為『皮亞諾算術系統』︰
一、 ![]() 是自然數。
是自然數。
二、 如果 ![]() 是自然數,則
是自然數,則 ![]() 的後繼數也是自然數。
的後繼數也是自然數。
三、 ![]() 不是任何自然數的後繼數。
不是任何自然數的後繼數。
四、 如果兩個自然數的後繼數相等,則這兩個自然數相等。
五、 任何關於自然數的命題,假使證明了這個命題對於自然數 ![]() 是真的,如果它對自然數
是真的,如果它對自然數 ![]() 為真時,又可以證明它對
為真時,又可以證明它對 ![]() 後繼數也真,那麼這個命題對所有的自然數都是真的── 數學歸納法 ──。
後繼數也真,那麼這個命題對所有的自然數都是真的── 數學歸納法 ──。
於是可以將皮亞諾算術表達成︰此處 ![]() 代表某數之後繼數
代表某數之後繼數
![]()
![]()
![]() ,就是數學歸納法
,就是數學歸納法
![]()
![]()
![]()
![]()
─── 摘自《λ 運算︰計物數《上》》
也許那個『寫實』之『投影』,才會如此難以掌握哩。
【越調】天淨沙‧秋思
元 馬致遠
枯籐老樹昏鴉,
小橋流水人家,
古道西風瘦馬。
夕陽西下,
斷腸人在天涯。
繪畫、照片與書法是哪種比較『寫實』?哪個又較為『抽象』?《秋思》中用具象《『藤』、『樹』、『鴉』》,來虛寫『時光變化』之《『枯』、『老』、『昏』》;以實景《『橋』、『水』、『家』》,將串成『應歸之所』的《『小』、『流』、『人』》;終至於『道』得『古』、『風』是『西』、『馬』又怎能不『廋』?此刻也許只該是『夕陽西下』??否則哪歸結的出『胡不歸去』之『斷腸人在天涯』!!
或許『失重』的『實物』漂浮於天之涯海之角,反而更顯得『虛幻』的了!!而『抽象』的『圖形』一旦擬似具體構物,或會因『沈重』終將失去『空靈』的嗎??
─── 摘自《λ 運算︰計物數《中》》
若知維基百科這段『射影』 Projection (mathematics) 文字
In mathematics, a projection is a mapping of a set (or other mathematical structure) into a subset (or sub-structure), which is equal to its square for mapping composition (or, in other words, which is idempotent). The restriction to a subspace of a projection is also called a projection, even if the idempotence property is lost.
實寫『投影』之『同名異物』
‧ 平面 → 投影線
‧ 投影線 → 投影線
或可解惑乎?★
所謂【平面 → 投影線】
此講
投影
在線性代數和泛函分析中,投影是從向量空間映射到自身的一種線性變換,是日常生活中「平行投影」概念的形式化和一般化。同現實中陽光將事物投影到地面上一樣,投影變換將整個向量空間映射到它的其中一個子空間,並且在這個子空間中是恆等變換[1]。
定義
投影的嚴格定義是:一個從向量空間 V 射到它自身的線性變換 P 是投影,若且唯若 。另外一個定義則較為直觀:P 是投影,若且唯若存在 V 的一個子空間 W ,使得 P 將所有V中的元素都映射到 W 中,而且 P 在 W 上是恆等變換。用數學的語言描述,就是:
-
,使得
,並且
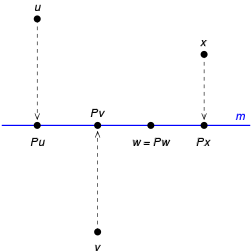
變換 P 是在線 m 上的正交投影。
簡單例子
在現實生活中,陽光在地面上留下各種影子。這就是投影變換最直白的例子。可以理想化地假設陽光都是沿著同一個方向(比如說垂直於地面的角度)照射而來,大地是嚴格的平面,那麼,對於任意一個物體(比如說一隻正在飛行的鳥),它的位置可以用向量 (x, y, z) 來表示,而這隻鳥在陽光下對應著一個影子,也就是 (x, y, 0)。這樣的一個變換就是一個投影變換。它將三維空間中的向量 (x, y, z) 到映射到向量 (x, y, 0) 。這是在 x–y 平面上的投影。這個變換可以用矩陣表示為
因為對任意一個向量 (x, y, z) ,這個矩陣的作用是:
注意到如果一個向量原來就是表示地面上的一點的話(也就是說它的z分量等於0),那麼經過變換 P 後不會有改變。也就是說這個變換在子空間 x–y 平面上是恆等變換,這證明了 P 的確是一個投影。
另外,
所以 P = P2,這也證明 P 的確是投影。
『直觀義』也。固然 ![]() 的『空間維度』大於等於
的『空間維度』大於等於 ![]() ,通常之義
,通常之義 ![]() ,一般故是『多對一』之『映射』 Map (mathematics) 耶!所以沒有『反函數』乎?
,一般故是『多對一』之『映射』 Map (mathematics) 耶!所以沒有『反函數』乎?
因此『以義求義』,『中心投射』 central projection 『定義』是將任意一條通過『觀察者』之『原點』的整條『射線』 ray ![]() 上的『所有點』
上的『所有點』 ![]() 『映射』到『投影線』之『某一點』
『映射』到『投影線』之『某一點』 ![]() 當然無法反演矣!
當然無法反演矣!
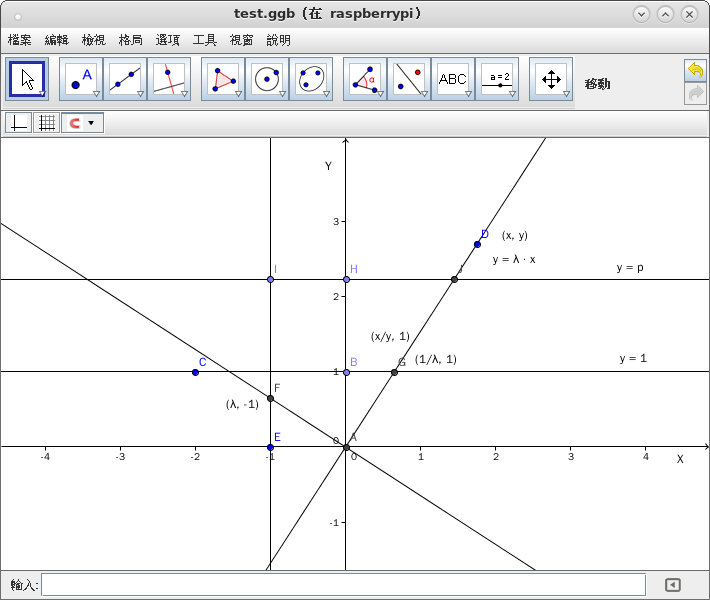
此義傳言《平面國數典》之斷簡殘篇記載為『相對』於『觀察者』之『數』。
且借該國言傳道
【投影線 → 投影線】
吧!
眾『物』處世界中,非人之所為,故以之為『客觀』也。『觀者』亦眾,各有『度量數據』,皆是自然之『相對』觀點。況『物』有『動靜』 , 察有『座標』。祇是『幾何』旨在『不變性』,正所以『投影』研究『數據』間的『恆常關係』矣。
見圖類推自識自知焉◎
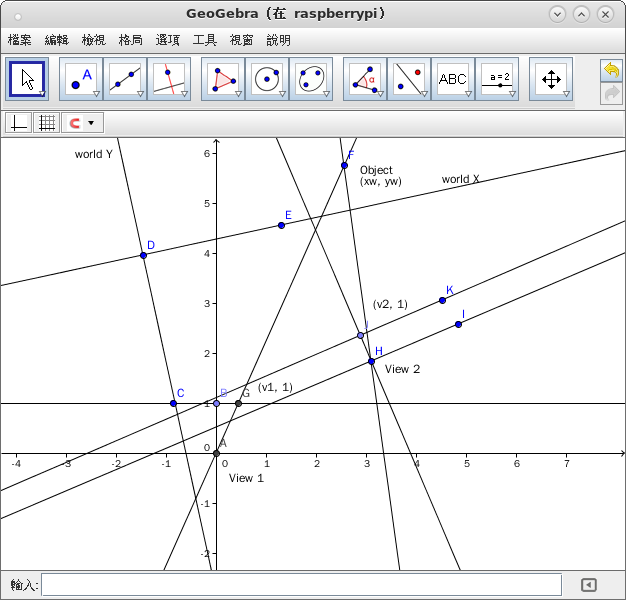
誠可務本立基呦☆
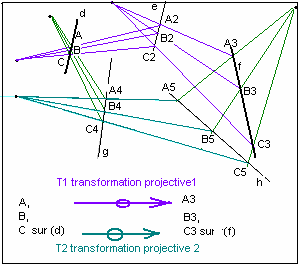
The Fundamental Theory of Projective Geometry