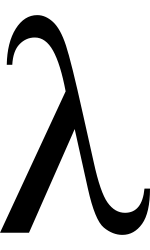λ 表達式的『核心』理念是︰將『函數』應用於其『引數』;藉『抽象』形成『函數』。用著『簡潔』的『語法』,專注於『表徵』函數;視『函數』為計算的『規則』,深得『計算』之『內蘊』。其『語詞』表達『疏落』大方,概念『表現力』與『柔軔性』十足。故為『邏輯』、『數學』和『程式』理念之『聚寶盆』!!
辨明『異同』與分解『差別』是學習的功夫︰
真積力,久則入。
讓我們再次『觀止』λ 表達式的『定義』︰
變元集合 ![]()
抽象符號 『 λ 』與『 . 』,符號本身不是λ 表達項
結構括號 『 ( 』與『 ) 』,括號本身不是λ 表達項
λ 表達式的論域集合 ![]() ,由下面三條語法歸納定義︰
,由下面三條語法歸納定義︰
一、如果 ![]() ,那麼
,那麼 ![]()
二、如果 ![]() 而且
而且 ![]() ,那麼
,那麼 ![]()
三、如果 ![]() ,那麼
,那麼 ![]()
假 使觀察一個合乎語法的 λ 表達式 ![]() ,然後問著『
,然後問著『 ![]() 』變元是指『什麼』?這個表達式最內層的
』變元是指『什麼』?這個表達式最內層的 ![]() 是函式的應用,明寫
是函式的應用,明寫 ![]() 是某個函式,然而如何計算卻隻字未提。如此看來,所謂的『變元』也可以是『函式』。那要怎麼『詮釋』那個『 λ表達式』呢?由於我們不知道
是某個函式,然而如何計算卻隻字未提。如此看來,所謂的『變元』也可以是『函式』。那要怎麼『詮釋』那個『 λ表達式』呢?由於我們不知道 ![]() 指的是什麼?也可以說它們『未被定義』,假使『給與定義』,我們或許可以講『在這個解釋下』,該個『 λ表達式』的『語意』是『□□□』。比方談著『用量角器量角度』一事,假使︰
指的是什麼?也可以說它們『未被定義』,假使『給與定義』,我們或許可以講『在這個解釋下』,該個『 λ表達式』的『語意』是『□□□』。比方談著『用量角器量角度』一事,假使︰
![]() 用量角器量角度
用量角器量角度
![]() 東西的角度
東西的角度
,那麼 ![]() 是說︰拿某種『待指定』的量角器來量『尚未說』之物的角度。
是說︰拿某種『待指定』的量角器來量『尚未說』之物的角度。
要是講到『計算某種三角函數的數值』時,設想︰
![]() 某種三角函數的計算
某種三角函數的計算
![]() 角度
角度
,那麼 ![]() 是說︰用某個『待指定』的三角函數來計算『未輸入』的角度。
是說︰用某個『待指定』的三角函數來計算『未輸入』的角度。
……
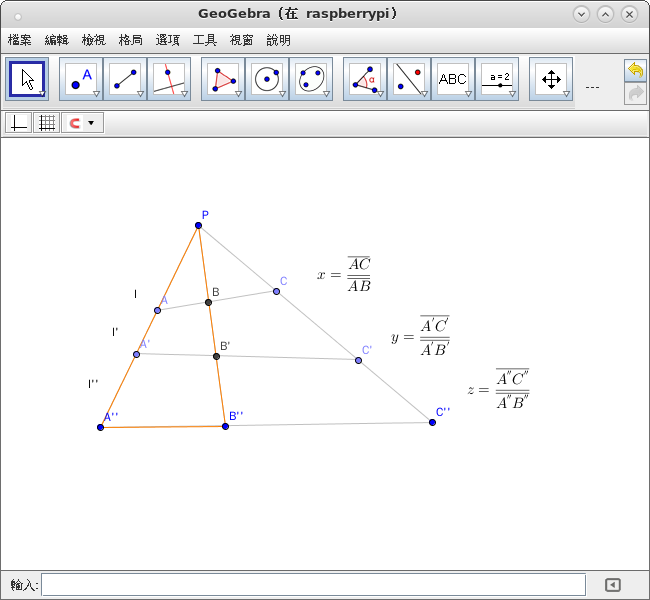
面對『抽象』表達式,若是缺少直覺之『詮釋』導引,還真不曉得該看什麼、做什麼呢?舉例而言︰
設有 ![]() 兩線,而且
兩線,而且 ![]() 與
與 ![]() 是那兩線上共線和對應之三點。已知
是那兩線上共線和對應之三點。已知 ![]() ,那麼這兩線之間形成透視關係,同時滿足『分式線性變換』形式。
,那麼這兩線之間形成透視關係,同時滿足『分式線性變換』形式。

可得
![]()
![]() 也。
也。
這個 ![]() ,簡單計算可知
,簡單計算可知
![]() 。
。
然而所謂的『透視』,意義不止如此,將要如何『觀』耶?假設 ![]() 線上有一『代表點』
線上有一『代表點』 ![]() ,那麼
,那麼
![]()
![]()
![]()
![]() 式除了可用來確定
式除了可用來確定
![]() 外,重要的是
外,重要的是
![]() 之意義。
之意義。
要是想求 ![]() 線上的『無窮遠點』
線上的『無窮遠點』 ![]() 之『對應點』,
之『對應點』, ![]() 式比較好使吧!此時
式比較好使吧!此時
![]() 。
。
那它有什麼『奧秘』嗎??首先 ![]() 這向量與
這向量與 ![]() 『平行』,既在
『平行』,既在 ![]() 線上,一般不在
線上,一般不在 ![]() 線上!此也可由『套套邏輯』
線上!此也可由『套套邏輯』
![]()
![]() 確證也!!
確證也!!
那點難到不是『平行』於 ![]() 之『視線』和
之『視線』和 ![]() 線之『交會點』乎?? !!如果
線之『交會點』乎?? !!如果
![]() ,
,
想必讀者可以推知其意義吧!!??
既然已將『對射』性質賦予『透視』,![]() 投影點
投影點 ![]() 間之對應關係可用
間之對應關係可用
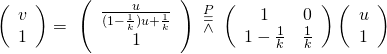 或
或
![]()
『齊次座標』表達也。
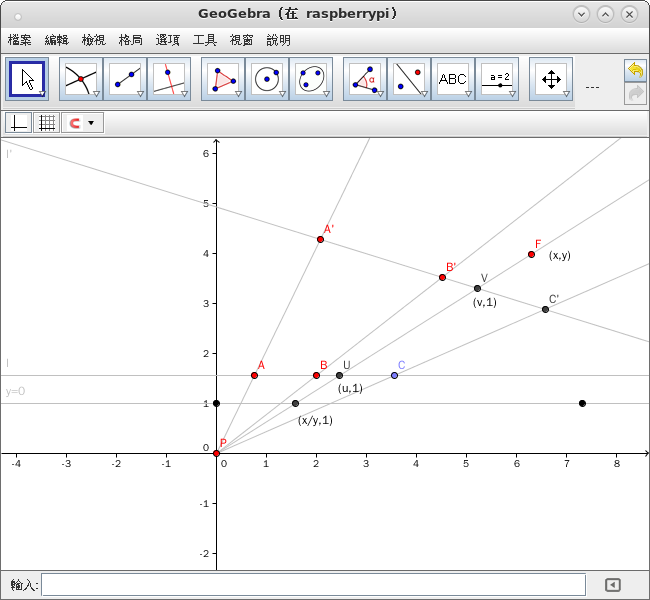
從表達式可知我們仍舊取 ![]() 為『定點』︰
為『定點』︰
![]() ,
,![]() 。
。
簡單計算可得︰
![]() ,
,![]() 。
。
而且還是用『本地座標系』︰
![]() 是線
是線 ![]() 上的『單位長度』,
上的『單位長度』, ![]() 。對應之
。對應之
![]() 是線
是線 ![]() 上的『單位長度』,
上的『單位長度』,![]() 。
。
![]() 為此一『透視』下之『常數』︰
為此一『透視』下之『常數』︰
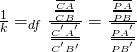 。
。
且先看看這個『矩陣形制』滿足『透視』之『對合』嗎?假設線 ![]() 趨近於
趨近於 ![]() 將『重合』,那麼那個『矩陣形制』會是
將『重合』,那麼那個『矩陣形制』會是 ![]() 『單位矩陣』乎??
『單位矩陣』乎??
當此時刻 ![]() 必然趨近於
必然趨近於 ![]() 哩!焉能不是
哩!焉能不是 ![]() 耶!!
耶!!
但思 ![]() 之條件不必是『重合』矣,難到不能是『平行』
之條件不必是『重合』矣,難到不能是『平行』 ![]() 嘛?!
嘛?!
古來『平行』費疑猜!?實因『眼見為憑』有此『遠近之事』吧★
…
過 ![]() 點平行
點平行 ![]() 之線,將交
之線,將交 ![]() 於無窮遠
於無窮遠 ![]() 處,但交
處,但交 ![]() 於
於
![]() ,反之依然
,反之依然
過 ![]() 點平行
點平行 ![]() 之線,將交
之線,將交 ![]() 於無窮遠
於無窮遠 ![]() 處,但交
處,但交 ![]() 於
於
![]() 。
。
招手『無限』 ![]() 說何事?『平行』本性自帶來!
說何事?『平行』本性自帶來!
![]() ;
;
![]() 。
。
終究根源自家栽
![]() ◎
◎
─── 摘自《GoPiGo 小汽車︰格點圖像算術《投影幾何》【五‧線性代數】《導引六‧中》》