17 | 9 月 | 2017 | FreeSandal

屠龍刀

論語‧《陽貨》

子之武城，聞弦歌之聲。夫子莞爾而笑，曰：「割雞焉用牛刀？」子游對曰：「昔者偃也聞諸夫子曰：『君子學道則愛人，小人學道則易使也。』」子曰：「二三子！偃之言是也。前言戲之耳。」

所謂『相由心生』是說精神外顯的『形貌』從『用心方向』而來，這個『習焉不察』之內在『心相』，常可以用來分辨『行業』。一行有一行的規矩，百業有百業的訣竅，入了行，從了業，自然帶有某種『氣息』的吧！如何才能夠不著『相』？若可『無所住』而生其『心』，那麼既無『我心』何來『我相』的呢！！

那麼這個《子之武城》一事，是否有個『前言』對上『後語』，可分出『對錯好壞』的呢？也許有個『禮樂』之『理』和『禮樂』之『用』的差別，想那『子游』為武城宰，採用『禮樂』教化之道，孔夫子卻『莞爾』笑，豈有不『以子之言，擊子之語』的哩！然而夫子所謂『戲之』果真是說『割雞焉用牛刀？』是錯了嗎？恐是不樂見『禮樂』被當作了『名器』的吧！就像到了宋代的『存天理，去人欲』，導致『死生事小，失節事大』，終演成『禮教殺人』之憾事！！於是

祇『能』這樣『用』，不『會』那樣『使』，終究難了『用大』之道 ── 無用而不通達 ── ，如如不動，應事而動，因事制宜。

正說著『以正治國』和『以奇用兵』，『為學之法』與『用學之法』的不同，也須避免那『紙上談兵』之過。此事《孫子兵法》

地形‧第十

孫子曰：地形有通者、有掛者、有支者、有隘者、有險者、有遠者。我可以往，彼可以來，曰通。通形者，先居高陽，利糧道，以戰則利。可以往，難以返，曰掛。掛形者，敵無備，出而勝之，敵若有備，出而不勝，難以返，不利。我出而不利，彼出而不利，曰支。支形者，敵雖利我，我無出也，引而去之，令敵半出而擊之，利。隘形者，我先居之，必盈之以待敵。若敵先居之，盈而勿從，不盈而從之。險形者，我先居之，必居高陽以待敵；若敵先居之，引而去之，勿從也。遠形者，勢均，難以挑戰，戰而不利。凡此六者，地之道也，將之至任，不可不察也。

故兵有走者、有弛者、有陷者、有崩者、有亂者、有北者。凡此六者，非天之災，將之過也。夫勢均，以一擊十，曰走；卒強吏弱，曰馳；吏強卒弱，曰陷；大吏怒而不服，遇敵懟而自戰，將不知其能，曰崩；將弱不嚴，教道不明，吏卒無常，陳兵縱橫，曰亂；將不能料敵，以少合衆，以弱擊強，兵無選鋒，曰北。凡此六者，敗之道也，將之至任，不可不察也。

夫地形者，兵之助也。料敵制勝，計險厄遠近，上將之道也。知此而用戰者必勝，不知此而用戰者必敗。故戰道必勝，主曰無戰，必戰可也；戰道不勝，主曰必戰，無戰可也。故進不求名，退不避罪，唯民是保，而利合於主，國之寶也。

視卒如嬰兒，故可以與之赴深溪；視卒如愛子，故可與之俱死。厚而不能使，愛而不能令，亂而不能治，譬若驕子，不可用也。

知吾卒之可以擊，而不知敵之不可擊，勝之半也；知敵之可擊，而不知吾卒之不可以擊，勝之半也；知敵之可擊，知吾卒之可以擊，而不知地形之不可以戰，勝之半也。故知兵者，動而不迷，舉而不窮。故曰：知彼知己，勝乃不殆；知天知地，勝乃可全。

講的好。

─── 《字詞網絡︰ WordNet 《六》相 □ 而用 ○ ！！》

假使說『形勢』比人強！那麼『形式』無所言耶？

就算『滿天變數』！！只要『彼此相關』？？並非『無所拘束』乎！！？？

Specifying a transformation by three points

Given a set of three distinct points z₁, z₂, z₃ on the Riemann sphere and a second set of distinct points w₁, w₂, w₃, there exists precisely one Möbius transformation f(z) with f(z_i) = w_i for i = 1,2,3. (In other words: the action of the Möbius group on the Riemann sphere is sharply 3-transitive.) There are several ways to determine f(z) from the given sets of points.

Mapping first to 0, 1, ∞

It is easy to check that the Möbius transformation

f_{1}(z)={\frac {(z-z_{1})(z_{2}-z_{3})}{(z-z_{3})(z_{2}-z_{1})}}

with matrix

{\mathfrak {H}}_{1}={\begin{pmatrix}z_{2}-z_{3}&-z_{1}(z_{2}-z_{3})\\z_{2}-z_{1}&-z_{3}(z_{2}-z_{1})\end{pmatrix}}

maps z₁, z₂, z₃ to 0, 1, ∞, respectively. If one of the z_i is ∞, then the proper formula for ${\mathfrak {H}}_{1}$ is obtained from the above one by first dividing all entries by z_i and then taking the limit z_i → ∞.

If ${\mathfrak {H}}_{2}$ is similarly defined to map w₁, w₂, w₃ to 0, 1, ∞, then the matrix ${\mathfrak {H}}$ which maps z_1,2,3 to w_1,2,3 becomes

{\mathfrak {H}}={\mathfrak {H}}_{2}^{{-1}}{\mathfrak {H}}_{1}.

The stabilizer of {0, 1, ∞} (as an unordered set) is a subgroup known as the anharmonic group.

縱使只一『式』 $\frac{(z - z_1)(z_2 - z_3)}{(z - z_3)(z_2 - z_1)}$ ，亦『勢』必將有所決矣︰

由於實難知能否破『迷惘』？？！！

故而明指『任意』『三相異點』 $z_1,z_2,z_3$ 之 $0,1,\infty$ 的『投射』

${\mathfrak {H}}_{1} = \left( \begin{array}{cc} z_2 - z_3 & - z_1(z_2-z_3) \\ z_2 - z_1 & -z_3(z_2-z_1) \end{array} \right)$

真地存在呦☆

應該怎麼講

$\left( \begin{array}{cc} \frac{z_2 - z_3}{z_2-z_1} & - \frac{z_1(z_2-z_3)}{z_2-z_1} \\ 1 & -z_3 \end{array} \right)$

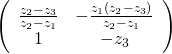
之所指哩★

如是再借

${\mathfrak {H}}_{2} = \left( \begin{array}{cc} w_2 - w_3 & - w_1(w_2-w_3) \\ w_2 - w_1 & -w_3(w_2-w_1) \end{array} \right)$

，求得 ${{\mathfrak {H}}_{2}}^{-1} \cdot {\mathfrak {H}}_{1}$ ，

豈非『任意』三點『投射』到『任意』三點呀◎

pi@raspberrypi:~ $ ipython3
Python 3.4.2 (default, Oct 19 2014, 13:31:11) 
Type "copyright", "credits" or "license" for more information.

IPython 2.3.0 -- An enhanced Interactive Python.
?         -> Introduction and overview of IPython's features.
%quickref -> Quick reference.
help      -> Python's own help system.
object?   -> Details about 'object', use 'object??' for extra details.

In [1]: from sympy import *

In [2]: init_printing()

In [3]: z1,z2,z3,w1,w2,w3 = symbols('z1,z2,z3,w1,w2,w3')

In [4]: H1 = Matrix([[z2-z3,-z1*(z2-z3)],[z2-z1,-z3*(z2-z1)]])

In [5]: H1
Out[5]: 
⎡z₂ - z₃   -z₁⋅(z₂ - z₃) ⎤
⎢                        ⎥
⎣-z₁ + z₂  -z₃⋅(-z₁ + z₂)⎦

In [6]: H2 = Matrix([[w2-w3,-w1*(w2-w3)],[w2-w1,-w3*(w2-w1)]])

In [7]: H2
Out[7]: 
⎡w₂ - w₃   -w₁⋅(w₂ - w₃) ⎤
⎢                        ⎥
⎣-w₁ + w₂  -w₃⋅(-w₁ + w₂)⎦

In [8]: H2反矩陣 = H2.inv()

In [9]: H2反矩陣 = Matrix([[H2反矩陣[0,0].simplify(), H2反矩陣[0,1].simplify()],[H2反矩陣[1,0].simplify(), H2反矩陣[1,1].simplify()]])

In [10]: H2反矩陣
Out[10]: 
⎡        -w₃                  -w₁        ⎤
⎢───────────────────  ───────────────────⎥
⎢(w₁ - w₃)⋅(w₂ - w₃)  (w₁ - w₂)⋅(w₁ - w₃)⎥
⎢                                        ⎥
⎢        -1                   -1         ⎥
⎢───────────────────  ───────────────────⎥
⎣(w₁ - w₃)⋅(w₂ - w₃)  (w₁ - w₂)⋅(w₁ - w₃)⎦

In [11]: H = H2反矩陣 * H1

In [12]: H[0,0].simplify()
Out[12]: 
w₁⋅(w₂ - w₃)⋅(z₁ - z₂) - w₃⋅(w₁ - w₂)⋅(z₂ - z₃)
───────────────────────────────────────────────
         (w₁ - w₂)⋅(w₁ - w₃)⋅(w₂ - w₃)         

In [13]: H[0,1].simplify()
Out[13]: 
-w₁⋅z₃⋅(w₂ - w₃)⋅(z₁ - z₂) + w₃⋅z₁⋅(w₁ - w₂)⋅(z₂ - z₃)
──────────────────────────────────────────────────────
            (w₁ - w₂)⋅(w₁ - w₃)⋅(w₂ - w₃)             

In [14]: H[1,0].simplify()
Out[14]: 
(w₁ - w₂)⋅(-z₂ + z₃) + (w₂ - w₃)⋅(z₁ - z₂)
──────────────────────────────────────────
      (w₁ - w₂)⋅(w₁ - w₃)⋅(w₂ - w₃)       

In [15]: H[1,1].simplify()
Out[15]: 
z₁⋅(w₁ - w₂)⋅(z₂ - z₃) - z₃⋅(w₂ - w₃)⋅(z₁ - z₂)
───────────────────────────────────────────────
         (w₁ - w₂)⋅(w₁ - w₃)⋅(w₂ - w₃)         

In [16]: H[1,1].simplify() / H[1,0].simplify()
Out[16]: 
z₁⋅(w₁ - w₂)⋅(z₂ - z₃) - z₃⋅(w₂ - w₃)⋅(z₁ - z₂)
───────────────────────────────────────────────
   (w₁ - w₂)⋅(-z₂ + z₃) + (w₂ - w₃)⋅(z₁ - z₂)  

In [17]:

日	一	二	三	四	五	六
« 8 月				10 月 »
					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30

FreeSandal

每日彙整: 2017-09-17

GoPiGo 小汽車︰格點圖像算術《投影幾何》【五‧線性代數】《導引七‧變換組合 VIII‧⚄ 》

Specifying a transformation by three points

Mapping first to 0, 1, ∞

輕。鬆。學。部落客