每日彙整: 2017-09-28

樹莓派、樹莓派之學習、樹莓派之教育

GoPiGo 小汽車︰格點圖像算術《投影幾何》【五‧線性代數】《導引八》觀察者《變換‧C 》

由於現今尚未有『未來』之『名目』，即使 W!o+ 願說想說，怕也是『說不得』的吧！！

220px-Reading_VOG_hor
Horizontal eye movement in reading. Left-to-right movement may be seen as “upstairs”, and right-to-left saccades 【掃視】are clear.

EyeFixationsReading
A diagram demonstrating the acuity 【清晰度】of foveal vision in reading

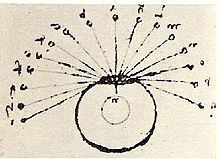
220px-Eye_Line_of_sight
Leonardo da Vinci: The eye has a central line 【中間線】and everything that reaches the eye through this central line can be seen distinctly.

東西方人看待『事物』的『視線』 line-of-sight 常取不同的『方向』，如今『中文橫寫』已經成為主流，但是我們並不知道『去經存緯』的改變，是否會產生什麼樣的『讀‧解』變化？畢竟『閱讀中的眼睛』 Eye movement in reading 之『運動』，可是與『認知』活動息息相關的ㄚ！

要是【明月當空】 W!o 是指那千古一遇之『曌』── 一代女皇武則天獨創之字 ──，意味著『日月明空曌』，那麼

【朋比翼鳥】是『鵬』；

【社神廢祀】為『坤】；

這可是『鯤鵬巨變』的呀！一旦發生就『回不去』了！！難怪得斷之以

【有始無終】。

那其它的『辭意』呢？或『有意』，或『無意』，或『自生其意』的耶？？

『會‧通』的講︰ W!o 說︰效法

《莊子‧逍遙游》

北冥有魚，其名為鯤。鯤之大，不知其幾千里也。化而為鳥，其名為鵬。鵬之背，不知其幾千里也；怒而飛，其翼若垂天之雲。是鳥也，海運則將徙於南冥。南冥者，天池也。

齊諧者，志怪者也。諧之言曰：「鵬之徙於南冥也，水擊三千里，摶扶搖而上者九萬里，去以六月息者也。」野馬也，塵埃也，生物之以息相吹也。天之蒼蒼，其正色邪？其遠而無所至極邪？其視下也，亦若是則已矣。

且夫水之積也不厚，則其負大舟也無力。覆杯水於坳堂之上，則芥為之舟；置杯焉則膠，水淺而舟大也。風之積也不厚，則其負大翼也無力。故九萬里，則風斯在下矣，而後乃今培風，背負青天而莫之夭閼者，而後乃今將圖南。

蜩與學鳩笑之曰：「我決起而飛，搶榆枋，時則不至而控於地而已矣，奚以之九萬里而南為？」適莽蒼者，三飡而反，腹猶果然；適百里者，宿舂糧；適千里者，三月聚糧。之二蟲又何知？

小知不及大知，小年不及大年。奚以知其然也？朝菌不知晦朔，蟪蛄不知春秋，此小年也。楚之南有冥靈者，以五百歲為春，五百歲為秋；上古有大椿者，以八千歲為春，八千歲為秋。此大年也。而彭祖乃今以久特聞，眾人匹之，不亦悲乎！

……

，愛上『派生』 Python ，自然創生『 M♪o 踢呦ㄊㄜˋ』！！！

─── 《怎樣詮釋 W!o+ 之信息？？下》

 

視線在其方向上無遠弗屆，故難論距離矣。若以共點言，可否保角耶？

共形映射

數學上，共形變換（英語：Conformal map）或稱保角變換，來自於流體力學和幾何學的概念，是一個保持角度不變的映射。

更正式的說，一個映射

  w=f(z)\,

稱為在  z_{0}\, 共形(或者保角)，如果它保持穿過  z_{0}\, 的曲線間的定向角度，以及它們的取向也就是說方向。共形變換保持了角度以及無窮小物體的形狀，但是不一定保持它們的尺寸。

共形的性質可以用坐標變換的導數矩陣雅可比矩陣的術語來表述。如果變換的雅可比矩陣處處都是一個純量乘以一個旋轉矩陣，則變換是共形的。

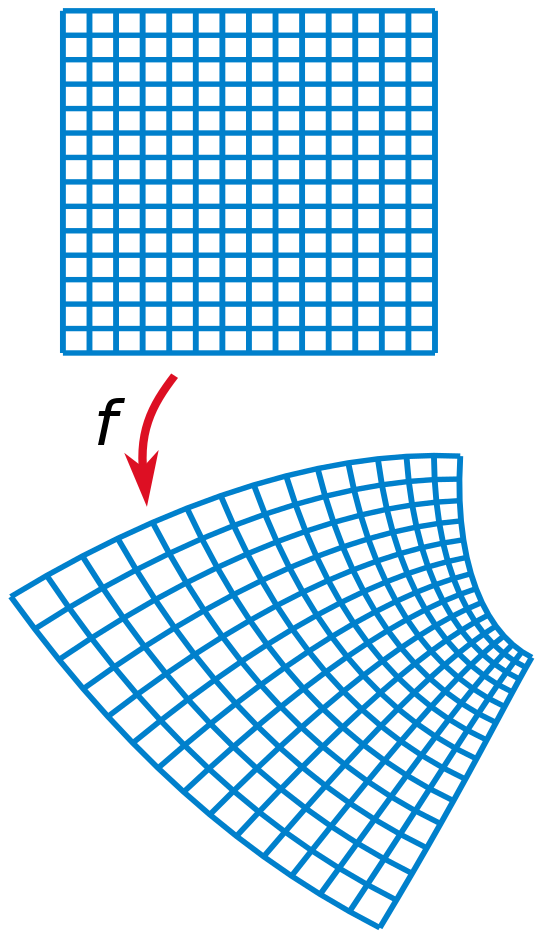
直角網格(頂部)和它在共形映射 f 下的像(底部)。可看出 f 把以 90°相交的成對的線映射成仍以 90°相交的成對曲線。

 

設使角都不可保，那麼怎有透視，交比可論乎？？此誠複變分析中之美妙也！

Complex analysis

“Complex analytic” redirects here. For the class of functions often called “complex analytic”, see Holomorphic function.

Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including algebraic geometry, number theory, analytic combinatorics, applied mathematics; as well as in physics, including the branches of hydrodynamics, thermodynamics, and particularly quantum mechanics. By extension, use of complex analysis also has applications in engineering fields such as nuclear, aerospace, mechanical and electrical engineering.

As a differentiable function of a complex variable is equal to the sum of its Taylor series (that is, it is analytic), complex analysis is particularly concerned with analytic functions of a complex variable (that is, holomorphic functions).

Plot of the function f(x) = (x2 − 1)(x + 2 − i)2 / (x2 + 2 – 2i). The hue represents the function argument, while the brightness represents the magnitude.

History

Complex analysis is one of the classical branches in mathematics, with roots in the 19th century and just prior. Important mathematicians associated with complex analysis include Euler, Gauss, Riemann, Cauchy, Weierstrass, and many more in the 20th century. Complex analysis, in particular the theory of conformal mappings, has many physical applications and is also used throughout analytic number theory. In modern times, it has become very popular through a new boost from complex dynamics and the pictures of fractals produced by iterating holomorphic functions. Another important application of complex analysis is in string theory which studies conformal invariants in quantum field theory.

The Mandelbrot set, a fractal.

Holomorphic functions

Main article: Holomorphic function

Holomorphic functions are complex functions, defined on an open subset of the complex plane, that are differentiable. In the context of complex analysis, the derivative of  f at  z_{0} is defined to be

{\displaystyle f'(z_{0})=\lim _{z\to z_{0}}{\frac {f(z)-f(z_{0})}{z-z_{0}}},z\in \mathbb {C} }.

Although superficially similar to the derivative of a real function, the behavior of complex derivatives and differentiable functions is significantly different. In particular, for this limit to exist, the value of the difference quotient must approach the same complex number, regardless of the manner in which we approach  z_{0} in the complex plane. Consequently, complex differentiability has much stronger consequences than usual (real) differentiability. For instance, holomorphic functions are infinitely differentiable, whereas most real differentiable functions are not. Furthermore, all holomorphic functions satisfy the stronger condition of analyticity, meaning that the function is, at every point in its domain, locally given by a convergent power series. In essence, this means that holomorphic functions can be approximated arbitrarily well by polynomials in some neighborhood of every point in its domain. This stands in sharp contrast to differentiable real functions; even infinitely differentiable real functions can be nowhere analytic.

Most elementary functions, including the exponential function, the trigonometric functions, and all polynomial functions, extended appropriately to complex arguments as functions  {\displaystyle \mathbb {C} \to \mathbb {C} }, are holomorphic over the entire complex plane, making them entire functions, while rational functions  p/q, where p and q are polynomials, are holomorphic on domains that exclude points where q is zero. Such functions that are holomorphic everywhere except a set of isolated points are known as meromorphic functions. On the other hand, the functions  {\displaystyle z\mapsto \Re (z)},  {\displaystyle z\mapsto |z|}, and  {\displaystyle z\mapsto {\bar {z}}} are not holomorphic anywhere on the complex plane, as can be shown by their failure to satisfy the Cauchy-Riemann conditions (see below).

An important property that characterizes holomorphic functions is the relationship between the partial derivatives of their real and imaginary components, known as the Cauchy-Riemann conditions. If  {\displaystyle f:\mathbb {C} \to \mathbb {C} }, defined by{\displaystyle f(z)=f(x+iy)=u(x,y)+iv(x,y)}, where {\displaystyle x,y,u(x,y),v(x,y)\in \mathbb {R} }, is holomorphic on a region  \Omega , then  {\displaystyle (\partial f/\partial {\bar {z}})(z_{0})=0} must hold for all  {\displaystyle z_{0}\in \Omega }. Here, the differential operator  {\displaystyle \partial /\partial {\bar {z}}} is defined as {\displaystyle (1/2)(\partial /\partial x+i\partial /\partial y)}. In terms of the real and imaginary parts of the function, u and v, this is equivalent to the pair of equations  {\displaystyle u_{x}=v_{y}} and {\displaystyle u_{y}=-v_{x}}, where the subscripts indicate partial differentiation. However, it is important to note that functions satisfying the Cauchy-Riemann conditions are not necessarily holomorphic, unless additional continuity conditions are met (see Looman-Menchoff Theorem for a discussion).

Holomorphic functions exhibit some remarkable features. For instance, Picard’s theorem asserts that the range of an entire function can only take three possible forms:  \mathbb {C} ,  {\displaystyle \mathbb {C} \setminus \{z_{0}\}}, or  {\displaystyle \{z_{0}\}} for some z_{0}\in {\mathbb {C}}. In other words, if two distinct complex numbers  z and  w are not in the range of entire function  f, then f is a constant function. Moreover, given a holomorphic function f defined on an open set  U, the analytical extension of f to a larger open set  {\displaystyle V\supset U} is unique. Thus, the value of a holomorphic function over a relatively small region in fact determines the value of the function everywhere to which it can be extended.

 

然既無法長篇大論，只好邀請讀者自己閱讀吧！！

LECTURE NOTES OF WILLIAM CHEN

INTRODUCTION TO COMPLEX ANALYSIS

This set of notes has been organized in such a way to create a single volume suitable for an introduction to some of the basic ideas in complex analysis. The material in Chapters 1 – 11 and 16 were used in various forms between 1981 and 1990 by the author at Imperial College, University of London. Chapters 12 – 15 were added in Sydney in 1996.

To read the notes, click the links below for connection to the appropriate PDF files.

The material is available free to all individuals, on the understanding that it is not to be used for financial gain, and may be downloaded and/or photocopied, with or without permission from the author. However, the documents may not be kept on any information storage and retrieval system without permission from the author, unless such system is not accessible to any individuals other than its owners.