一個小小實驗︰辨識『印刷』的阿拉伯數字

 

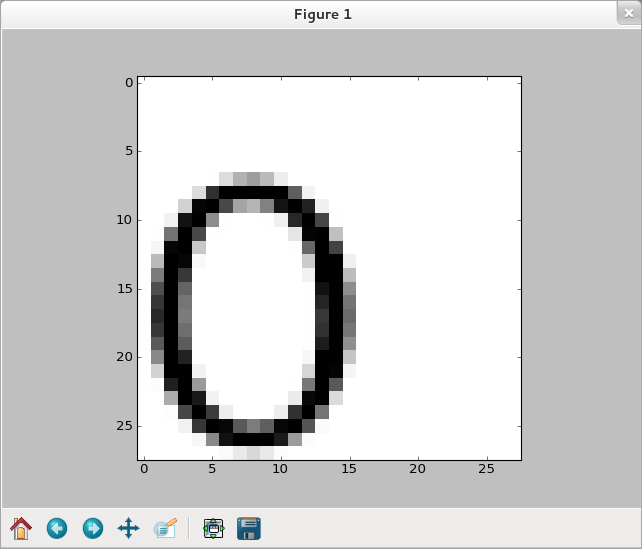
，竟然『network.py』會誤以為是『3』！！難道說『印刷』字能比『手寫』更難辨認的嗎？？或許答案就落在那個『0』是有『位移』的吧？？而那個小程式之『訓練』時用之『手寫數字』資料庫可都是計算過『圖心』的哩！！

THE MNIST DATABASE
of handwritten digits
Yann LeCun, Courant Institute, NYU
Corinna Cortes, Google Labs, New York
Christopher J.C. Burges, Microsoft Research, Redmond

……

The original black and white (bilevel) images from NIST were size normalized to fit in a 20×20 pixel box while preserving their aspect ratio. The resulting images contain grey levels as a result of the anti-aliasing technique used by the normalization algorithm. the images were centered in a 28×28 image by computing the center of mass of the pixels, and translating the image so as to position this point at the center of the 28×28 field.

───

因此『訓練』的『條件』以及『環境』也就決定了『network.py』所擅長之『辨識零點』的了！！？？如是看來人類的『視覺』當真是厲害得很也！！否則如何能作『幾何論證』乎？？豈能發現『九點圓』的呢？？！！

─── 《W!o+ 的《小伶鼬工坊演義》︰神經網絡【MNIST】八》

 

為什麼有『位移』難以辨認？自然也用『平移』產生『視差』呢？

假設人類沒有『雙眼視覺』︰

Binocular vision

Binocular vision is vision in which creatures having two eyes use them together. The word binocular comes from two Latin roots, bini for double, and oculus for eye.^[1] According to Fahle (1987),^[2] having two eyes confers six advantages over having one.

1. It gives a creature a spare eye in case one is damaged.
2. It gives a wider field of view. For example, humans have a maximum horizontal field of view of approximately 190 degrees with two eyes, approximately 120 degrees of which makes up the binocular field of view (seen by both eyes) flanked by two uniocular fields (seen by only one eye) of approximately 40 degrees.^[3]
3. It can give stereopsis in which binocular disparity (or parallax) provided by the two eyes’ different positions on the head gives precise depth perception. This also allows a creature to break the camouflage of another creature.
4. It allows the angles of the eyes’ lines of sight, relative to each other (vergence), and those lines relative to a particular object (gaze angle) to be determined from the images in the two eyes.^[4] These properties are necessary for the third advantage.
5. It allows a creature to see more of, or all of, an object behind an obstacle. This advantage was pointed out by Leonardo da Vinci, who noted that a vertical column closer to the eyes than an object at which a creature is looking might block some of the object from the left eye but that part of the object might be visible to the right eye.
6. It gives binocular summation in which the ability to detect faint objects is enhanced.^[5]
7. It helps see and analyze 3 dimensional objects which are the ones having depth.

Other phenomena of binocular vision include utrocular discrimination (the ability to tell which of two eyes has been stimulated by light),^[6] eye dominance (the habit of using one eye when aiming something, even if both eyes are open),^[7] allelotropia (the averaging of the visual direction of objects viewed by each eye when both eyes are open),^[8] binocular fusion or singleness of vision (seeing one object with both eyes despite each eye’s having its own image of the object),^[9] and binocular rivalry (seeing one eye’s image alternating randomly with the other when each eye views images that are so different they cannot be fused).^[10]

Binocular vision helps with performance skills such as catching, grasping, and locomotion.^[11] It also allows humans to walk over and around obstacles at greater speed and with more assurance.^[12] Optometrists and/or Orthoptists are eyecare professionals who fix binocular vision problems.

Principle of binocular vision with horopter shown

世間會發明『立體眼鏡』

Stereoscope

A stereoscope is a device for viewing a stereoscopic pair of separate images, depicting left-eye and right-eye views of the same scene, as a single three-dimensional image.

A typical stereoscope provides each eye with a lens that makes the image seen through it appear larger and more distant and usually also shifts its apparent horizontal position, so that for a person with normal binocular depth perception the edges of the two images seemingly fuse into one “stereo window”. In current practice, the images are prepared so that the scene appears to be beyond this virtual window, through which objects are sometimes allowed to protrude, but this was not always the custom. A divider or other view-limiting feature is usually provided to prevent each eye from being distracted by also seeing the image intended for the other eye.

Most people can, with practice and some effort, view stereoscopic image pairs in 3D without the aid of a stereoscope, but the physiological depth cues resulting from the unnatural combination of eye convergence and focus required will be unlike those experienced when actually viewing the scene in reality, making an accurate simulation of the natural viewing experience impossible and tending to cause eye strain and fatigue.

Although more recent devices such as Realist-format 3D slide viewers and the View-Master are also stereoscopes, the word is now most commonly associated with viewers designed for the standard-format stereo cards that enjoyed several waves of popularity from the 1850s to the 1930s as a home entertainment medium.

Devices such as polarized, anaglyph and shutter glasses which are used to view two actually superimposed or intermingled images, rather than two physically separate images, are not categorized as stereoscopes.

Old Zeiss pocket stereoscope with original test image

Principles

A simple stereoscope is limited in the size of the image that may be used. A more complex stereoscope uses a pair of horizontal periscope-like devices, allowing the use of larger images that can present more detailed information in a wider field of view. The stereoscope is essentially an instrument in which two photographs of the same object, taken from slightly different angles, are simultaneously presented, one to each eye. This recreates the way which in natural vision, each eye is seeing the object from a slightly different angle, since they are separated by several inches, which is what gives humans natural depth perception. Each picture is focused by a separate lens, and by showing each eye a photograph taken several inches apart from each other and focused on the same point, it recreates the natural effect of seeing things in three dimensions.

A moving image extension of the stereoscope has a large vertically mounted drum containing a wheel upon which are mounted a series of stereographic cards which form a moving picture. The cards are restrained by a gate and when sufficient force is available to bend the card it slips past the gate and into view, obscuring the preceding picture. These coin-enabled devices were found in arcades in the late 19th and early 20th century and were operated by the viewer using a hand crank. These devices can still be seen and operated in some museums specializing in arcade equipment.

The stereoscope offers several advantages:

• Using positive curvature (magnifying) lenses, the focus point of the image is changed from its short distance (about 30 to 40 cm) to a virtual distance at infinity. This allows the focus of the eyes to be consistent with the parallel lines of sight, greatly reducing eye strain.
• The card image is magnified, offering a wider field of view and the ability to examine the detail of the photograph.
• The viewer provides a partition between the images, avoiding a potential distraction to the user.

A stereo transparency viewer is a type of stereoscope that offers similar advantages, e.g. the View-Master

Disadvantages of stereo cards, slides or any other hard copy or print are that the two images are likely to receive differing wear, scratches and other decay. This results in stereo artifacts when the images are viewed. These artifacts compete in the mind resulting in a distraction from the 3d effect, eye strain and headaches.

想拍照『視差』

Parallax

Parallax is a displacement or difference in the apparent position of an object viewed along two different lines of sight, and is measured by the angle or semi-angle of inclination between those two lines.^[1][2] The term is derived from the Greek word παράλλαξις (parallaxis), meaning “alternation”. Due to foreshortening, nearby objects have a larger parallax than more distant objects when observed from different positions, so parallax can be used to determine distances.

To measure large distances, such as the distance of a planet or a star from the earth, astronomers use the principle of parallax. Here, the term “parallax” is the semi-angle of inclination between two sight-lines to the star, as observed when the Earth is on opposite sides of the Sun in its orbit.^[3] These distances form the lowest rung of what is called “the cosmic distance ladder“, the first in a succession of methods by which astronomers determine the distances to celestial objects, serving as a basis for other distance measurements in astronomy forming the higher rungs of the ladder.

Parallax also affects optical instruments such as rifle scopes, binoculars, microscopes, and twin-lens reflex cameras that view objects from slightly different angles. Many animals, including humans, have two eyes with overlapping visual fields that use parallax to gain depth perception; this process is known as stereopsis. In computer vision the effect is used for computer stereo vision, and there is a device called a parallax rangefinder that uses it to find range, and in some variations also altitude to a target.

A simple everyday example of parallax can be seen in the dashboard of motor vehicles that use a needle-style speedometer gauge. When viewed from directly in front, the speed may show exactly 60; but when viewed from the passenger seat the needle may appear to show a slightly different speed, due to the angle of viewing.

A simplified illustration of the parallax of an object against a distant background due to a perspective shift. When viewed from “Viewpoint A”, the object appears to be in front of the blue square. When the viewpoint is changed to “Viewpoint B”, the object appears to have moved in front of the red square.

This animation is an example of parallax. As the viewpoint moves side to side, the objects in the distance appear to move more slowly than the objects close to the camera.

照片嗎？

─── 摘自《GoPiGo 小汽車︰格點圖像算術《色彩空間》時中︰立體視覺【一】》

 

此乃『單眼』小汽車煩惱如何得『立體視覺』也！就像『平面國』的科學家思考怎麼樣『定位一點』矣！！

※ 註︰ 新版 raspbian stretch 測試。

pi@raspberrypi:~  geogebra

參考文本︰

 

然而所必須『邏輯』一致者，終究落於『假設』乎？？！！

白露起秋意，早晚催知了。知了有五眼！晨昏聲聲報？

將如何看待『正則式』耶？

Normal form

Möbius transformations are also sometimes written in terms of their fixed points in so-called normal form. We first treat the non-parabolic case, for which there are two distinct fixed points.

Non-parabolic case:

Every non-parabolic transformation is conjugate to a dilation/rotation, i.e. a transformation of the form

 

(k ∈ C) with fixed points at 0 and ∞. To see this define a map

 

which sends the points (γ₁, γ₂) to (0, ∞). Here we assume that γ₁ and γ₂ are distinct and finite. If one of them is already at infinity then g can be modified so as to fix infinity and send the other point to 0.

If f has distinct fixed points (γ₁, γ₂) then the transformation  has fixed points at 0 and ∞ and is therefore a dilation: . The fixed point equation for the transformation f can then be written

 

Solving for f gives (in matrix form):

or, if one of the fixed points is at infinity:

From the above expressions one can calculate the derivatives of f at the fixed points:

and 

Observe that, given an ordering of the fixed points, we can distinguish one of the multipliers (k) of f as the characteristic constant of f. Reversing the order of the fixed points is equivalent to taking the inverse multiplier for the characteristic constant:

For loxodromic transformations, whenever |k| > 1, one says that γ₁ is the repulsive fixed point, and γ₂ is the attractive fixed point. For |k| < 1, the roles are reversed.

Parabolic case:

In the parabolic case there is only one fixed point γ. The transformation sending that point to ∞ is

or the identity if γ is already at infinity. The transformation  fixes infinity and is therefore a translation:

Here, β is called the translation length. The fixed point formula for a parabolic transformation is then

Solving for f (in matrix form) gives

or, if γ = ∞:

Note that β is not the characteristic constant of f, which is always 1 for a parabolic transformation. From the above expressions one can calculate:

 

─── 摘自《GoPiGo 小汽車︰格點圖像算術《投影幾何》【五‧線性代數】《導引七‧變換組合 VII‧B 》》

 

故不得不思辨『變換』前、後耶！！？？