每日彙整: 2017-09-16

樹莓派、樹莓派之學習、樹莓派之教育

GoPiGo 小汽車︰格點圖像算術《投影幾何》【五‧線性代數】《導引七‧變換組合 VIII‧⚃ 》

史記‧卷八十一‧廉頗藺相如列傳‧第二十一

奢子‧括

趙括自少時學兵法，言兵事，以天下莫能當。嘗與其父奢言兵事，奢不能難，然不謂善。括母問奢其故，奢曰：「兵，死地也，而括易言之。使趙不將括即已，若必將之，破趙軍者必括也。」及括將行，其母上書言於王曰：「括不可使將。」王曰：「何以？」對曰 ：「始妾事其父，時為將，身所奉飯飲而進食者以十數，所友者以百數，大王及宗室所賞賜者盡以予軍吏士大夫，受命之日，不問家事。今括一旦為將，東向而朝，軍吏無敢仰視之者，王所賜金帛 ，歸藏於家，而日視便利田宅可買者買之。王以為何如其父？父子異心，原王勿遣。」王曰：「母置之，吾已決矣。」括母因曰：「王終遣之，即有如不稱，妾得無隨坐乎？」王許諾。

趙括既代廉頗，悉更約束，易置軍吏。秦將白起聞之，縱奇兵，詳敗走，而絕其糧道，分斷其軍為二，士卒離心。四十餘日，軍餓，趙括出銳卒自博戰，秦軍射殺趙括。括軍敗，數十萬之眾遂降秦，秦悉阬之。趙前後所亡凡四十五萬。明年，秦兵遂圍邯鄲，歲餘，幾不得脫。賴楚、魏諸侯來救，乃得解邯鄲之圍。趙王亦以括母先言，竟不誅也。

 

若說古之『紙上談兵』曾引發遺憾！誠始於缺乏身『體』實『驗』也？今已有『虛擬』、『擴增』種種 … 實境之科技，當無有疑慮的乎？

此處且借下圖

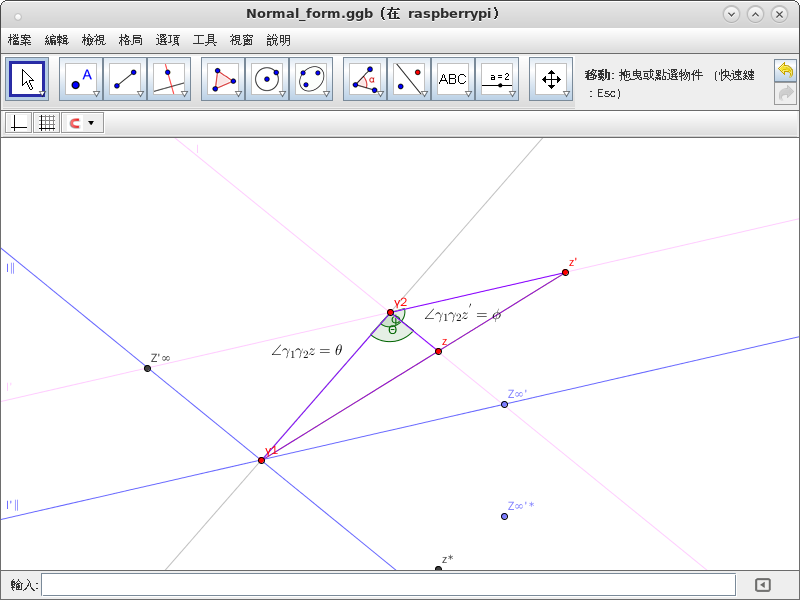
依上圖，三角形 \Delta {\gamma}_1 {\gamma}_2} z^{'} 與 \Delta {\gamma}_1 {\gamma}_2} z 面積比可以兩算︰

‧ 以 z-{\gamma}_1} 和 z^{'}-{\gamma}_1} 為底 = \frac{z^{'} - {\gamma}_1}{z - {\gamma}_1}} ；

‧ 以 z-{\gamma}_2} 和 z^{'}-{\gamma}_2}  為底

= \frac{|{\gamma}_1 {\gamma}_2| \cdot \sin(\angle \phi)}{|{\gamma}_1 {\gamma}_2| \cdot \sin(\angle \theta)} \cdot \frac{z^{'} - {\gamma}_2}{z - {\gamma}_2}} = k \cdot \frac{z^{'} - {\gamma}_2}{z - {\gamma}_2}}

\therefore k = \frac{ \sin(\angle \phi)}{ \sin(\angle \theta)}

既『角不變』，『角比』能變嗎★

故而 \frac{z^{'} - {\gamma}_1}{z - {\gamma}_1}} = k \cdot \frac{z^{'} - {\gamma}_2}{z - {\gamma}_2}} ，

且將兩邊乘上 \frac{z - {\gamma}_1}{z^{'} - {\gamma}_2}

果非所求的嘛☆

 

談談邏輯是否能蘊涵  □ ○ \Rightarrow 耶！

‧從上圖可知 \overline{{\gamma}_1z_{{\infty}^{'}}} 和 \overline{ {\gamma}_1 {\gamma}_2} 相交於 {\gamma}_1  也，卻不能知是否具有其它等等 … 『性質』矣。

‧ 因不知『原點』 O 在何處，故無法確定 O, {\gamma}_1, {\gamma}_2 是否在一線上 ？

於是就算明白 k 是『角比』，少了 z_{{\infty}^{'}} 確定 l, l^{'} 兩線定位，疑惑恐生焉？！

因此若祇考之以

※ 註 - z_{{\infty}^{'}} = \frac{k {\gamma}_1 - {\gamma}_2}{1-k}

豈非 z_{{\infty}^{'}} = \frac{-k {\gamma}_1 + {\gamma}_2}{1-k} = (1 - \frac{1}{1-k}}) {\gamma}_1 + \frac{1}{1-k}}{\gamma}_2 ，

座落在 \overline{{\gamma}_1 {\gamma}_2} 線上嗎？那又怎麼可能的呢！？

此時如果回顧反觀︰

且再舉『透視』的『特徵平行四邊形』 p Z_{{\infty}^{'}} Z_x {Z^{'}}_{\infty} 推導為例︰

上圖假設『透視中心』 p 是『原點』，

\therefore z_{\Box}^{\bigcirc} - p = z_{\Box}^{\bigcirc} - 0 = z_{\Box}^{\bigcirc} 。

如果用 z^{'} = P(z) 表示這個『透視函數』，那麼

P(Z_x) = Z_x

P(\infty) = {Z^{'}}_{\infty}

 \infty = P(Z_{{\infty}^{'}}) 。

幾何意指

‧ Z_x 是 l 、l^{'} 兩線交點。

‧ Z_{{\infty}^{'}} \ \parallel \ l^{'}

‧ {Z^{'}}_{\infty} \ \parallel \ l 。

因三角形 \Delta p Z_{{\infty}^{'}} z 和 \Delta z' Z_x z 相似，故

\frac{z^{'}-z}{z} = \frac{Z_x - z}{z - Z_{{\infty}^{'}}}

左右兩邊加一自得

\Rightarrow \frac{z^{'}}{z} = \frac{(Z_x - z) + (z - Z_{{\infty}^{'}})} {z - Z_{{\infty}^{'}}} = \frac{Z_x - Z_{{\infty}^{'}}} {z - Z_{{\infty}^{'}}} = \frac{{{Z^{'}}_{\infty}}}{z - Z_{{\infty}^{'}}} 哩◎

假使 p 不是『原點』，可得

z^{'} - p = \frac{({{Z^{'}}_{\infty}} - p)(z-p)}{(z-p) - (Z_{{\infty}^{'}} - p)}

\Rightarrow z^{'} = \frac{{{Z^{'}}_{\infty}} z \ - \ p({{Z^{'}}_{\infty}} + Z_{{\infty}^{'}} - p)}{z - Z_{{\infty}^{'}}} = \frac{{{Z^{'}}_{\infty}} z \ - \ p \cdot Z_x}{z - Z_{{\infty}^{'}}}

可 知它的兩個『定點』 z^{'} = z 就是 p 和 Z_x ，而且 p + Z_x = {{Z^{'}}_{\infty}} + Z_{{\infty}^{'}}, \ \because Z_x - p = ({{Z^{'}}_{\infty}} -p) + (Z_{{\infty}^{'}}-p)

─── 摘自《GoPiGo 小汽車︰格點圖像算術《投影幾何》【五‧線性代數】《導引七‧變換組合 VII‧A 》》

 

文義當是 \overline{{\gamma}_1 z_{{\infty}^{'}}} \parallel l^{'} 乎？所以 \overline{z_{{\infty}^{'}} - {\gamma}_1}} = |\frac{1}{1-k}| \cdot \overline{{\gamma}_2 - {\gamma}_1} 耶？？

何況已知 \frac{z^{'} - {\gamma}_1}{z^{'} - {\gamma}_2} = k \cdot \frac{z - {\gamma}_1}{z - {\gamma}_2} 。可得

\lim \limits_{z \to z_{{\infty}^{'}}} \frac{z^{'} - {\gamma}_1}{z^{'} - {\gamma}_2} = \lim \limits_{z^{'} \to \infty} \frac{z^{'} - {\gamma}_1}{z^{'} - {\gamma}_2} = 1

= \lim \limits_{z \to z_{{\infty}^{'}}} k \cdot \frac{z - {\gamma}_1}{z - {\gamma}_2} = k \cdot \frac{z_{{\infty}^{'}} - {\gamma}_1}{z_{{\infty}^{'}} - {\gamma}_2} ，解之正是

z_{{\infty}^{'}} = \frac{-k {\gamma}_1 + {\gamma}_2}{1-k} = (1 - \frac{1}{1-k}}) {\gamma}_1 + \frac{1}{1-k}}{\gamma}_2 的哩！

符號之用、意義之定，深也哉◎