每日彙整: 2017-09-07

樹莓派、樹莓派之學習、樹莓派之教育

GoPiGo 小汽車︰格點圖像算術《投影幾何》【五‧線性代數】《導引七‧變換組合 VI‧XI 》

三十六計‧聲東擊西

敵志亂萃，不虞。

坤下兑上之象，利其不自主而取之。

 

『萃』聚也。

易經‧第四十五卦‧澤地萃 ䷬

萃：亨。 王假有廟，利見大人，亨，利貞。 用大牲吉，利有攸往。

彖曰：萃，聚也﹔順以說，剛中而應，故聚也。王假有廟，致孝享也。利見大人亨，聚以正也。 用大牲吉，利有攸往，順天命也。 觀其所聚，而天地萬物之情可見矣。

象曰：澤上於地，萃﹔君子以除戎器，戒不虞。

『亂萃』散沙矣。『虞』如『智者千慮』，『不虞』似『意料之外 』耶？故而集思廣益，盼望眾志成城乎！

假使說用『齊次座標』

\left( \begin{array}{ccc} x^{'} \\ y^{'} \\ 1 \end{array} \right) = \left( \begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \end{array} \right) \left( \begin{array}{ccc} x \\ y \\ 1 \end{array} \right)

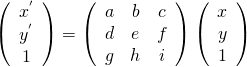
表達『投影面』順理成章。因為

透視投影

透視投影是為了獲得接近真實三維物體的視覺效果而在二維的紙或者畫布平面上繪圖或者渲染的一種方法，它也稱為透視圖。透視投影的繪製必須根據已有的幾何規則進行。

 

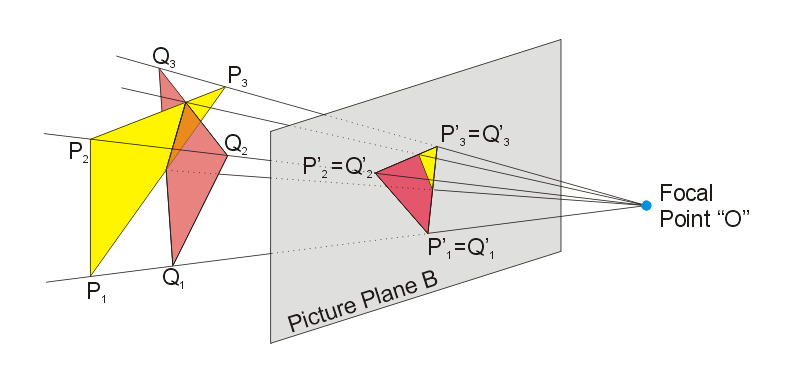
之『投影面』上的『投影點』 ── 過 O 視線與投影面之交點 ── ，『投影線』 ── 過 O 視面與投影面之交線 ── ，和三維空間裡的『點』、『線』、『面』關係對當，所以直覺自然生焉！？

倘問是否能用『投影面』處理『投影線』呢？？豈有『三維』不能料理『二維』的呀！！祇怕不只是殺雞用牛刀，還別講那也不容易的呦！！？？

如果『設問之詞』宛若『聲東擊西』︰前一篇

問題是

\left( \begin{array}{cc} z^{'} \\ 1 \end{array} \right) = \left( \begin{array}{cc} a & b \\ c & d \end{array} \right) \left( \begin{array}{cc} z \\ 1 \end{array} \right)

有道理嗎☆

寓言歷時斷續的『學習』將如何談其『聚』『散』之道勒？？！！

回顧『平面國』︰

就像追問『點投派』者有疑焉︰

假使 P 是『點投派』一『投影函數』，滿足

P \left( \begin{array}{cc} x \\ y \end{array} \right) = \left( \begin{array}{cc} x/y \\ 1 \end{array} \right)

且  P^2 = P 後，

劍指

A := \left( \begin{array}{cc} a & b \\ c & d \end{array} \right)

之罔然也︰

Basic definitions

Definition 1.1   The is the set of all lines in passing through the origin.

Note that if and are two nonzero vectors lying on the same line through the origin, then they are multiples of each other. This remark allows us to redefine as the quotient of by the equivalence relation (or ) if and are multiples of each other.

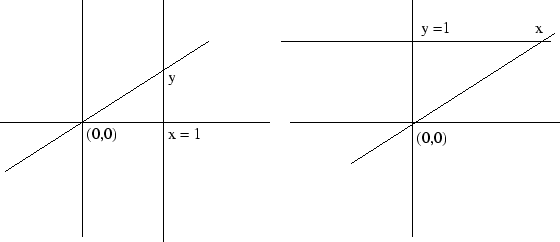
Exercise 1.6 (00)   Let be the slope of the line passing through the origin and let

be an invertible matrix. Verify that the slope of the line equals .

This exercise tells us that in suitable coordinates projective transformations have the form .

As explained in [2], projective geometry arose from the artists’ needs to represent the three-dimensional world on a two-dimensional canvas. An artist in Flatland just has to worry about representing a two-dimensional world on a one-dimensional canvas. The figure below shows a Flatland artist copying a one-dimensional image onto a canvas. Notice how distances are distorted.

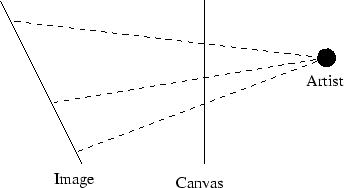
This type of correspondence between the points in two lines is called a perspective.

─ 摘自《GoPiGo 小汽車︰格點圖像算術《投影幾何》【三下】》

 

因為依據『行列式性質』︰

……

遵循『逆矩陣規矩』︰

………

豈能不是

A^{-1} \cdot A^2 = A^{-1} \cdot A = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right)

哩◎

─── 摘自《GoPiGo 小汽車︰格點圖像算術《投影幾何》【四‧平面國】《丙》》

 

重溫『賦值史』︰

且讓我們將『單點透視』放在以『投影中心』 P 為『齊次座標』之『原點』的平面上作考察︰

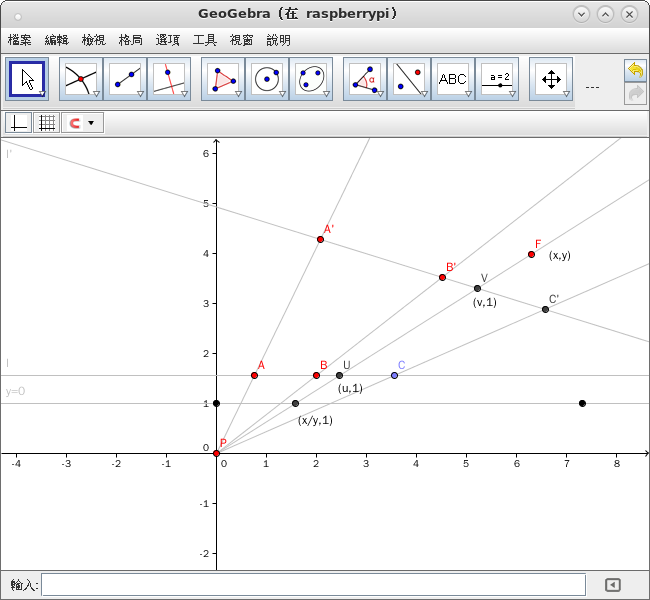
如果依舊選用『本地座標系』︰

A \ {\overset {P}{\doublebarwedge }} \ A^{'} ， B \ {\overset {P}{\doublebarwedge }} \ B^{'} ， C \ {\overset {P}{\doublebarwedge }} \ C^{'}

\overline{AB} 是線 l 上的『單位長度』，任意一點 C 之『賦值』為 t = \frac{\overline{CA}}{\overline{CB}} = \frac{u}{u -1}, \ u =_{df} \frac{\overline{CA}}{\overline{AB}} 。對應之

\overline{A^{'}B{'}} 是線 l^{'} 上的『單位長度』，任意一點 C^{'} 之『賦值』為 t^{'} = \frac{\overline{C^{'}A^{'}}}{\overline{C^{'}B^{'}}} = \frac{v}{v -1}, \ v =_{df} \frac{\overline{C^{'}A^{'}}}{\overline{A^{'}B^{'}}}

l 與 l^{'} 間的『幾何事實』仍然是

\frac{\frac{\overline{CA}}{\overline{CB}}}{\frac{\overline{C^{'}A^{'}}}{\overline{C^{'}B{'}}} } = \frac{\frac{\overline{PA}}{\overline{PB}}}{\frac{\overline{PA^{'}}}{\overline{PB^{'}}}} = constant = \frac{1}{k} = \frac{t}{t^{'}} 。

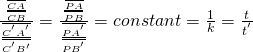因此『透視』間之『數值關係』還是︰

f_P ={\begin{cases} k \cdot t,&{\mbox{if }} U \in l \\ \frac{t^{'}}{k} ,&{\mbox{if }} V \in l^{'} \end{cases} 。

f_P ={\begin{cases} \frac{u}{(1- \frac{1}{k}) u + \frac{1}{k}},&{\mbox{if }} U \in l \\ \frac{v}{(1-k)v +k} ,&{\mbox{if }} V \in l^{'} \end{cases} 。

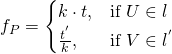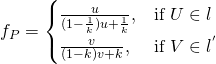若說使用這麼麻煩的『記號法』，祇為著講『兩線間之透視』，其『點與點』間『函數』，滿足『對射定義』︰

……

乾脆說『反演』存在吧！！

t, t^{'} 容易計算

f_P(f_P(C)) \equiv f_P(C^{'}) = f_P(k \cdot t) = \frac{1}{k} \cdot (k \cdot t) = t \equiv C ，

u, v 需要化簡

f_P(f_P(u)) = u 。

………

如是按『語意約定』，或可簡化為︰

\left( \begin{array}{cc} v \\ 1 \end{array} \right) = \ \left( \begin{array}{cc} \frac{u}{(1- \frac{1}{k}) u + \frac{1}{k}} \\ 1 \end{array} \right) \ {\overset {P}{\doublebarwedge }} \ \left( \begin{array}{cc} 1 & 0 \\ 1 - \frac{1}{k} & \frac{1}{k} \end{array} \right) \left( \begin{array}{cc} u \\ 1 \end{array} \right) ；

\left( \begin{array}{cc} u \\ 1 \end{array} \right) = \ \left( \begin{array}{cc} \frac{v}{(1- k) v + k} \\ 1 \end{array} \right) \ {\overset {P}{\doublebarwedge }} \ { \left( \begin{array}{cc} 1 & 0 \\ 1 - \frac{1}{k} & \frac{1}{k} \end{array} \right)}^{-1} \left( \begin{array}{cc} v \\ 1 \end{array} \right)

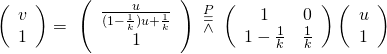{\overset {P}{\doublebarwedge }} \ \left( \begin{array}{cc} 1 & 0 \\ 1 - k & k \end{array} \right) \left( \begin{array}{cc} v \\ 1 \end{array} \right) 的乎？？！！

─── 摘自《GoPiGo 小汽車︰格點圖像算術《投影幾何》【五‧線性代數】《導引六‧上》》

 

且再請讀者體會『複數』 ─ 『二元』 (x, y) = x + y * i 的『數』 ─ 之神奇。因其『二元』故可代表平面上的『任一點』；又能求『倒數』 \frac{1}{z} = \frac{z^{*}}{z z^{*}} ；實恰通『投影線透視』之奧妙也◎