如果讀一本『代數幾何』,其中有一段文字這麼寫︰
設有 ![]() 兩線,而且
兩線,而且 ![]() 與
與 ![]() 是那兩線上共線和對應之三點。已知
是那兩線上共線和對應之三點。已知 ![]() ,那麼這兩線之間形成透視關係,同時滿足『分式線性變換』形式。
,那麼這兩線之間形成透視關係,同時滿足『分式線性變換』形式。
假使此時方嘗試『辨名識物』中英『廣徵博引』︰
Linear fractional transformation
In mathematics, the phrase linear fractional transformation usually refers to a Möbius transformation, which is a homography on the complex projective line P(C) where C is the field of complex numbers.
More generally in mathematics, C may be replaced by another ring (A, +, ×).[1] For example, the Cayley transform is a linear fractional transformation originally defined on the 3 x 3 real matrix ring.
In general, a linear fractional transformation refers to a homography over P(A), the projective line over a ring. When A is a commutative ring, then the linear fractional transformation has the familiar form
Otherwise homographies are expressed (az + b, cz + d) with homogeneous coordinates. The equivalence of such coordinates is expressed
莫比烏斯變換
在幾何學裡, 莫比烏斯變換是一類從黎曼球面映射到自身的函數。用擴展複平面上的複數表示的話,其形式為:
其中 z, a, b, c, d 為滿足 ad − bc ≠ 0的(擴展)複數。
莫比烏斯變換也可以被分解為以下幾個變換:把平面射影到球面上,把球體進行旋轉、位移等任何變換,然後把它射影回平面上。 莫比烏斯變換是以數學家奧古斯特·費迪南德·莫比烏斯的名字命名的,它也被叫做單應變換(homographic transformation)或分式線性變換(linear fractional transformation)。
分解與基本性質
莫比烏斯變換的實質與反演密切相關。實際上,一個形如
的莫比烏斯變換可以分解成四個變換[3]:51:
這四個變換的複合就是莫比烏斯變換:
在這種分解之下,我們可以清楚地看出莫比烏斯變換的不少基本性質。首先,由於以上分解中的每個變換都是可逆的(它們的逆變換也十分清楚),因此可以容易地看出,莫比烏斯變換的逆變換也是一個莫比烏斯變換,而且其表達式可以具體計算。具體來說,設變換函數 ,其中每一個
的逆變換(反函數),
那麼莫比烏斯變換f的逆變換就是:
-
[3]:51
保角性與保圓性
由於莫比烏斯變換可以分解為平移、反演、位似與旋轉變換,因此能夠保持所有反演變換的性質。一個基本的例子是保角性:由於平移、反演、位似與旋轉變換都保持角度不變,因此兩個複數(或向量)之間的幅角差(夾角)在經過莫比烏斯變換後不變。
此外,一個廣義圓經 過莫比烏斯變換後,仍會映射到一個廣義圓。廣義圓是指黎曼球面上的圓,包括普通的圓形和帶無窮遠點的直線(可以認為是一個半徑無限大的圓)。這也是反演保 持廣義圓的結果。當然莫比烏斯變換並不是將圓映射到圓,將直線映射到直線,經過映射後直線可能變成圓,圓也可能變成直線。
複比不變性
莫比烏斯變換也可以保持複數的複比不變。設有四個兩兩不同的複數 ,對應擴充複平面上四個不同的點,它們經過莫比烏斯變換後變成
四點,那麼複比:
當 中有一個或多個是無窮大時,複比就定義為相應逼近的極限。比如說當四個複數是
時,複比就是:
確定莫比烏斯變換
給定平面上三個不同點 ,存在著唯一的一個莫比烏斯變換
,使得
分別等於
。這個莫比烏斯變換就是:
而由於對於另外的三個不同點 ,也唯一存在一個莫比烏斯變換
,使得
分別等於
。因此,對於任意一組出發點
,任意一組到達點
,都唯一存在一個莫比烏斯變換,將
分別映射到點
。具體地說,這個變換就是
[3]:59-60。作為推論,如果一個莫比烏斯變換有三個不動點,那麼它是恆等變換。
,總覺得『月朦朧、鳥朦朧』乎??或許該曉『規矩基本』耶!!

傳說魯班造矩先。伏羲手中原何處?大禹果真得洛書?左準繩且右規矩,己身度量稱以出?莫道此事實稽無,丁蘭魯班陰陽度!
【魯班尺】

【丁蘭尺】

吉凶禍福因事起?當真博識可拯難。辨物怎得無之前,益流福好唯一謙!
問世間器物創作又何故耶??!!
─── 摘自《光的世界︰矩陣光學七》
就讓我們順著前頭文字且補一圖往下推演吧︰

依題意
![]() ,
,
![]() 。
。
按條件
![]()
![]()
![]() 。
。
求解 ![]() 可知
可知
![]() ,
,
似乎曾相識哩??
且讓我們將『單點透視』放在以『投影中心』 ![]() 為『齊次座標』之『原點』的平面上作考察︰
為『齊次座標』之『原點』的平面上作考察︰
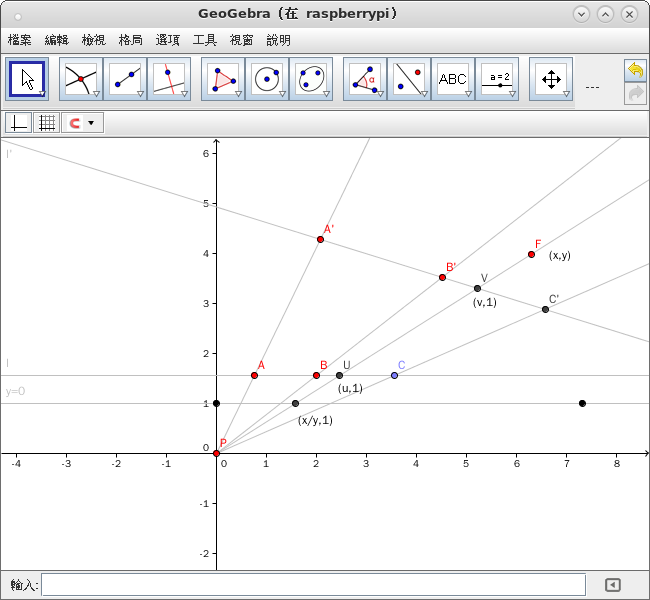
如果依舊選用『本地座標系』︰
![]() ,
, ![]() ,
, ![]()
![]() 是線
是線 ![]() 上的『單位長度』,任意一點
上的『單位長度』,任意一點 ![]() 之『賦值』為
之『賦值』為 ![]()
![]() 。對應之
。對應之
![]() 是線
是線 ![]() 上的『單位長度』,任意一點
上的『單位長度』,任意一點 ![]() 之『賦值』為
之『賦值』為 ![]()
![]()
![]() 與
與 ![]() 間的『幾何事實』仍然是
間的『幾何事實』仍然是
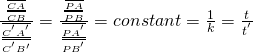 。
。
因此『透視』間之『數值關係』還是︰
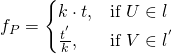 。
。
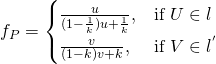 。
。
─── 摘自《GoPiGo 小汽車︰格點圖像算術《投影幾何》【五‧線性代數】《導引六‧上》》
若把
![]() 、
、
![]() ;代入原式
;代入原式
將得 ![]() 呀◎
呀◎





