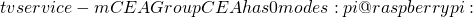承上篇,縱已知 tvservice -m DMT | CEA 回報模式或數值未必可用 ,然其終究也是判定顯示器好壞指標乎?
[1024×600] 之 [640×480]
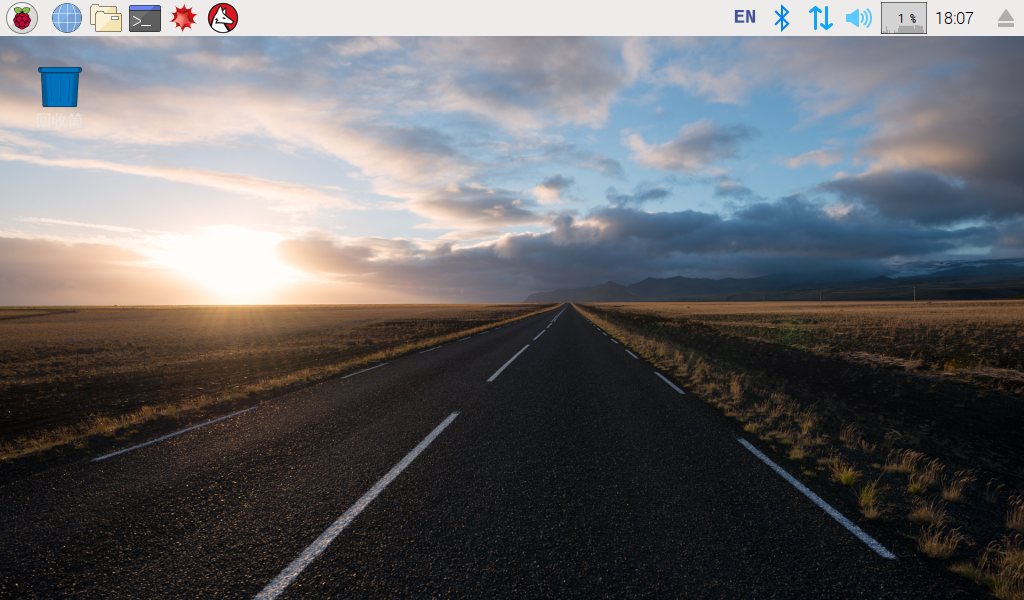
※ 正常開機,進入 X Window 系統。
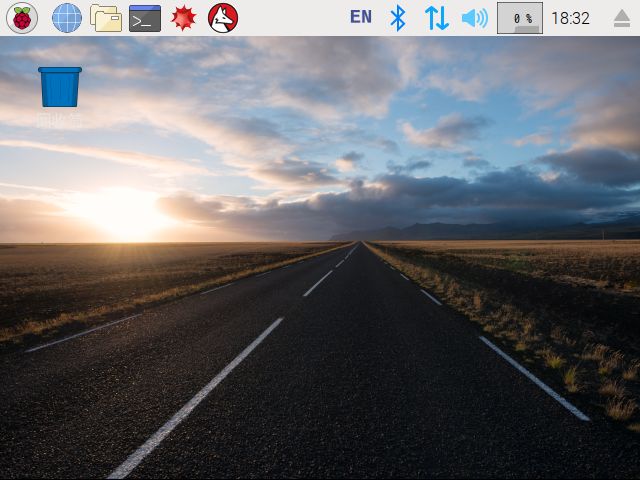
[1280×800] 的 [640×480]
※ 不能開機直接進入 X Window 環境。啟用終端機模式,無法擷取正確畫面,下圖所顯示之兩段式模擬畫面,實處於同一個螢幕也。
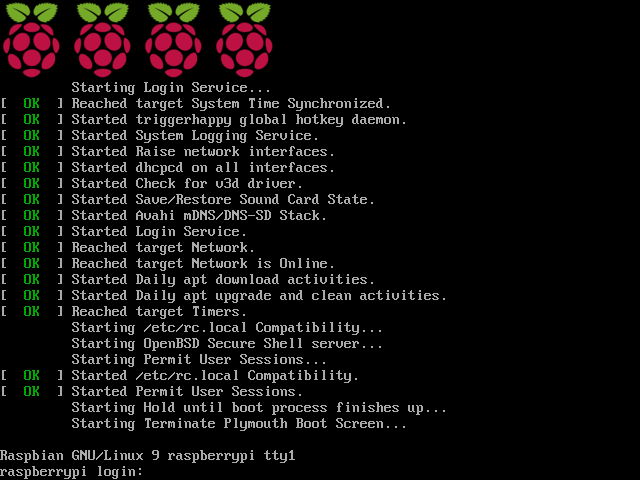

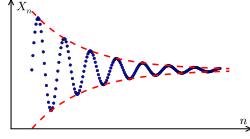
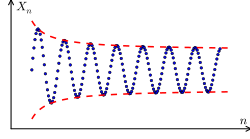
故而假借二分逼近法︰
在《λ 運算︰計物數《上》》一文中,我們說到『皮亞諾』 Peano 提出了『自然數』之五條公設的系統。用著『未定義』的『基元』數『零 0』,以及『後繼數』successor 的『概念』,打造了『一階算術』系統,現今稱之為『皮亞諾算術系統』。在《布林代數》文章裡,我們對比了『布林代數』、『集合論』與『邏輯學』之間的『密切關係』。整個『布林代數』是可以建立在一個二元運算『孤虛』 ── Sheffer豎線 ![]() ── 之上。也就是說一個『系統』的『公設化』往往不只一種『選擇』,或許是因為雖然兩個看起來『不同』的『概念』,它們彼此之間的『邏輯關係』卻是『等價的』,所以『甲可以推導出乙』,而且『乙能夠演繹出甲』,在此處,我們僅以與『無窮小』概念的『親疏遠近』編排次序,並不論及何者更為『基本』這樣的判斷。
── 之上。也就是說一個『系統』的『公設化』往往不只一種『選擇』,或許是因為雖然兩個看起來『不同』的『概念』,它們彼此之間的『邏輯關係』卻是『等價的』,所以『甲可以推導出乙』,而且『乙能夠演繹出甲』,在此處,我們僅以與『無窮小』概念的『親疏遠近』編排次序,並不論及何者更為『基本』這樣的判斷。
『羅素悖論』在『集合論』的發展史上產生了重大的影響,因此『集合之集合』的構造勢必得『避免矛盾』,『坎特爾』 Cantor 證明了『實數集合』的『元素』是『不可數』的多,這再次引發了如何『列舉』的『難題』,也就是說既然『實數』如果無法『一一指定』,那你又怎麽能夠確定『所說之數』是『存在的』呢?比方說 ![]() 。所以我們從『言之有物』的觀點,就直接『同意』所謂的『選擇公理』︰一個【集合族】是指由非『空集合』
。所以我們從『言之有物』的觀點,就直接『同意』所謂的『選擇公理』︰一個【集合族】是指由非『空集合』 ![]() 所組成的一個『集合』。『存在』著一種【選擇函數】,它是個定義在某個『集合族』
所組成的一個『集合』。『存在』著一種【選擇函數】,它是個定義在某個『集合族』 ![]() 上的函數,對於這個函數來講,所有在『集合族』
上的函數,對於這個函數來講,所有在『集合族』 ![]() 中的『集合元素』
中的『集合元素』 ![]() ,都能夠『選擇』
,都能夠『選擇』 ![]() 。也就是說
。也就是說 ![]() 可以『指定』某一個
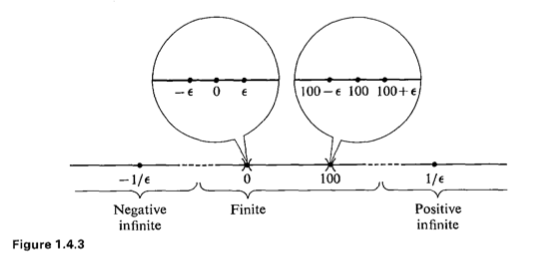
可以『指定』某一個 ![]() 中的『元素』 。這裡所說的『同意』之意思就不過是想要在『直觀』中『簡化』討論之事項,比方講像某些『探討』著一條平面上的『封閉曲線』,它到底是不是能夠將『平面』分割成『曲線內』與『曲線外』之兩個部分的此類『議論』。這樣『實數分析』中所謂的『疊套閉區間』
中的『元素』 。這裡所說的『同意』之意思就不過是想要在『直觀』中『簡化』討論之事項,比方講像某些『探討』著一條平面上的『封閉曲線』,它到底是不是能夠將『平面』分割成『曲線內』與『曲線外』之兩個部分的此類『議論』。這樣『實數分析』中所謂的『疊套閉區間』 ![]()
![]() 的『概念』,就『超實數』
的『概念』,就『超實數』 ![]() 來講,就是『標準部份函數』
來講,就是『標準部份函數』 ![]() ,所以說如果那個
,所以說如果那個 ![]() 的話,一定會有
的話,一定會有 ![]() ,也就是說這就『確定』了那個『實數值』。假使我們換個觀點來看
,也就是說這就『確定』了那個『實數值』。假使我們換個觀點來看 ![]() 與
與 ![]() 都各自構成一個了『單調』之『上升』以及『單調』之『下降』的『序列』,而且
都各自構成一個了『單調』之『上升』以及『單調』之『下降』的『序列』,而且 ![]() ,那麼難到不該
,那麼難到不該 ![]() 的嗎?如果說自然界之『物理量』總是來自於『度量』,因此那兩個稱作『柯西序列』 Cauchy sequence 的
的嗎?如果說自然界之『物理量』總是來自於『度量』,因此那兩個稱作『柯西序列』 Cauchy sequence 的 ![]() 的『序列』,它們所『代表』的就是『量測』的『極限分析』的啊!假使用『超整數』與『巨量』
的『序列』,它們所『代表』的就是『量測』的『極限分析』的啊!假使用『超整數』與『巨量』 ![]() 可敘述為
可敘述為 ![]() 。假使設想著對於『可列舉』之物,至少可以說在『無窮遠』處之時﹐『那些‧哪些』的物將會是距離『這麼‧這麼』之『無窮近』的吧?然而對於『不可列舉』之物,我們真的還能夠講述著『某個‧某個』的『什麼』的嗎?因為說不定它還框陷在『難計』的『侑限』裡,你又怎麽可能得到『遠近』之『結論』的呢??或許這就是『有理數』的『可數性』很適合用來『建構』那種『不可數性』的吧!!
。假使設想著對於『可列舉』之物,至少可以說在『無窮遠』處之時﹐『那些‧哪些』的物將會是距離『這麼‧這麼』之『無窮近』的吧?然而對於『不可列舉』之物,我們真的還能夠講述著『某個‧某個』的『什麼』的嗎?因為說不定它還框陷在『難計』的『侑限』裡,你又怎麽可能得到『遠近』之『結論』的呢??或許這就是『有理數』的『可數性』很適合用來『建構』那種『不可數性』的吧!!
── 摘自《【Sonic π】電路學之補充《四》無窮小算術‧下下‧上》
驗證 raspbian stretch 版本始末,說此恐將失敗,最後成功者耶◎
pi@raspberrypi:~tvservice -m DMT Group DMT has 2 modes: mode 4: 640x480 @ 60Hz 4:3, clock:25MHz progressive (prefer) mode 27: 1280x800 @ 60Hz 16:10, clock:71MHz progressive pi@raspberrypi:~