大哲學家亞里士多德認為自然界有一種『原因』Cause 關係,它用著『因為 Because 』回答了『為什麼』Why 之問題。他列舉了四種原因,故簡稱之為『四因說』︰
任何『事物』是由它所構成的『原料』、『組件』和『元素』,按著一套完整的『架構』、『組裝』與『結合』方式才形成的,這個『材質』的部份,就是『物質因』Material Cause ;而那個架構規劃的『藍圖』就是『形式因』Formal Cause,形式因也定義了『□之所以是□』。其次任何『事物』之『存在』總是有理由的,它因著『目的因』Final Cause 而能在時空中『存有』,又可能將隨著時流因之而被改變,這就推動著『動力因』Efficient Cause 去『改變什麼』?又會『如何將之改變』!!
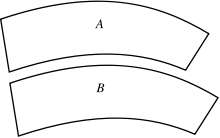
那麼亞里士多德的四因說,能不能解說這個『忒修斯之船』的同一性問題呢?也許先讓我們聽聽孔老夫子的『觚之抱怨』吧!
《倫语‧雍也》:
子曰:觚不觚,觚哉!觚哉!
朱熹集注:觚,棱也;或曰酒器,或曰木簡,皆器之有棱者也。不觚者,蓋當時失其制而不為棱也。觚哉:觚哉!言不得為觚也。
從造字來講,『觚』字也有『棱角』的啊,竟然將『方』觚改為『圓』觚!無怪乎孔老夫子會喊著『這算是個觚嗎』?『這難到也算是個觚嗎』??
因此如果問他老先生這個『忒修斯之船』的問題,也許他會說︰依其『形制』並沒有什麼被『改變』,所以還一樣是『那個』。或許說『形式因』定義著『什麼是什麼』,所以相較之下比它是用『什麼所構成』的『物質因』還來的重要的吧!!
─── 摘自《Thue 之改寫系統《三》》
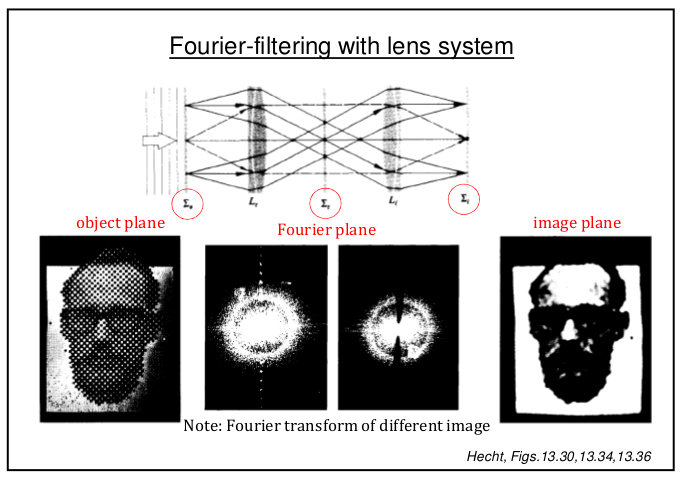
前三篇文本中,我們談了一般『光學矩陣』
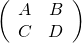
只要 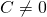 ,都可借著『自由空間』
,都可借著『自由空間』
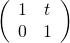
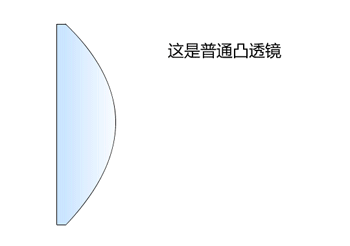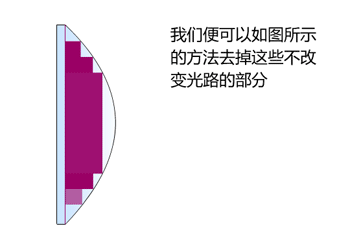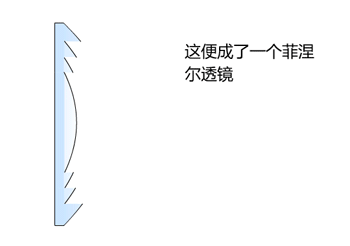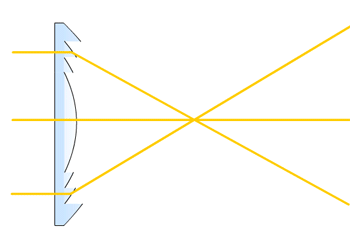
化成一個等效之『薄透鏡』
 。
。
因此在『主平面』之參考系裡,分享著同樣的『成像公式』
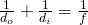
,具有相同『成像條件』, 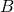 參數為
參數為 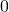
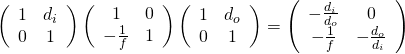 。
。
甚至可以『串接成像』
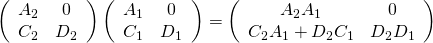
的矣!如是就確定了參數 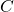 之『聚焦』地位,以及參數
之『聚焦』地位,以及參數 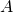 的『影像縮放』性質!!若問為什麼『平面鏡』是理想成像系統的呢?難到原因在於『反射』與『折射』不同耶??但思
的『影像縮放』性質!!若問為什麼『平面鏡』是理想成像系統的呢?難到原因在於『反射』與『折射』不同耶??但思
【曲面折射】
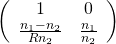 和
和
【曲面反射】
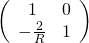
當 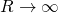 時,參數
時,參數 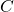 趨近於零﹐等同於『平面』
趨近於零﹐等同於『平面』
【平面折射】
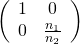 和
和
【平面反射】
 的哩。
的哩。
那為何維基百科特別註記『平面反射』之說明為
Only valid for mirrors perpendicular to the ray.
的呢!!??問題在『小角度』近軸近似下,實在無法表象『任意角度』都能『完美成像』之『理想平面鏡』呀??!!縱使想用著『等同矩陣』
In linear algebra, the identity matrix, or sometimes ambiguously called a unit matrix, of size n is the n × n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context. (In some fields, such as quantum mechanics, the identity matrix is denoted by a boldface one, 1; otherwise it is identical to I.) Less frequently, some mathematics books use U or E to represent the identity matrix, meaning “unit matrix”[1] and the German word “Einheitsmatrix”,[2] respectively.

When A is m×n, it is a property of matrix multiplication that

In particular, the identity matrix serves as the unit of the ring of all n×n matrices, and as the identity element of the general linear group GL(n) consisting of all invertible n×n matrices. (The identity matrix itself is invertible, being its own inverse.)
Where n×n matrices are used to represent linear transformations from an n-dimensional vector space to itself, In represents the identity function, regardless of the basis.
The ith column of an identity matrix is the unit vector ei. It follows that the determinant of the identity matrix is 1 and the trace is n.
Using the notation that is sometimes used to concisely describe diagonal matrices, we can write:

It can also be written using the Kronecker delta notation:

The identity matrix also has the property that, when it is the product of two square matrices, the matrices can be said to be the inverse of one another.
The identity matrix of a given size is the only idempotent matrix of that size having full rank. That is, it is the only matrix such that (a) when multiplied by itself the result is itself, and (b) all of its rows, and all of its columns, are linearly independent.
The principal square root of an identity matrix is itself, and this is its only positive definite square root. However, every identity matrix with at least two rows and columns has an infinitude of symmetric square roots.[3]
………
宣說此理,卻又礙於『物、像』有所不同,亦不可得『計算解析』之好處,不註記,且將如何言之哉???更別講,如果 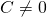 ,同樣『薄透鏡』等效方法也根本不可能使
,同樣『薄透鏡』等效方法也根本不可能使 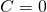 的乎!!!
的乎!!!
pi@raspberrypi:~ $ ipython3
Python 3.4.2 (default, Oct 19 2014, 13:31:11)
Type "copyright", "credits" or "license" for more information.
IPython 2.3.0 -- An enhanced Interactive Python.
? -> Introduction and overview of IPython's features.
%quickref -> Quick reference.
help -> Python's own help system.
object? -> Details about 'object', use 'object??' for extra details.
In [1]: from sympy import *
In [2]: from sympy.physics.optics import FreeSpace, FlatRefraction, ThinLens, GeometricRay, CurvedRefraction, RayTransferMatrix
In [3]: init_printing()
In [4]: A, B, C, D, t1, t2 = symbols('A, B, C, D, t1, t2')
In [5]: 一般ABCD矩陣 = RayTransferMatrix(A, B, C, D)
In [6]: 一般ABCD矩陣
Out[6]:
⎡A B⎤
⎢ ⎥
⎣C D⎦
In [7]: FreeSpace(t2) * 一般ABCD矩陣 * FreeSpace(t1)
Out[7]:
⎡A + C⋅t₂ B + D⋅t₂ + t₁⋅(A + C⋅t₂)⎤
⎢ ⎥
⎣ C C⋅t₁ + D ⎦
In [8]:




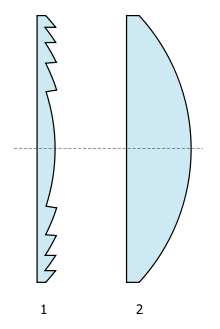
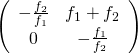
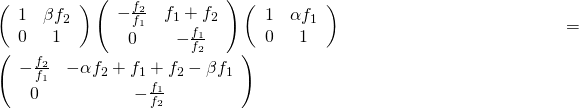
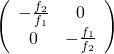








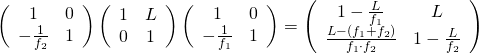
![Rendered by QuickLaTeX.com ipython3 Python 3.4.2 (default, Oct 19 2014, 13:31:11) Type "copyright", "credits" or "license" for more information. IPython 2.3.0 -- An enhanced Interactive Python. ? -> Introduction and overview of IPython's features. %quickref -> Quick reference. help -> Python's own help system. object? -> Details about 'object', use 'object??' for extra details. In [1]: from sympy import * In [2]: from sympy.physics.optics import FreeSpace, FlatRefraction, ThinLens, GeometricRay, CurvedRefraction, RayTransferMatrix In [3]: init_printing() In [4]: f1, L, f2 = symbols('f1, L, f2') In [5]: 相距L之兩薄透鏡組合 = ThinLens(f2) * FreeSpace(L) * ThinLens(f1) In [6]: 相距L之兩薄透鏡組合 Out[6]: ⎡ L ⎤ ⎢ - ── + 1 L ⎥ ⎢ f₁ ⎥ ⎢ ⎥ ⎢ L ⎥ ⎢ - ── + 1 ⎥ ⎢ 1 f₂ L ⎥ ⎢- ── - ──────── - ── + 1⎥ ⎣ f₂ f₁ f₂ ⎦ In [7]: 相距L之兩薄透鏡組合 = 相距L之兩薄透鏡組合.subs(L, f1 + f2) In [8]: 相距L之兩薄透鏡組合 Out[8]: ⎡ f₁ + f₂ ⎤ ⎢ 1 - ─────── f₁ + f₂ ⎥ ⎢ f₁ ⎥ ⎢ ⎥ ⎢ f₁ + f₂ ⎥ ⎢ 1 - ─────── ⎥ ⎢ 1 f₂ f₁ + f₂⎥ ⎢- ── - ─────────── 1 - ───────⎥ ⎣ f₂ f₁ f₂ ⎦ In [9]: 相距L之兩薄透鏡組合 = RayTransferMatrix(相距L之兩薄透鏡組合.A.simplify(), 相距L之兩薄透鏡組合.B.simplify(), 相距L之兩薄透鏡組合.C.simplify(), 相距L之兩 薄透鏡組合.D.simplify()) In [10]: 相距L之兩薄透鏡組合 Out[10]: ⎡-f₂ ⎤ ⎢──── f₁ + f₂⎥ ⎢ f₁ ⎥ ⎢ ⎥ ⎢ -f₁ ⎥ ⎢ 0 ──── ⎥ ⎣ f₂ ⎦ In [11]: </pre> <span style="color: #003300;">,探索其形式實質乎??</span>](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-5f9653dafc9c9b79ec04e693a0ff4dc4_l3.png) \left( \begin{array}{cc}
- \frac{f_2}{f_1} & f_1 + f_2 \\
0 & - \frac{f_1}{f_2} \end{array} \right)
\left( \begin{array}{cc}
- \frac{f_2}{f_1} & f_1 + f_2 \\
0 & - \frac{f_1}{f_2} \end{array} \right) 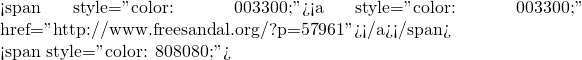 (h, \theta)
(h, \theta) f
f ipython3
Python 3.4.2 (default, Oct 19 2014, 13:31:11)
Type "copyright", "credits" or "license" for more information.
IPython 2.3.0 -- An enhanced Interactive Python.
? -> Introduction and overview of IPython's features.
%quickref -> Quick reference.
help -> Python's own help system.
object? -> Details about 'object', use 'object??' for extra details.
In [1]: from sympy import *
In [2]: from sympy.physics.optics import FreeSpace, FlatRefraction, ThinLens, GeometricRay, CurvedRefraction, RayTransferMatrix
In [3]: init_printing()
In [4]: f1, L, f2 = symbols('f1, L, f2')
In [5]: 相距L之兩薄透鏡組合 = ThinLens(f2) * FreeSpace(L) * ThinLens(f1)
In [6]: 相距L之兩薄透鏡組合
Out[6]:
⎡ L ⎤
⎢ - ── + 1 L ⎥
⎢ f₁ ⎥
⎢ ⎥
⎢ L ⎥
⎢ - ── + 1 ⎥
⎢ 1 f₂ L ⎥
⎢- ── - ──────── - ── + 1⎥
⎣ f₂ f₁ f₂ ⎦
In [7]: 相距L之兩薄透鏡組合 = 相距L之兩薄透鏡組合.subs(L, f1 + f2)
In [8]: 相距L之兩薄透鏡組合
Out[8]:
⎡ f₁ + f₂ ⎤
⎢ 1 - ─────── f₁ + f₂ ⎥
⎢ f₁ ⎥
⎢ ⎥
⎢ f₁ + f₂ ⎥
⎢ 1 - ─────── ⎥
⎢ 1 f₂ f₁ + f₂⎥
⎢- ── - ─────────── 1 - ───────⎥
⎣ f₂ f₁ f₂ ⎦
In [9]: 相距L之兩薄透鏡組合 = RayTransferMatrix(相距L之兩薄透鏡組合.A.simplify(), 相距L之兩薄透鏡組合.B.simplify(), 相距L之兩薄透鏡組合.C.simplify(), 相距L之兩 薄透鏡組合.D.simplify())
In [10]: 相距L之兩薄透鏡組合
Out[10]:
⎡-f₂ ⎤
⎢──── f₁ + f₂⎥
⎢ f₁ ⎥
⎢ ⎥
⎢ -f₁ ⎥
⎢ 0 ──── ⎥
⎣ f₂ ⎦
In [11]: h, θ = symbols('h, θ')
In [12]: 平行光 = GeometricRay(h, θ)
In [13]: 平行光
Out[13]:
⎡h⎤
⎢ ⎥
⎣θ⎦
In [14]: 相距L之兩薄透鏡組合 * 平行光
Out[14]:
⎡ f₂⋅h⎤
⎢θ⋅(f₁ + f₂) - ────⎥
⎢ f₁ ⎥
⎢ ⎥
⎢ -f₁⋅θ ⎥
⎢ ────── ⎥
⎣ f₂ ⎦
In [15]: f, z = symbols('f, z')
In [16]: 行經距離Z = FreeSpace(z)
In [17]: Z處匯聚現象 = 行經距離Z * 相距L之兩薄透鏡組合 * 平行光
In [18]: Z處匯聚現象
Out[18]:
⎡ ⎛ f₁⋅z ⎞ f₂⋅h⎤
⎢θ⋅⎜f₁ - ──── + f₂⎟ - ────⎥
⎢ ⎝ f₂ ⎠ f₁ ⎥
⎢ ⎥
⎢ -f₁⋅θ ⎥
⎢ ────── ⎥
⎣ f₂ ⎦
In [19]:
ipython3
Python 3.4.2 (default, Oct 19 2014, 13:31:11)
Type "copyright", "credits" or "license" for more information.
IPython 2.3.0 -- An enhanced Interactive Python.
? -> Introduction and overview of IPython's features.
%quickref -> Quick reference.
help -> Python's own help system.
object? -> Details about 'object', use 'object??' for extra details.
In [1]: from sympy import *
In [2]: from sympy.physics.optics import FreeSpace, FlatRefraction, ThinLens, GeometricRay, CurvedRefraction, RayTransferMatrix
In [3]: init_printing()
In [4]: f1, L, f2 = symbols('f1, L, f2')
In [5]: 相距L之兩薄透鏡組合 = ThinLens(f2) * FreeSpace(L) * ThinLens(f1)
In [6]: 相距L之兩薄透鏡組合
Out[6]:
⎡ L ⎤
⎢ - ── + 1 L ⎥
⎢ f₁ ⎥
⎢ ⎥
⎢ L ⎥
⎢ - ── + 1 ⎥
⎢ 1 f₂ L ⎥
⎢- ── - ──────── - ── + 1⎥
⎣ f₂ f₁ f₂ ⎦
In [7]: 相距L之兩薄透鏡組合 = 相距L之兩薄透鏡組合.subs(L, f1 + f2)
In [8]: 相距L之兩薄透鏡組合
Out[8]:
⎡ f₁ + f₂ ⎤
⎢ 1 - ─────── f₁ + f₂ ⎥
⎢ f₁ ⎥
⎢ ⎥
⎢ f₁ + f₂ ⎥
⎢ 1 - ─────── ⎥
⎢ 1 f₂ f₁ + f₂⎥
⎢- ── - ─────────── 1 - ───────⎥
⎣ f₂ f₁ f₂ ⎦
In [9]: 相距L之兩薄透鏡組合 = RayTransferMatrix(相距L之兩薄透鏡組合.A.simplify(), 相距L之兩薄透鏡組合.B.simplify(), 相距L之兩薄透鏡組合.C.simplify(), 相距L之兩 薄透鏡組合.D.simplify())
In [10]: 相距L之兩薄透鏡組合
Out[10]:
⎡-f₂ ⎤
⎢──── f₁ + f₂⎥
⎢ f₁ ⎥
⎢ ⎥
⎢ -f₁ ⎥
⎢ 0 ──── ⎥
⎣ f₂ ⎦
In [11]: h, θ = symbols('h, θ')
In [12]: 平行光 = GeometricRay(h, θ)
In [13]: 平行光
Out[13]:
⎡h⎤
⎢ ⎥
⎣θ⎦
In [14]: 相距L之兩薄透鏡組合 * 平行光
Out[14]:
⎡ f₂⋅h⎤
⎢θ⋅(f₁ + f₂) - ────⎥
⎢ f₁ ⎥
⎢ ⎥
⎢ -f₁⋅θ ⎥
⎢ ────── ⎥
⎣ f₂ ⎦
In [15]: f, z = symbols('f, z')
In [16]: 行經距離Z = FreeSpace(z)
In [17]: Z處匯聚現象 = 行經距離Z * 相距L之兩薄透鏡組合 * 平行光
In [18]: Z處匯聚現象
Out[18]:
⎡ ⎛ f₁⋅z ⎞ f₂⋅h⎤
⎢θ⋅⎜f₁ - ──── + f₂⎟ - ────⎥
⎢ ⎝ f₂ ⎠ f₁ ⎥
⎢ ⎥
⎢ -f₁⋅θ ⎥
⎢ ────── ⎥
⎣ f₂ ⎦
In [19]:
![Rendered by QuickLaTeX.com ipython3 Python 3.4.2 (default, Oct 19 2014, 13:31:11) Type "copyright", "credits" or "license" for more information. IPython 2.3.0 -- An enhanced Interactive Python. ? -> Introduction and overview of IPython's features. %quickref -> Quick reference. help -> Python's own help system. object? -> Details about 'object', use 'object??' for extra details. In [1]: from sympy import * In [2]: from sympy.physics.optics import FreeSpace, FlatRefraction, ThinLens, GeometricRay, CurvedRefraction, RayTransferMatrix In [3]: init_printing() In [4]: f1, L, f2 = symbols('f1, L, f2') In [5]: 相距L之兩薄透鏡組合 = ThinLens(f2) * FreeSpace(L) * ThinLens(f1) In [6]: 相距L之兩薄透鏡組合 Out[6]: ⎡ L ⎤ ⎢ - ── + 1 L ⎥ ⎢ f₁ ⎥ ⎢ ⎥ ⎢ L ⎥ ⎢ - ── + 1 ⎥ ⎢ 1 f₂ L ⎥ ⎢- ── - ──────── - ── + 1⎥ ⎣ f₂ f₁ f₂ ⎦ In [7]: 相距L之兩薄透鏡組合.C.expand() Out[7]: L 1 1 ───── - ── - ── f₁⋅f₂ f₂ f₁ In [8]: 前主平面 = (1 - 相距L之兩薄透鏡組合.D) / 相距L之兩薄透鏡組合.C In [9]: 前主平面.expand() Out[9]: L ─────────── L f₂ ── - 1 - ── f₁ f₁ In [10]: 後主平面 = (1 - 相距L之兩薄透鏡組合.A) / 相距L之兩薄透鏡組合.C In [11]: 後主平面.expand() Out[11]: L ─────────── L f₁ ── - ── - 1 f₂ f₂ In [12]: 等效薄透鏡 = FreeSpace(後主平面.expand()) * 相距L之兩薄透鏡組合 * FreeSpace(前主平面.expand()) In [13]: 等效薄透鏡.A.simplify() Out[13]: 1 In [14]: 等效薄透鏡.B.simplify() Out[14]: 0 In [15]: 等效薄透鏡.C.simplify() Out[15]: L - f₁ - f₂ ─────────── f₁⋅f₂ In [16]: 等效薄透鏡.D.simplify() Out[16]: 1 In [17]: </pre> <span style="color: #003300;">豈非是大自然『得色』者耶!!??然而雖想更上一層樓,也欲窮『千里目』 ,無奈遠方『視角』太小</span> <h1 id="firstHeading" class="firstHeading" lang="en"><span style="color: #003300;"><a style="color: #003300;" href="https://en.wikipedia.org/wiki/Angle_of_view">Angle of view</a></span></h1> <span style="color: #808080;">In <a style="color: #808080;" title="Photography" href="https://en.wikipedia.org/wiki/Photography">photography</a>, <b>angle of view</b> (<b>AOV</b>)<sup id="cite_ref-1" class="reference"><a style="color: #808080;" href="https://en.wikipedia.org/wiki/Angle_of_view#cite_note-1">[1]</a></sup> describes the <a style="color: #808080;" title="Angle" href="https://en.wikipedia.org/wiki/Angle">angular</a> extent of a given scene that is imaged by a <a style="color: #808080;" title="Camera" href="https://en.wikipedia.org/wiki/Camera">camera</a>. It is used interchangeably with the more general term <a style="color: #808080;" title="Field of view" href="https://en.wikipedia.org/wiki/Field_of_view">field of view</a>.</span> <img class="alignnone size-full wp-image-58491" src="http://www.freesandal.org/wp-content/uploads/425px-Angle_of_view.svg.png" alt="425px-Angle_of_view.svg" width="425" height="351" /> <span style="color: #999999;">A camera's <b>angle of view</b> can be measured horizontally, vertically, or diagonally.</span> <span style="color: #808080;">It is important to distinguish the angle of view from the <b>angle of coverage</b>, which describes the angle range that a lens can image. Typically the <a style="color: #808080;" title="Image circle" href="https://en.wikipedia.org/wiki/Image_circle">image circle</a> produced by a lens is large enough to cover the film or sensor completely, possibly including some <a style="color: #808080;" title="Vignetting" href="https://en.wikipedia.org/wiki/Vignetting">vignetting</a> toward the edge. If the angle of coverage of the lens does not fill the sensor, the image circle will be visible, typically with strong vignetting toward the edge, and the effective angle of view will be limited to the angle of coverage.</span> <span style="color: #808080;">A camera's angle of view depends not only on the lens, but also on the sensor. Digital sensors are usually smaller than <a class="mw-redirect" style="color: #808080;" title="35mm film" href="https://en.wikipedia.org/wiki/35mm_film">35mm film</a>, and this causes the lens to have a narrower angle of view than with 35mm film, by a constant factor for each sensor (called the <a style="color: #808080;" title="Crop factor" href="https://en.wikipedia.org/wiki/Crop_factor">crop factor</a>). In everyday digital cameras, the crop factor can range from around 1 (professional <a class="mw-redirect" style="color: #808080;" title="Digital SLR" href="https://en.wikipedia.org/wiki/Digital_SLR">digital SLRs</a>), to 1.6 (consumer SLR), to 2 (<a class="mw-redirect" style="color: #808080;" title="Micro Four Thirds" href="https://en.wikipedia.org/wiki/Micro_Four_Thirds">Micro Four Thirds</a> ILC) to 4 (<a class="new" style="color: #808080;" title="Enthusiast compact camera (page does not exist)" href="https://en.wikipedia.org/w/index.php?title=Enthusiast_compact_camera&action=edit&redlink=1">enthusiast compact cameras</a>) to 6 (most <a class="mw-redirect" style="color: #808080;" title="Compact camera" href="https://en.wikipedia.org/wiki/Compact_camera">compact cameras</a>). So a standard 50mm lens for 35mm photography acts like a 50mm standard "film" lens even on a professional digital SLR, but would act closer to an 80mm lens (1.6 x 50mm) on many mid-market DSLRs, and the 40 degree angle of view of a standard 50mm lens on a film camera is equivalent to a 28 - 35mm lens on many digital SLRs.</span> <img class="alignnone size-full wp-image-58490" src="http://www.freesandal.org/wp-content/uploads/Angle_of_View_F_V_Chambers_1916.png" alt="Angle_of_View_F_V_Chambers_1916" width="759" height="714" /> <span style="color: #999999;">In 1916, Northey showed how to calculate the angle of view using ordinary carpenter's tools.<sup id="cite_ref-2" class="reference"><a style="color: #999999;" href="https://en.wikipedia.org/wiki/Angle_of_view#cite_note-2">[2]</a></sup> The angle that he labels as the angle of view is the half-angle or "the angle that a straight line would take from the extreme outside of the field of view to the center of the lens;" he notes that manufacturers of lenses use twice this angle.</span> <img class="alignnone size-full wp-image-58489" src="http://www.freesandal.org/wp-content/uploads/Camera_focal_length_distance_house_animation.gif" alt="Camera_focal_length_distance_house_animation" width="512" height="512" /> <span style="color: #999999;">In this simulation, adjusting the angle of view and distance of the camera while keeping the object in frame results in vastly differing images. At distances approaching infinity, the light rays are nearly parallel to each other, resulting in a "flattened" image. At low distances and high angles of view objects appear "foreshortened".</span> <h3><span id="Derivation_of_the_angle-of-view_formula" class="mw-headline" style="color: #808080;">Derivation of the angle-of-view formula</span></h3> <span style="color: #808080;">Consider a rectilinear lens in a camera used to photograph an object at a distance <img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/5bf84e7fd4fb8259a9b37f956afdf83ee2a020f9" alt="S_{1}" />, and forming an image that just barely fits in the dimension, <img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e85ff03cbe0c7341af6b982e47e9f90d235c66ab" alt="d" />, of the frame (the <a style="color: #808080;" title="Photographic film" href="https://en.wikipedia.org/wiki/Photographic_film">film</a> or <a style="color: #808080;" title="Image sensor" href="https://en.wikipedia.org/wiki/Image_sensor">image sensor</a>). Treat the lens as if it were a <a style="color: #808080;" title="Pinhole camera model" href="https://en.wikipedia.org/wiki/Pinhole_camera_model">pinhole</a> at distance <img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1143e284d5f25cef778ab482edf6617a523ddd9f" alt="S_{2}" /> from the image plane (technically, the <a class="new" style="color: #808080;" title="Center of perspective (page does not exist)" href="https://en.wikipedia.org/w/index.php?title=Center_of_perspective&action=edit&redlink=1">center of perspective</a> of a <a style="color: #808080;" title="Rectilinear lens" href="https://en.wikipedia.org/wiki/Rectilinear_lens">rectilinear lens</a> is at the center of its <a style="color: #808080;" title="Entrance pupil" href="https://en.wikipedia.org/wiki/Entrance_pupil">entrance pupil</a>):<sup id="cite_ref-7" class="reference"><a style="color: #808080;" href="https://en.wikipedia.org/wiki/Angle_of_view#cite_note-7">[7]</a></sup></span> <img class="alignnone size-full wp-image-58488" src="http://www.freesandal.org/wp-content/uploads/Lens_angle_of_view.svg.png" alt="Lens_angle_of_view.svg" width="535" height="340" /> <span style="color: #808080;">Now <img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/dc94aaeb93d142252c471643dea5826c78797fdd" alt="\alpha /2" /> is the angle between the <a style="color: #808080;" title="Optical axis" href="https://en.wikipedia.org/wiki/Optical_axis">optical axis</a> of the lens and the ray joining its optical center to the edge of the film. Here <img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/b79333175c8b3f0840bfb4ec41b8072c83ea88d3" alt="\alpha " /> is defined to be the angle-of-view, since it is the angle enclosing the largest object whose image can fit on the film. We want to find the relationship between:</span> <dl><dd><dl><dd><span style="color: #808080;">the angle <img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/b79333175c8b3f0840bfb4ec41b8072c83ea88d3" alt="\alpha " /></span></dd><dd><span style="color: #808080;">the "opposite" side of the right triangle, <img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/582b6455b1ff5f4fb027024a8b1458687dc8ed74" alt="d/2" /> (half the film-format dimension)</span></dd><dd><span style="color: #808080;">the "adjacent" side, <img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1143e284d5f25cef778ab482edf6617a523ddd9f" alt="S_{2}" /> (distance from the lens to the image plane)</span></dd></dl></dd></dl><span style="color: #808080;">Using basic trigonometry, we find:</span> <dl><dd><dl><dd><span style="color: #808080;"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y"> </span><img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/61a28fda5183c97596d8ab9849e2e1f465dc9fc6" alt="\tan(\alpha /2)={\frac {d/2}{S_{2}}}." /></span></dd></dl></dd></dl><span style="color: #808080;">which we can solve for <i>α</i>, giving:</span> <dl><dd><dl><dd><span style="color: #808080;"><img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1ba196939e86f14fd3436381db8408d87c1e5221" alt="\alpha =2\arctan {\frac {d}{2S_{2}}}" /></span></dd></dl></dd></dl><span style="color: #808080;">To project a sharp image of distant objects, <span class="mwe-math-mathml-inline mwe-math-mathml-a11y"> S 2 {\displaystyle S_{2}} </span><img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1143e284d5f25cef778ab482edf6617a523ddd9f" alt="S_{2}" /> needs to be equal to the <a style="color: #808080;" title="Focal length" href="https://en.wikipedia.org/wiki/Focal_length">focal length</a>, <span class="mwe-math-mathml-inline mwe-math-mathml-a11y"> F {\displaystyle F} </span><img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/545fd099af8541605f7ee55f08225526be88ce57" alt="F" />, which is attained by setting the lens for <a style="color: #808080;" title="Infinity focus" href="https://en.wikipedia.org/wiki/Infinity_focus">infinity focus</a>. Then the angle of view is given by:</span> <dl><dd><dl><dd><span style="color: #808080;"><img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e141c70c4127fcf2d2d59ac41c7f3c5f82307f33" alt="\alpha =2\arctan {\frac {d}{2f}}" /> where <img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/7383360bd488f252a2dc801771d612354e922d43" alt="f=F" /></span></dd></dl></dd></dl><span style="color: #808080;">Note that the angle of view varies slightly when the focus is not at infinity (See <a style="color: #808080;" title="Breathing (lens)" href="https://en.wikipedia.org/wiki/Breathing_%28lens%29">breathing (lens)</a>), given by <img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/0a31381c48040e54461d782092f627f2a2f69b02" alt="S_{2}={\frac {S_{1}f}{S_{1}-f}}" /> rearranging the lens equation.</span> <h4><span id="Macro_photography" class="mw-headline" style="color: #808080;">Macro photography</span></h4> <span style="color: #808080;">For macro photography, we cannot neglect the difference between <img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1143e284d5f25cef778ab482edf6617a523ddd9f" alt="S_{2}" /> and <img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/545fd099af8541605f7ee55f08225526be88ce57" alt="F" />. From the <a style="color: #808080;" title="Lens (optics)" href="https://en.wikipedia.org/wiki/Lens_%28optics%29#Imaging_properties">thin lens formula</a>,</span> <dl><dd><dl><dd><span style="color: #808080;"><img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1c06e062467b759014f591ce6c1b25448a4fe12f" alt="{\frac {1}{F}}={\frac {1}{S_{1}}}+{\frac {1}{S_{2}}}" />.</span></dd></dl></dd></dl><span style="color: #808080;">From the definition of <a style="color: #808080;" title="Magnification" href="https://en.wikipedia.org/wiki/Magnification">magnification</a>, <img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9dd92ab3eac5d8b98d6a8bbae9d96c5f6bba41ae" alt="m=S_{2}/S_{1}" />, we can substitute <img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/5bf84e7fd4fb8259a9b37f956afdf83ee2a020f9" alt="S_{1}" /> and with some algebra find:</span> <dl><dd><dl><dd><span style="color: #808080;"><img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f497867326b3486b5dee64b743486682f6c89bf3" alt="S_{2}=F\cdot (1+m)" /></span></dd></dl></dd></dl><span style="color: #808080;">Defining <img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/7fa764b3e6e147a38405ed027f28465136fa7b3a" alt="f=S_{2}" /> as the "effective focal length", we get the formula presented above:</span> <dl><dd><dl><dd><span style="color: #808080;"><img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e141c70c4127fcf2d2d59ac41c7f3c5f82307f33" alt="\alpha =2\arctan {\frac {d}{2f}}" /> where <img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/a7b5bad6d59188c6f93c1b7dfa359d82cdf36c23" alt="f=F\cdot (1+m)" />.</span></dd></dl></dd></dl><span style="color: #808080;">A second effect which comes into play in macro photography is lens asymmetry (an asymmetric lens is a lens where the aperture appears to have different dimensions when viewed from the front and from the back). The lens asymmetry causes an offset between the nodal plane and pupil positions. The effect can be quantified using the ratio (<i>P</i>) between apparent exit pupil diameter and entrance pupil diameter. The full formula for angle of view now becomes:<sup id="cite_ref-Paul_van_Walree_2009_5-1" class="reference"><a style="color: #808080;" href="https://en.wikipedia.org/wiki/Angle_of_view#cite_note-Paul_van_Walree_2009-5">[5]</a></sup></span> <dl><dd><dl><dd><span style="color: #808080;"><img class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/4f8a08d31928d73dfb0bc437bbd904a286ba2a05" alt="\alpha =2\arctan {\frac {d}{2F\cdot (1+m/P)}}" /></span></dd></dl></dd></dl><span style="color: #003300;">東西又太遙,焉能得</span> <h1 id="firstHeading" class="firstHeading" lang="zh-TW"><span style="color: #003300;"><a style="color: #003300;" href="https://zh.wikipedia.org/zh-tw/%E5%AA%BD%E7%A5%96">媽祖</a></span></h1> <span style="color: #808080;"><b>媽祖</b>(<a style="color: #808080;" title="莆仙語" href="https://zh.wikipedia.org/wiki/%E8%8E%86%E4%BB%99%E8%AA%9E">莆仙語</a>:<span lang="cpx" xml:lang="cpx"><b>Mâ-cô</b></span>;<a class="mw-redirect" style="color: #808080;" title="閩南語" href="https://zh.wikipedia.org/wiki/%E9%96%A9%E5%8D%97%E8%AA%9E">閩南語</a>:<span lang="nan" xml:lang="nan"><b>Má-chó͘</b></span>;<a style="color: #808080;" title="閩東語" href="https://zh.wikipedia.org/wiki/%E9%96%A9%E6%9D%B1%E8%AA%9E">閩東語</a>:<span lang="cdo" xml:lang="cdo"><b>Mā-cū</b></span>)是以<a style="color: #808080;" title="中國" href="https://zh.wikipedia.org/wiki/%E4%B8%AD%E5%9C%8B">中國</a>東南沿海為中心、包括<a class="mw-redirect" style="color: #808080;" title="東亞" href="https://zh.wikipedia.org/wiki/%E6%9D%B1%E4%BA%9E">東亞</a>(<a style="color: #808080;" title="琉球" href="https://zh.wikipedia.org/wiki/%E7%90%89%E7%90%83">琉球</a>、<a style="color: #808080;" title="日本" href="https://zh.wikipedia.org/wiki/%E6%97%A5%E6%9C%AC">日本</a>及<a class="mw-redirect" style="color: #808080;" title="東南亞" href="https://zh.wikipedia.org/wiki/%E6%9D%B1%E5%8D%97%E4%BA%9E">東南亞</a>)沿海地區<sup id="cite_ref-.E6.BF.B1.E4.B8.8B.E6.AD.A6.E5.BF.972009_1-0" class="reference"><a style="color: #808080;" href="https://zh.wikipedia.org/wiki/%E5%AA%BD%E7%A5%96#cite_note-.E6.BF.B1.E4.B8.8B.E6.AD.A6.E5.BF.972009-1">[1]</a></sup>的<a class="mw-redirect mw-disambig" style="color: #808080;" title="海神" href="https://zh.wikipedia.org/wiki/%E6%B5%B7%E7%A5%9E">海神</a>信仰,又稱<b>天上聖母</b> 、<b>天后聖母</b>、<b>天后</b>、<b>天后娘娘</b>、<b>天妃</b>、<b>天妃娘娘</b>、<b>湄洲娘媽</b>等<sup id="cite_ref-.E8.81.96.E6.AD.8C_2-0" class="reference"><a style="color: #808080;" href="https://zh.wikipedia.org/wiki/%E5%AA%BD%E7%A5%96#cite_note-.E8.81.96.E6.AD.8C-2">[2]</a></sup>。媽祖的影響力由福建<a class="mw-redirect" style="color: #808080;" title="湄洲" href="https://zh.wikipedia.org/wiki/%E6%B9%84%E6%B4%B2">湄洲</a>傳播開來 ,歷經千百年,對於<a class="mw-redirect" style="color: #808080;" title="東亞" href="https://zh.wikipedia.org/wiki/%E6%9D%B1%E4%BA%9E">東亞</a>海洋文化及<a style="color: #808080;" title="中國" href="https://zh.wikipedia.org/wiki/%E4%B8%AD%E5%9C%8B">中國</a>沿海文化產生重大的影響 ,被學者們稱為<b>媽祖文化</b>。2009年10月,媽祖信仰入選<a class="mw-redirect" style="color: #808080;" title="聯合國教科文組織" href="https://zh.wikipedia.org/wiki/%E8%81%AF%E5%90%88%E5%9C%8B%E6%95%99%E7%A7%91%E6%96%87%E7%B5%84%E7%B9%94">聯合國教科文組織</a><a style="color: #808080;" title="人類非物質文化遺產代表作名錄" href="https://zh.wikipedia.org/wiki/%E4%BA%BA%E7%B1%BB%E9%9D%9E%E7%89%A9%E8%B4%A8%E6%96%87%E5%8C%96%E9%81%97%E4%BA%A7%E4%BB%A3%E8%A1%A8%E4%BD%9C%E5%90%8D%E5%BD%95">人類非物質文化遺產代表作名錄</a>。</span> <img class="alignnone size-full wp-image-58492" src="http://www.freesandal.org/wp-content/uploads/1280px-Main_statue_of_Datianhou_Temple.jpg" alt="1280px-Main_statue_of_Datianhou_Temple" width="1280" height="960" /> <h2><span id=".E7.9B.B8.E9.97.9C.E5.82.B3.E8.AA.AA" class="mw-headline" style="color: #808080;">相關傳說</span></h2> <h3><span id=".E5.8D.83.E9.87.8C.E7.9C.BC.E9.A0.86.E9.A2.A8.E8.80.B3" class="mw-headline" style="color: #808080;">千里眼順風耳</span></h3> <span style="color: #808080;">在一般的傳說裡,替媽祖察、聽世情的兩大駕前護衛神分別為左手持<a style="color: #808080;" title="方天畫戟" href="https://zh.wikipedia.org/wiki/%E6%96%B9%E5%A4%A9%E7%95%AB%E6%88%9F">方天畫戟</a>,右手舉至額前做遠視狀的<a style="color: #808080;" title="千里眼" href="https://zh.wikipedia.org/wiki/%E5%8D%83%E9%87%8C%E7%9C%BC">千里眼</a>(又稱<a class="new" style="color: #808080;" title="金精將軍(頁面不存在)" href="https://zh.wikipedia.org/w/index.php?title=%E9%87%91%E7%B2%BE%E5%B0%87%E8%BB%8D&action=edit&redlink=1">金精將軍</a>),以及左手持<a class="new" style="color: #808080;" title="月眉斧頭(頁面不存在)" href="https://zh.wikipedia.org/w/index.php?title=%E6%9C%88%E7%9C%89%E6%96%A7%E9%A0%AD&action=edit&redlink=1">月眉斧頭</a>,右手舉至側耳作聽音狀的<a style="color: #808080;" title="順風耳" href="https://zh.wikipedia.org/wiki/%E9%A0%86%E9%A2%A8%E8%80%B3">順風耳</a>(又稱<a class="new" style="color: #808080;" title="水精將軍(頁面不存在)" href="https://zh.wikipedia.org/w/index.php?title=%E6%B0%B4%E7%B2%BE%E5%B0%87%E8%BB%8D&action=edit&redlink=1">水精將軍</a>)。</span> <span style="color: #003300;">的千里眼與順風耳,效法其視聽分明救苦救難之精神乎??!!</span> 其實這『縮地』之術、『近天』之法,古來早已知之 <span style="color: #ff9900;">當](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-89aac1c7ae6968e3b222c46fb2347958_l3.png) L = f_1 + f_2
L = f_1 + f_2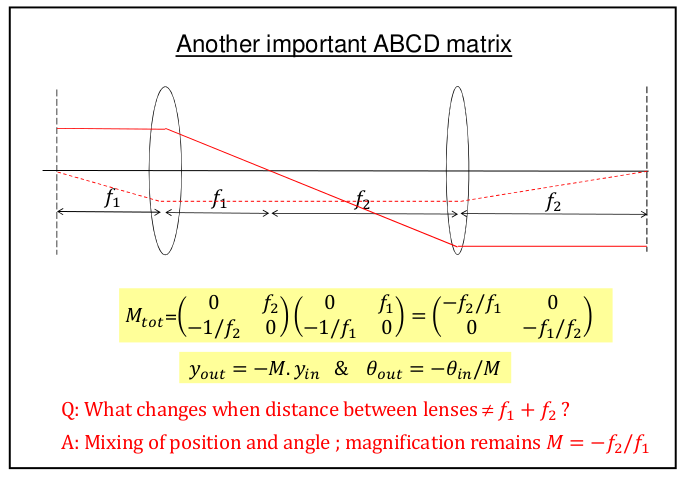




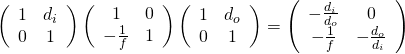 。
。


