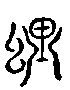時間序列︰生成函數‧漸近展開︰白努利 □○《十右》

2017-04-05 懸鉤子

一張圖暗示白努利多項式 $B_n(x) = \sum \limits_{k=0}^{n} \binom {n}k B_k x^{n-k}$

，在 $x=\frac{1}{2}$ 處似乎具有奇偶函數『對稱性』

Symmetry

Symmetry (from Greek συμμετρία symmetria “agreement in dimensions, due proportion, arrangement”)^[1] in everyday language refers to a sense of harmonious and beautiful proportion and balance.^[2]^[3]^[a] In mathematics, “symmetry” has a more precise definition, that an object is invariant to any of various transformations; including reflection, rotation or scaling. Although these two meanings of “symmetry” can sometimes be told apart, they are related, so they are here discussed together.

Mathematical symmetry may be observed with respect to the passage of time; as a spatial relationship; through geometric transformations; through other kinds of functional transformations; and as an aspect of abstract objects, theoretic models, language, music and even knowledge itself.^[4]^[b]

This article describes symmetry from three perspectives: in mathematics, including geometry, the most familiar type of symmetry for many people; in science and nature; and in the arts, covering architecture, art and music.

The opposite of symmetry is asymmetry.

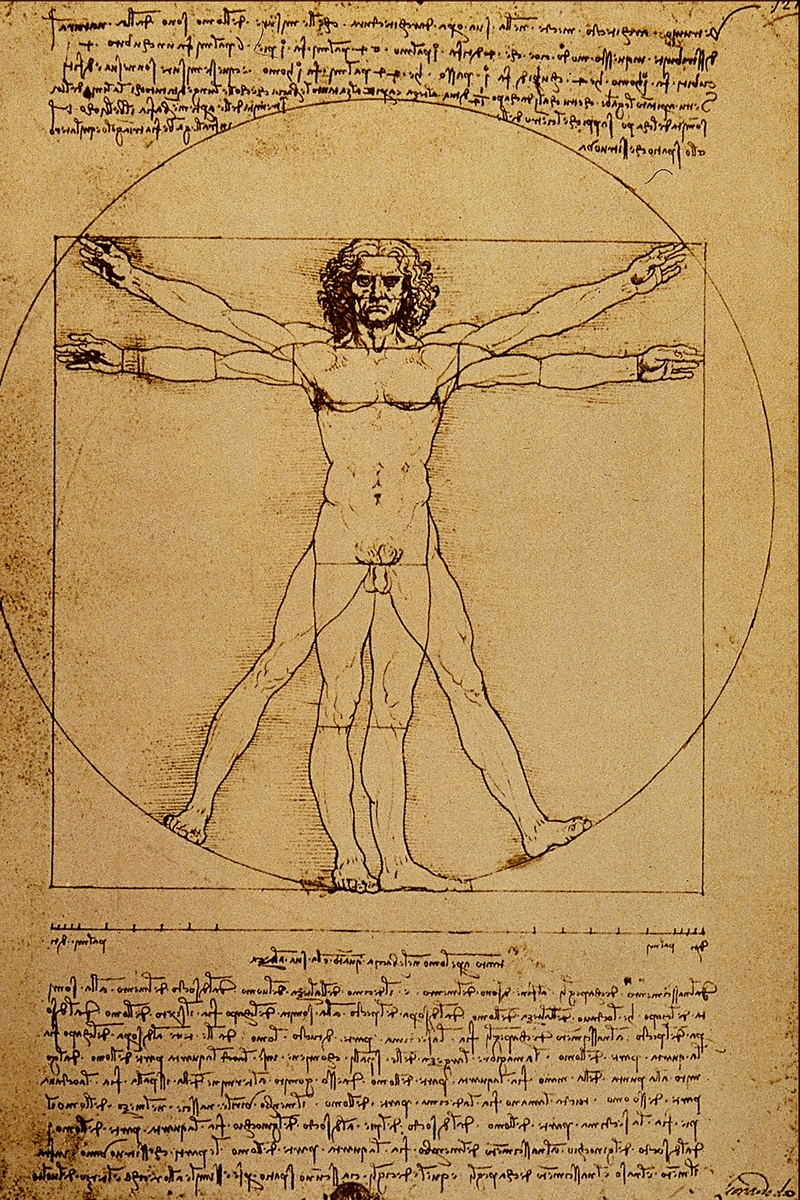
Leonardo da Vinci‘s ‘Vitruvian Man‘ (ca. 1487) is often used as a representation of symmetry in the human body and, by extension, the natural universe.

的呦！將要如何探討呢？如果白努利多項式 $B_n (x)$ 在『對稱座標系』 $x^{'}$ 裡滿足 $B_n(- x^{'}) = \mp B_n ({x}^{'}) , \ x^{'} \ge 0$ ﹐那麼在原作標系 $x$ 裡， $-x{'}$ 的座標為 $x_{-} = \frac{1}{2}- x^{'}$ ； $x^{'}$ 的座標是 $x_{+} = \frac{1}{2} + x^{'}$ 。如是所謂『對稱點』之間的關係 $(- x^{'}) + x^{'} = 0$ ，就可以表述成 $x_{-} + x_{+} = 2 \cdot \frac{1}{2} = 1$ ，而且 $\ B_n (\frac{1}{2}- x^{'}) = \mp B_n(\frac{1}{2} + x^{'})$ 。這正建議我們求得 $B_n (1-x)$ 與 $B_n(x)$ 之關係耶？？因為 $x^{'}$ 和 $x$ 座標系間的『座標變換』不就是 $x = \frac{1}{2} + x^{'}$ 乎！！切莫混淆『性質關係』和『座標計算』也☆

因此我們可藉著白努利多項式之生成函數 $\sum \limits_{n=0}^{\infty} B_n (x) \frac{t^n}{n!} = \frac{t}{e^t - 1} \cdot e^{xt}$ 推導如下︰

$\sum \limits_{n=0}^{\infty} B_n (1-x) \frac{t^n}{n!} = \frac{t}{e^t - 1} \cdot e^{(1-x)t}$

$= \frac{-(-t)}{e^{-(-t)} - 1} \cdot e^{(1-x)(-(-t))} \cdot \frac{e^{(-t)}}{e^{(-t)}}$

$= \frac{(-t) e^{x(-t)}}{e^{(-t)} - 1}$

$= \sum \limits_{n=0}^{\infty} B_n (x) \frac{{(-t)}^n}{n!}$

$\therefore B_n (1-x) = {(-1)}^n B_n (x), \ n \ge 0$ 。

果真是奇次偶次方符合奇偶函數矣！！

俗諺說︰嚴以律己，寬以待人。就是待人處事之道吧！！？？追求言論自由，理不應尊重人言、自重己言嗎？？！！此乃『對稱性』在宇宙人生中之重要性也☆

總是有故事可讀的哩★

蕩寇志

《蕩寇志》是中國清代小說家俞萬春對明代小說《水滸傳》的續寫，又稱《結水滸全傳》或《結水滸傳》。全書緊接著《水滸傳》第七十回「忠義堂石碣受天文梁山泊英雄驚惡夢」的故事，從第七十一回到第一百四十回，共七十回，末附「結子」一回。

……

序

這一部書，名喚作《蕩寇志》。看官，你道這書為何而作？緣施耐庵先生《水滸傳》並不以宋江為忠義。眾位只須看他一路筆意，無一字不描寫宋江的奸惡。其所以稱他忠義者，正為口裡忠義，心裡強盜，愈形出大奸大惡也。聖歎先生批得明明白白：忠於何在？義於何在？總而言之，既是忠義必不做強盜，既是強盜必不算忠義。乃有羅貫中者，忽撰出一部《後水滸》來，竟說得宋江是真忠真義。從此天下後世做強盜的，無不看了宋江的樣：心裡強盜，口裡忠義。殺人放火也叫忠義，打家劫舍也叫忠義，戕官拒捕、攻城陷邑也叫忠義。看官你想，這喚做什麼說話？真是邪說淫辭，壞人心術，貽害無窮。此等書，若容他存留人間，成何事體！莫道小說閒書不關緊要，須知越是小說閒書越發播傳得快，茶坊酒肆，燈前月下，人人喜說，個個愛聽。他這部書既已刊刻行世，在下亦不能禁止他。因想當年宋江，並沒有受招安、平方臘的話，只有被張叔夜擒拿正法一句話。如今他既妄造偽言，抹煞真事。我亦何妨提明真事，破他偽言，使天下後世深明盜賊、忠義之辨，絲毫不容假借。況夢中既受囑於真靈，燈下更難已於筆墨。看官須知：這部書乃是結耐庵之《前水滸傳》，與《後水滸》絕無交涉也。本意已明，請看正傳。

山陰忽來道人俞萬春仲華甫手著

………

第一百三十一回雲天彪旗分五色　呼延灼力殺四門

次日，呼延灼、魏定國領兵潛地移向西門，果然神不知鬼不覺，直抵城下。呼延灼暗傳號令，眾賊一齊布上雲梯。只聽得城裡一聲號炮，官兵一齊立出，城上槍炮卷馳，矢石齊下，賊人紛紛驚退。呼延灼大怒，驟馬出陣，大叫道：「賊匹夫，來與我廝殺一場！」哈蘭生開了城門，提著銅人打出。呼延灼即忙迎住。兩馬相交，軍器並舉，兩個各使出本身神力，狠命相爭。只見銅人一振，真是重鼎千鈞；鞭影雙揮，但覺寒光兩道。兩個一來一往，一去一還，也鬥到四十餘合。忽聽得陣後人聲沸亂，呼延灼只顧前面，不敢還顧，魏定國即忙轉身押陣，聞達已衝入陣中。魏定國即忙指揮陣騎，豁地分為兩隊，兩隊各用強弓勁弩射來。聞達那邊衝突一回，不能取勝。聞達暗想道：「此人本是一勇之夫，不難取他，只是攻擊得緊，他必死命相拒。看來此事，事寬則圓，急難成效。」便急領鐵騎退出陣中。魏定國果然驟馬追出，聞達轉身迎住。鬥到二十餘合，聞達賣個破綻，勒馬便走，仍使出那個擒單廷?的手法來。說也不信，那魏定國果然照樣上鉤。聞達揮轉刀鋒，砍傷左腿，魏定國翻身下馬，官軍一齊上，捆捉去了。呼延灼正與哈蘭生廝殺，忽聞報魏定國又被擒，大驚，急架住了哈蘭生，縱出圈子，無心戀戰，急領軍馬走了。聞達帶領鐵騎，押著魏定國，隨了哈蘭生，一同進城。天彪見連日擒獲兩將，大喜，對諸將道：「來日呼延灼若再不走，可用全軍逐之。我看他兵卒離心，必不能相持也。」眾將領諾。
到了次日，呼延灼果惡狠狠領兵來攻南門。天彪吩咐開門，倒提青龍偃月刀，一馬先出。呼延灼正待迎敵，只聽得城上接連九個號炮，擂鼓振天，官軍吶喊齊出，勢如潮湧，疾如風生，駭如雷崩，奮如電掣，賊兵不及迎戰，早已潰亂。呼延灼大驚，無心戀戰，撥馬飛逃。官軍遮天蓋地價殺來，賊兵紛紛四散，霎時間長風掃籜，開除淨盡。呼延灼匹馬落荒而走。

───

樹莓派、樹莓派之學習、樹莓派之教育

時間序列︰生成函數‧漸近展開︰白努利 □○《十中》

2017-04-04 懸鉤子

求知者有所求乎？

天地一沙鷗，
海天成一色，
人立天地間！

《莊子‧秋水》上說了一則故事︰

莊子釣於濮水，楚王使大夫二人往先焉，曰：『願以境內累矣！』 莊子持竿不顧，曰：『吾聞楚有神龜，死已三千歲矣，王巾笥而藏之廟堂之上。此龜者，寧其死為留骨而貴乎，寧其生而曳尾於塗中乎？』二大夫曰：『寧生而曳尾塗中。』莊子曰：『往矣！吾將曳尾於塗中。』

，然後在《莊子‧養生主》中又講︰

吾生也有涯，而知也無涯。以有涯隨無涯，殆已；已而為知者，殆而已矣。為善無近名，為惡無近刑，緣督以為經，可以保身，可以全生，可以養親，可以盡年。

難道莊子是反對『學習』的嗎？也許相互對比著看，或許他祇想說生物的貪生怕死自然而然，然而人卻自以為貴又喜歡追名逐利，這根本不是為著知，僅是想知道更多『有用的』東西，他擔心如果人連『生命』都保不住了，那『學問』又有什麼用呢？？

學問果真無境界耶？？

任教於水木清華又是四大導師之一的王國維先生在他的大作《人間詞話》裡說到他『治學經驗』，是這麼講的

古今之成大事業、大學問者，必須經過三種之境界︰『昨夜西風凋碧樹，獨上高樓，望盡天涯路。』此第一境也。『衣帶漸寬終不悔，為伊消得人憔悴。』此第二境也。『眾裡尋他千百度，回頭暮見，那人正在，燈火欄珊處。』此第三境也。

作者並不能知道他為何『錯記』或是『記錯』了第三個境界？那裡寫的『眾裡尋他千百度，回頭暮見，那人正在，燈火欄珊處。』當是辛棄疾的《青玉案 ‧元夕》之『眾裡尋他千百度。驀然回首，那人卻在，燈火闌珊處。』。或許就像德國的大心理學家西格蒙德·佛洛伊德的『夢的解析』一書所說的︰要講『遺忘』一事到底是何事呢？此事總發生於過去卻又老是影響著當下和未來！！

就讓我們自己踏入那河中哪怕只是一次；

蝶戀花 北宋晏殊

檻菊愁煙蘭泣露，
羅幕輕寒，
燕子雙飛去。
明月不諳離恨苦，
斜光到曉穿朱戶。
昨夜西風凋碧樹，
獨上高樓，
望盡天涯路。
欲寄彩箋兼尺素，
山長水闊知何處？

蝶戀花 北宋柳永

佇倚危樓風細細，望極春愁，黯黯生天際。
草色煙光殘照裏，無言誰會憑闌意？
擬把疏狂圖一醉，對酒當歌，強樂還無味。
衣帶漸寬終不悔，為伊消得人憔悴。

青玉案‧元夕 南宋辛棄疾

東風夜放花千樹，更吹落、星如雨。
寶馬雕車香滿路。鳳簫聲動，玉壺光轉，一夜魚龍舞。
蛾兒雪柳黃金縷，笑語盈盈暗香去。眾裡尋他千百度。
驀然回首，那人卻在，燈火闌珊處。

；去感受那大地迴旋之流水淙淙，…往通向…心靈的一扇門扉…

─── 摘自《後生可畏!？》

既已知

白努利數起源於等冪求和公式

Faulhaber’s formula

Theorem

Let n and p be positive integers.

Then:

$\sum \limits_{k = 1}^n k^p = \frac 1 {p + 1} \sum \limits_{i = 0}^p \left({-1}\right)^i \binom {p + 1} i B_i n^{p + 1 - i}$

where Bn denotes the nth Bernoulli number.

─── 摘自《時間序列︰生成函數‧漸近展開︰白努利 □○《四》》

難到會不想知

等冪求和公式在

$\sum \limits_{k = 1}^n k^p = \frac 1 {p + 1} \sum \limits_{i = 0}^p \left({-1}\right)^i \binom {p + 1} i B_i n^{p + 1 - i}$

$= \frac{1}{p+1} \left( \binom {p + 1}0 B_0 n^{p+1} - \binom {p + 1} 1 B_1 n^p + \cdots + \binom {p + 1} {2k} B_{2k} n^{p+1-2k} + \cdots \right)$

，呼喚白努利『多項式』快出來！

Bernoulli polynomials

In mathematics, the Bernoulli polynomials occur in the study of many special functions and in particular the Riemann zeta function and the Hurwitz zeta function. This is in large part because they are an Appell sequence, i.e. a Sheffer sequence for the ordinary derivative operator. Unlike orthogonal polynomials, the Bernoulli polynomials are remarkable in that the number of crossings of the x-axis in the unit interval does not go up as the degree of the polynomials goes up. In the limit of large degree, the Bernoulli polynomials, appropriately scaled, approach the sine and cosine functions.

This article also discusses the Bernoulli polynomials and the related Euler polynomials, and the Bernoulli and Euler numbers.

Bernoulli polynomials

Representations

The Bernoulli polynomials B_n admit a variety of different representations. Which among them should be taken to be the definition may depend on one’s purposes.

Explicit formula

B_n(x) = \sum_{k=0}^n {n \choose k} b_{n-k} x^k,

for n ≥ 0, where b_k are the Bernoulli numbers.

Generating functions

The generating function for the Bernoulli polynomials is

\frac{t e^{xt}}{e^t-1}= \sum_{n=0}^\infty B_n(x) \frac{t^n}{n!}.

The generating function for the Euler polynomials is

\frac{2 e^{xt}}{e^t+1}= \sum_{n=0}^\infty E_n(x) \frac{t^n}{n!}.

Representation by a differential operator

The Bernoulli polynomials are also given by

B_n(x)={D \over e^D -1} x^n

where D = d/dx is differentiation with respect to x and the fraction is expanded as a formal power series. It follows that

\int _a^x B_n (u) ~du = \frac{B_{n+1}(x) - B_{n+1}(a)}{n+1} ~.

cf. integrals below.

Representation by an integral operator

The Bernoulli polynomials are the unique polynomials determined by

\int_x^{x+1} B_n(u)\,du = x^n.

The integral transform

(Tf)(x) = \int_x^{x+1} f(u)\,du

on polynomials f, simply amounts to

</span

This can be used to produce the inversion formulae below.

Explicit expressions for low degrees

The first few Bernoulli polynomials are:

</span

─── 摘自《時間序列︰生成函數‧漸近展開︰白努利 □○《七》》

彼此關係嘛！總是他心通人理同的吧！！

就算不曉誰先用

$\sum \limits_{k=0}^{\infty} B_k (x+1) \frac{t^k}{k!} = \frac{t e^{(x+1)}^t}{e^t -1}$ ，

其目的不可知嗎？

$= \frac{t (e^t - 1 + 1) e^{xt}}{e^t - 1}$

$= t e^t + \frac{t e^{xt}}{e^t - 1}$

$\therefore B_k (x+1) = k \cdot x^{k-1} + B_k (x)$ 。

如是

$B_k (0+1) = k \cdot 0^{k-1} + B_k(0)$

$B_k (1+1) = k \cdot 1^{k-1} + B_k(1)$

$B_k (2+1) = k \cdot 2^{k-1} + B_k(2)$

$\cdots$

$B_k (m+1) = k \cdot m^{k-1} + B_k (m)$ ，

若取 $x, \ 0 \to n$ 、 $k = p+1$ 整數將之代換，加之得

$B_{p+1} (n+1) = (p+1) \cdot \sum \limits_{m=0}^{n} m^n + B_{p+1} (0)$

$= (p+1) \cdot \sum \limits_{m=0}^{n} m^p + B_{p+1}$ 。

因此等冪求和公式可藉白努利多項式表示為

$\sum \limits_{m=0}^{n} m^p = \frac{B_{p+1} (n+1) - B_{p+1}}{p+1}$ 。

樹莓派、樹莓派之學習、樹莓派之教育

時間序列︰生成函數‧漸近展開︰白努利 □○《十左》

2017-04-03 懸鉤子

論語‧《先進》

子路、曾皙、冉有、公西華侍坐。子曰：「以吾一日長乎爾，毋吾以也。居則曰：「不吾知也！』如或知爾，則何以哉？」子路率爾而對曰：「千乘之國，攝乎大國之間，加之以師旅，因之以饑饉；由也為之，比及三年，可使有勇，且知方也。」夫子哂之。「求！爾何如？」對曰：「方六七十，如五六十，求也為之，比及三年，可使足民。如其禮樂，以俟君子。」「赤！爾何如？」對曰：「非曰能之，願學焉。宗廟之事，如會同，端章甫，願為小相焉。」「點！爾何如？」鼓瑟希，鏗爾，舍瑟而作。對曰：「異乎三子者之撰。」子曰：「何傷乎？亦各言其志也。」曰：「莫春者，春服既成。冠者五六人，童子六七人，浴乎沂，風乎舞雩，詠而歸。」夫子喟然歎曰：「吾與點也！」三子者出，曾皙後。曾皙曰：「夫三子者之言何如？」子曰：「亦各言其志也已矣。」曰：「夫子何哂由也？」曰：「為國以禮，其言不讓，是故哂之。」「唯求則非邦也與？」「安見方六七十如五六十而非邦也者？」「唯赤則非邦也與？」「宗廟會同，非諸侯而何？赤也為之小，孰能為之大？」

有說孔子弟子賢人七十二

四科十哲與著名弟子資料

古代尊師-孔子畫像據《史記》記載，孔子有弟子三千，其中精通六藝者七十二人，稱「七十二賢人」。孔子有十位傑出弟子，號稱孔門四科十哲：

在德行方面出眾的有：顏回（顏淵）、閔損（閔子騫）、冉耕（伯牛）、冉雍（仲弓）。在言語方面出眾的有：宰予（宰我）、端木賜（子貢）。在文學方面出眾的有：言偃（子游）、卜商（子夏）。在政事方面出眾的有：冉求（冉有）、仲由（子路）。十哲以外，在文學方面出眾的有顓孫師（子張）、曾參（子輿）、澹臺滅明（子羽）、原憲（子思）、公冶長（子長）、樊須（樊遲）、有若（子有）、公西赤（子華）。

出自《先進篇》。爾時子曰︰

莫春者，春服既成。冠者五六人，童子六七人，浴乎沂，風乎舞雩，詠而歸。

！所以五六得三十，六七得四十二，豈非加之得七十二賢乎？所以黃花岡特記載十二烈士耶？？若說拼湊數字，何數不可得，何況是大中取小也！！此與條條大道通羅馬之道理不可同日而語矣。

不是不可由白努利多項式的定義

$B_n(x) = \sum \limits_{k=0}^{n} \binom {n}k B_k x^{n-k}$ ，直接求導數

$B_n^{'}(x) = \sum \limits_{k=0}^{n} \binom {n}k (n-k) B_k x^{n-k-1}$

$= \sum \limits_{k=0}^{n-1} \binom {n}k (n-k) B_k x^{n-k-1}$

$= \sum \limits_{k=0}^{n-1} \frac{n!}{k! (n-k)!} (n-k) B_k x^{n-k-1}$

$= \sum \limits_{k=0}^{n-1} n \cdot \frac{(n-1)!}{k! (n-k-1)!} B_k x^{n-1-k}$

$= n \cdot \sum \limits_{k=0}^{n-1} \binom {n-1}k B_k x^{n-1-k}$

$= n B_{n-1} (x)$ 。

不過是強調生成函數之應用法而已。

假使將 $x^m$ 改寫成

$= {\left( \frac{1}{2} + (x - \frac{1}{2}) \right)}^m$ ，那麼依據二項式定理

$= \sum \limits_{k=0}^m \binom {m}k {(\frac{1}{2})}^{m-k} {(x - \frac{1}{2} )}^k$ 。

所以 $B_n (x)$ 當然可用 ${(x - \frac{1}{2})}^m$ 作級數展開哩。

熟悉二項式係數恆等式者︰

有關二項式係數的恆等式

關係式

階乘公式能聯繫相鄰的二項式係數，例如在k是正整數時，對任意n有：

${\binom {n+1}{k}}={\binom {n}{k}}+{\binom {n}{k-1}}$
$\binom{n}{k} = \frac{n}{k} \binom{n-1}{k-1}$
$\binom {n-1}{k} - \binom{n-1}{k-1} = \frac{n-2k}{n} \binom{n}{k}.$

兩個組合數相乘可作變換：

\binom ni \binom im=\binom nm \binom {n-m}{i-m}

^{[參 2]}

一階求和公式

$\sum_{r=0}^n \binom nr = 2^{n}$
$\sum _{r=0}^{k}{\binom {n+r-1}{r}}={\binom {n+k}{k}}$
$\sum _{r=0}^{n-k}{\frac {(-1)^{r}(n+1)}{k+r+1}}{\binom {n-k}{r}}={\binom {n}{k}}^{-1}$
$\sum_{r=0}^n \binom {dn}{dr}=\frac{1}{d}\sum_{r=1}^d (1+e^{\frac{2 \pi r i}{d}})^{dn}$ ^{[參 3]}
$\sum _{r=0}^{n}r^{m}{\binom {n}{r}}=n(n+1)\cdots (n+m-1)2^{n-m}$

(1+e^{x})^{n}=\sum _{{r=0}}^{n}e^{{rx}}{\binom {n}{r}}

n(n-1)\cdots (n-m+1)(1+e^{0})^{{n-m}}=\sum _{{r=0}}^{n}r^{m}e^{0}{\binom {n}{r}}

$\sum_{i=m}^n \binom {a+i}{i} = \binom {a+n+1}{n} - \binom {a+m}{m-1}$

\binom {a+m}{m-1} + \binom {a+m}{m} + \binom {a+m+1}{m+1} + ... + \binom {a+n}{n} = \binom {a+n+1}{n}

$F_n=\sum_{i=0}^{\infty} \binom {n-i}{i}$ ^{[參 4]}

F_{n-1}+F_n=\sum_{i=0}^{\infty} \binom {n-1-i}{i}+\sum_{i=0}^{\infty} \binom {n-i}{i}=1+\sum_{i=1}^{\infty} \binom {n-i}{i-1}+\sum_{i=1}^{\infty} \binom {n-i}{i}=1+\sum_{i=1}^{\infty} \binom {n+1-i}{i}=\sum_{i=0}^{\infty} \binom {n+1-i}{i}=F_{n+1}

主條目：朱世傑恆等式

$\sum_{i=m}^n \binom ia = \binom {n+1}{a+1} - \binom {m}{a+1}$

\binom {m}{a+1} + \binom ma + \binom {m+1}a ... + \binom na = \binom {n+1}{a+1}

二階求和公式

$\sum _{r=0}^{n}{\binom {n}{r}}^{2}={\binom {2n}{n}}$
$\sum_{i=0}^n \binom {r_1+n-1-i}{r_1-1} \binom {r_2+i-1}{r_2-1}=\binom {r_1+r_2+n-1}{r_1+r_2-1}$ ^{[參 5]}

(1-x)^{-r_1} (1-x)^{-r_2}=(1-x)^{-r_1-r_2}

(1-x)^{-r_1} (1-x)^{-r_2}=(\sum_{n=0}^{\infty} \binom {r_1+n-1}{r_1-1} x^n)(\sum_{n=0}^{\infty} \binom {r_2+n-1}{r_2-1} x^n)=\sum_{n=0}^{\infty} (\sum_{i=0}^n \binom {r_1+n-1-i}{r_1-1} \binom {r_2+i-1}{r_2-1}) x^n

(1-x)^{-r_1-r_2}=\sum_{n=0}^{\infty} \binom {r_1+r_2+n-1}{r_1+r_2-1} x^n

主條目：范德蒙恆等式

$\sum_{i=0}^k \binom ni \binom m{k-i}=\binom {n+m}k$

三階求和公式

主條目：李善蘭恆等式

${\binom {n+k}k}^2=\sum_{j=0}^k {\binom kj}^2 \binom {n+2k-j}{2k}$

應能將此展開式簡化吧☆

樹莓派、樹莓派之學習、樹莓派之教育

時間序列︰生成函數‧漸近展開︰白努利 □○《十前》

2017-04-02 懸鉤子

樂府古題要解
作者：吳兢‧唐

舊本題唐吳兢撰。兢有《貞觀政要》，已著錄。考《崇文總目》載《古樂府古題要解》共十二卷。晁公武《讀書志》稱兢纂采漢、魏以來古樂府詞凡十卷。又於傳記及諸家文集中采樂府所起本義，以釋解古題。觀《崇文總目》稱二書共十二卷，而《讀書志》稱古樂府十卷，則所餘二卷為《樂府古題要解》矣。卷數與今本相合。《崇文總目》又載《樂府解題》，稱不著撰人名氏。與吳兢所撰《樂府古題》頗同，以《江南曲》為首。其後所解差異。此本為毛晉津逮秘書所刊。後有晉跋，稱今人以兢所撰與《樂府解題》混為一書。又稱太原郭氏諸敘中，輒引《樂府解題》不及《古題要解》。今考郭茂倩《樂府詩集》所引《樂府解題》，自漢鐃歌《上之回》篇始，乃明題吳兢之名。則混為一書，已不始於近代。然茂倩所引，其文則與此書全同，不過偶刪一二句，或增入樂府本詞一二句，不應互相剿襲至此。疑兢書久佚，好事者因《崇文總目》有「《樂府解題》與吳兢所撰樂府頗同」語，因捃拾郭茂倩所引《樂府解題》，偽為兢書。而不知王堯臣等所謂與樂府頗同者，乃指其解說古題體例相近，非謂其文全同。觀下文即雲以《江南曲》為首，其後所解差異，是二書不同之明證。安有兩家之書如出一口者乎？且樂府自樂府，雜詩自雜詩，卷末乃載及建除諸體，並及於字謎之類，其為捃拾以足兩卷之數，灼然可知矣。《晉跋》稱是書凡三本，一得之廣山楊氏，一得之錫山顏氏，最後乃得一元板。然則是書為元人所贗造也。

序

樂府之興，肇於漢魏。歷代文士，篇詠實繁。或不睹於本章，便斷題取義。贈夫利涉，則述《公無度河》；慶彼載誕，乃引《烏生八九子》；賦雉斑者，但美繡錦臆；歌天馬者，唯敘驕馳亂蹋。類皆若茲，不可勝載。遞相祖習，積用為常，欲令後生，何以取正？余頃因涉閱傳記，用諸家文集，每有所得，輒疏記之。歲月積深，以成卷軸，向編次之，目為《古題要解》雲爾。

水仙操

右：舊說伯牙學鼓琴於成連先生，三年而成。至於精神寂寞，情誌專一，尚未能也。成連雲『吾理由子春在海中，能移人情。』乃與伯牙延望，無人。至蓬萊山，留伯牙曰：『吾將迎吾師。』刺船而去，旬時不返，但聞海上水汩汲漰澌之聲。山林窅冥，群鳥悲號，愴然嘆曰：『先生將移我情。』乃援琴而歌之。曲終，成連刺船而還。伯牙遂為天下妙手。

歇後語說︰水仙不開花，裝蒜。貌似未必真，贗造常是假。思想起伯牙和鍾子期，可能世上知音希。因著歐拉求和公式註釋多！於是暫且放下克萊因先生文字註釋？與其左右為難，又不能照顧前後？不如先回到白努利多項式基本性質的了？！

假設 $B_n(x)$ 為白努利多項式，那麼依定義

$B_n(x) = \sum \limits_{k=0}^{n} \binom {n}k B_k x^{n-k}$ 。

已求過 $B_n(x)$ 之生成函數為

$\frac{t e^{xt}}{e^t -1} = \sum \limits_{k=0}^{\infty} B_k (x) \frac{t^k}{k!} \ \ \ \ \ (1)$ 。

將 $(1)$ 式兩邊對 $x$ 微分，右邊得

$\sum \limits_{k=0}^{\infty} B_k^{'} (x) \frac{t^k}{k!}$ ，由於

$\lim \limits_{t \to 0} \frac{t e^{xt}}{e^t -1} = 1 = B_0 (x)$ ，所以

$B_0^{'} (x) = 0$ ，因此右邊可寫成

$\sum \limits_{k=1}^{\infty} B_k^{'} (x) \frac{t^k}{k!}$ 。左邊得

${\left( \frac{t e^{xt}}{e^t -1} \right)}^{'} = \frac{t^2 e^{xt}}{e^t -1} = t \times \frac{t e^{xt}}{e^t -1}$

$= t \times \sum \limits_{k=0}^{\infty} B_k (x) \frac{t^k}{k!}$

$= \sum \limits_{k=0}^{\infty} B_k (x) \frac{t^{k+1}}{k!}$

$= \sum \limits_{k=1}^{\infty} B_{k-1} (x) \frac{t^k}{(k-1)!}$

$\therefore \frac{B_k^{'} (x)}{k!} = \frac{B_{k-1} (x)}{(k-1)!}$ 。故得

$B_k^{'} (x) = k \cdot B_{k-1} (x), \ k \ge 1$ ☆

此 $k$ 描述無窮白努利多項式間前後兩者之關係，實不同於某有既定關係函數序列 $y_n = A \cdot {(x + \alpha)}^n$ ， $y_n = (x+\alpha) \cdot y_{n-1}$ 。

若因剛好 $\frac{d y_n}{dx} = n \left( A {(x + \alpha)}^{n-1} \right) = n \cdot y_{n-1}$ ，如是就以為如果 $y_0 = 1$ ，那麼 $A=1$ ，要是 $y_1 = x - \frac{1}{2}$ ，那麼 $\alpha = - \frac{1}{2}$ ，得到了 $y_n = {(x-\frac{1}{2})}^n$ ，當真是白努利多項式耶？？豈不會陷於淺盤深水乎！！

此所以有人講『陰影微積分』夫？？！！

Umbral calculus

In mathematics before the 1970s, the term umbral calculus referred to the surprising similarity between seemingly unrelated polynomial equations and certain shadowy techniques used to ‘prove’ them. These techniques were introduced by John Blissard (1861) and are sometimes called Blissard’s symbolic method. They are often attributed to Édouard Lucas (or James Joseph Sylvester), who used the technique extensively.^[1]

In the 1930s and 1940s, Eric Temple Bell attempted to set the umbral calculus on a rigorous footing.

In the 1970s, Steven Roman, Gian-Carlo Rota, and others developed the umbral calculus by means of linear functionals on spaces of polynomials. Currently, umbral calculus refers to the study of Sheffer sequences, including polynomial sequences of binomial type and Appell sequences, but may encompass in its penumbra systematic correspondence techniques of the calculus of finite differences.

The 19th-century umbral calculus

The method is a notational procedure used for deriving identities involving indexed sequences of numbers by pretending that the indices are exponents. Construed literally, it is absurd, and yet it is successful: identities derived via the umbral calculus can also be properly derived by more complicated methods that can be taken literally without logical difficulty.

An example involves the Bernoulli polynomials. Consider, for example, the ordinary binomial expansion (which contains a binomial coefficient):

(y+x)^{n}=\sum _{{k=0}}^{n}{n \choose k}y^{{n-k}}x^{k}

and the remarkably similar-looking relation on the Bernoulli polynomials:

B_{n}(y+x)=\sum _{{k=0}}^{n}{n \choose k}B_{{n-k}}(y)x^{k}.

Compare also the ordinary derivative

{\frac {d}{dx}}x^{n}=nx^{{n-1}}

to a very similar-looking relation on the Bernoulli polynomials:

{\frac {d}{dx}}B_{n}(x)=nB_{{n-1}}(x).

These similarities allow one to construct umbral proofs, which, on the surface, cannot be correct, but seem to work anyway. Thus, for example, by pretending that the subscript n − k is an exponent:

B_{n}(x)=\sum _{{k=0}}^{n}{n \choose k}b^{{n-k}}x^{k}=(b+x)^{n},

and then differentiating, one gets the desired result:

B_{n}'(x)=n(b+x)^{{n-1}}=nB_{{n-1}}(x).\,

In the above, the variable b is an “umbra” (Latin for shadow).

□ ＝ ○ ‧ ☆☆

2017-04-01 懸鉤子

搖搖頭 ↑
揮揮手 →
頗多愁 ↓
快快溜 α
慢慢走 ω

ㄡㄡ
愚人節到嘍 ←

日	一	二	三	四	五	六
« 3 月				5 月 »
						1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28	29
30

FreeSandal

每月彙整: 2017 年 4 月

時間序列︰生成函數‧漸近展開︰白努利 □○《十右》

Symmetry

蕩寇志

時間序列︰生成函數‧漸近展開︰白努利 □○《十中》

Theorem

Bernoulli polynomials

Representations

Explicit formula

Generating functions

Representation by a differential operator

Representation by an integral operator

Explicit expressions for low degrees

時間序列︰生成函數‧漸近展開︰白努利 □○《十左》

四科十哲與著名弟子資料

有關二項式係數的恆等式

關係式

一階求和公式

二階求和公式

三階求和公式

時間序列︰生成函數‧漸近展開︰白努利 □○《十前》

Umbral calculus

The 19th-century umbral calculus

□ ＝ ○ ‧ ☆☆

輕。鬆。學。部落客