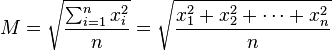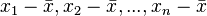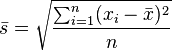為了談談『量測』的『數據分析』,就讓我們從一些常用『術語』開始 。假使量測某一物理量 ![]() 次,得到
次,得到 ![]() 個測量值
個測量值
![]() ,所謂的
,所謂的
【算術平均值】等於
![]()
【偏差】deviation 定義為任一個量測數據與整體算術平均值之差。因此偏差值有正有負,整組數據的偏差值總和為零。如果用 ![]() 表示
表示 ![]() 的偏差值,那麼
的偏差值,那麼 ![]() 而且
而且 ![]() 。
。
【平均偏差】定義為︰所有偏差之『絕對值』的『算術平均值』。
等於 ![]() 。
。
這個『偏差』的概念,是說假使絕大多數的『量測值』都離『平均值』不遠,因此『平均偏差值』很小,如此可以講此『度量儀器』之『精密度』很高,若是對照
《失之豪釐,差以千里!!《下》》文本︰
若是能解『武功』有所謂『內功』與『外功』,『內功』也就是『練功』之『心法』,由通達『此功』『是什麼』到『為什麼』,『外功』就是『此功』的『 Know How』,大概『內外兼修』之事『思過半矣』的吧。
所以打算應用『感測器』 Sensors 於『 IoT 』的人,自然『需要』 Need To 了解『量測』這『事務』,才容易達成『想要』 Want to 的那『東西』。有關『誤差』之基本『觀念』,以及『數據處理』的一般『方法』,讀者可以閱讀
一文多作理解。作者不過『杯水車薪』,徒擔心測『杯水』怕那『儀器』不夠『靈敏』,用『秤坨』量『車薪』恐是『操作』不當 ,也只能『杯水車薪』點滴一番,起個薪火罷了。
尤其注意
【篩選數據者之誤】
一九七四年美國大物理學家理查‧費曼 Richard Phillips Feynman 曾經在『加州理工學院』 California Institute of Technology 的一場畢業典禮演說當中述說『草包族科學』Cargo cult science,他其中有一段講:
從過往的經驗,我們學到了如何應付一些自我欺騙的情況。舉個例子,密立根做了個油滴實驗,量出了電子的帶電量,得到一個今天我們知道是不大對的答案。他的資料有點偏差,因爲他用了個不準確的空氣粘滯係數數值。於是,如果你把在密立根之後、進行測量電子帶電量所得到的資料整理一下,就會發現一些很有趣的現象: 把這些資料跟時間畫成座標圖,你會發現這個人得到的數值比密立根的數值大一點點,下一個人得到的資料又再大一點點,下一個又再大上一點點,最後,到了一個 更大的數值才穩定下來。
為 什麼他們沒有在一開始就發現新數值應該較高?── 這件事令許多相關的科學家慚愧臉紅 ── 因爲顯然很多人的做事方式是:當他們獲得一個比密立根數值更高的結果時,他們以爲一定哪裡出了錯,他們會拚命尋找,並且找到了實驗有錯誤的原因。另一方面,當他們獲得的結果跟密立 根的相仿時,便不會那麼用心去檢討。因此,他們排除了所謂相差太大的資料,不予考慮。我們現在已經很清楚那些伎倆了,因此再也不會犯同樣的毛病。
更需小心
【準確與精密】
概念之區分。
引自維基百科︰
『準確度』 Accuracy 與『精密度』 Precision 是在科學、工程學、工業及統計學等範疇上一個重要概念。
準確度是每一次獨立的測量之間,其平均值與已知的數據真值之間的差距(與理論值相符合的程度)。例如:多次實驗結果其平均值接近於已知的數據真值(理論值),可知道數據「準確」,或是數據具有「高準確度」;反之,平均值與已知的數據真值差距較大,表示實驗數據不準確,或準確度不高。
精密則是當實驗數據很精準時,會要求實驗有高度的再現性,表示實驗數據是可信的,也就是實驗數據需要具有高精密度。(多次量度或計算的結果的一致程度)。
一個結果必須要同時符合『準確』與『精密』這兩個條件,才可算是『精準』。
常 見文獻以射擊彈著點分佈情形來說明準確度與精密度的意義如圖示,初看似乎簡明易懂,實際仍隱含認知的盲點。以射擊而言每一彈著點均儘量接近靶心才稱得上精 確或是精準;最左邊圖示就一般射擊而言屬於低準確度低精密度。如果是期望求得彈道與瞄準機制間的關係、以槍隻調校為目的的射擊,其本質與一般真值未知的測 量或實驗相同,同一最左邊圖示因為彈著點分佈其平均值接近靶心,依準確度的定義則屬於高準確度低精密度。
『中的』,距離『目標』多遠,決定『準確性』;『密集』,『各次』的『結果』彼此『相近』,確立『精密度』 。既『中的』又『密集』,才是『量測』之『精準儀器』。
───
或將更能清楚明白耶!!
【標準偏差】 standard deviation 定義為︰偏差之均方根。等於
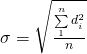 。
。
這個『標準差』概念的『統計意義』,當可以由網文︰
- 通常當 測量次數多時,測量數據的 隨機分佈 滿足
- 常態分佈 (normal or gaussian distribution):

P 是測量值 為 x 的機率。(次數少時為二項式分佈)。
如下圖為平均值為 50, 標準差為 10. 的常態分佈,

測量值 出現在
![]() 範圍內的機率為 68.3% 。(2:1)
範圍內的機率為 68.3% 。(2:1)
![]() 範圍內的機率為 95.4%。(20:1)
範圍內的機率為 95.4%。(20:1)
![]() 範圍內的機率為 99.7%。(350:1)
範圍內的機率為 99.7%。(350:1)
![]() 範圍內的機率為 99.994%。(15000:1)
範圍內的機率為 99.994%。(15000:1)
───
知其『機率』之意指。如果針對『感測器』,或者說『物理量測』而言,最好能夠明瞭『標準差』的『物理意義』︰
之前在《【Sonic π】電路學之補充《二》》一篇裡,我們說到了『平均功率』的『定義』,通常物理上與工程中常用『均方根』或叫做『平方平均數』 Root mean square 來計算這個『平均值』,就讓先我們將『平均功率』的定義引述於此
所謂的『功率』 power 是指『能量』之『轉換』或者『使用』的『速率』,用單位時間的能量大小來表示。『功率』的『單位』是『瓦特』 W ,假使 ![]() 是一物理系統在
是一物理系統在 ![]() 時間內所做的功,那麼這段時間內的『平均功率』
時間內所做的功,那麼這段時間內的『平均功率』 ![]() 可以由下式給出
可以由下式給出
![]()
。而『瞬時功率』就是當時間 ![]() 時,『平均功率』的極限值
時,『平均功率』的極限值
![]()
。也就是講一秒消耗一焦耳的能量就是一『瓦特』,一般所說的『一度電』是指『一千瓦小時』所使用的『電能』多寡,它等於 ![]() 。
。
從『瞬時功率』 的『定義』,可以推導出
【機械瞬時功率】是 ![]() ;
;
【電力瞬時功率】是 ![]()
。 那麽『均方根』 ![]() 的『定義』就是,如果在
的『定義』就是,如果在 ![]() 到
到 ![]() 時距中,我們『度量』了某個
時距中,我們『度量』了某個 ![]() 『物理量』
『物理量』 ![]() 次
次 ![]() ,這個『物理量』的『量測值』是
,這個『物理量』的『量測值』是 ![]() ,這時我們說這個『物理量』
,這時我們說這個『物理量』 ![]() 的『均方根』
的『均方根』 ![]() 是
是
![]()
。也可以說,對於一個『連續』可『度量』的 ![]() 而言﹐它就是
而言﹐它就是
![]()
,設使 ![]() 只存在於
只存在於 ![]() 至
至 ![]() 時距間,此時 『均方根』 是
時距間,此時 『均方根』 是
![]() 。
。
為什麼是這樣『定義』的呢?假使我們『預期』一個『刺激源』是『周期函數』,它的『響應』也就會是一個『同頻率』之『周期函數』,如此只需要知道『一個週期』的『現象』,就能夠推論『任意時間』的『結果』。更何況『傅立葉分析』讓我們能推廣到更複雜的狀況,即使是『刺激源』根本就不是個『周期函數』的情形。如果從物理上來說,這個『均方表述』就是滿足『線性』、『疊加原理』與『熱力平衡』種種為『特徵』的『描述』,或許講,是人們常用『習知』之『標準差』的啊!!
─── 引自《【Sonic π】電聲學之電路學《一》下》
所謂『平方平均數』是指︰
平方平均數(Quadratic mean),簡稱均方根(Root Mean Square,縮寫為 RMS),是 2 次方的廣義平均數的表達式,也可叫做 2 次冪平均數。其計算公式是:
在連續函數 的區間
的區間![\begin{smallmatrix}[a,b]\end{smallmatrix}](https://upload.wikimedia.org/math/0/2/c/02c2d84980612324d0b93ba4caebe459.png) 內,其均方根定義為:
內,其均方根定義為:
![f_{\mathrm{rms}} = \sqrt {{1 \over {b-a}} {\int_{a}^{b} {[f(x)]}^2\, dx}}](https://upload.wikimedia.org/math/6/a/f/6af8508ff0c5072f3fb6695b669b0ab8.png)
應用
方均根常用來計算一組數據和某個數據的「平均差」。像交流電的電壓、電流數值以及均勻加速直綫運動的位移中點平均速度,都是以其實際數值的方均根表示。例如「220V交流電」表示電壓信號的均方根(又稱為有效值)為 220V,為交流電瞬時值(瞬時值又稱暫態值)的最大值(峰值)的 。
。
另外,統計學中的標準差  ,就是所有數據
,就是所有數據  和平均值
和平均值 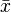 相減後的數據
相減後的數據
的方均根
或將理解『度量』之『交互作用』所引起的『物質』、『能量』、『熱量』… 之變化乎??