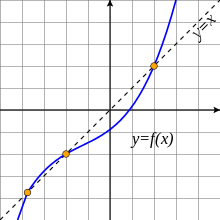
□ ○ 變動中或有『不變』之處,就函數而言稱之為『不動點』,也叫做『定點』︰
美國著名的哲學、邏輯學家 Willard Van Orman Quine 曾經提過一個非自我指涉的真假值『悖論』︰
“Yields falsehood when preceded by its quotation” yields falsehood when preceded by its quotation.
,或許可以用下面的中文例子比擬如下︰
“引用生虛假”引用生虛假。
那這句話是『真』還是『假』呢?假使這樣分解的看︰
□ = 引用生虛假
□ 的引用 = “引用生虛假”
□ 的引用之引用生虛假 = “引用生虛假”引用生虛假
『引用生虛假』引用生『虛假』,所以 “□” □ 自相矛盾。
一九七二年 Paul Bratley 和 Jean Millo 寫了一篇《Computer Recreations: Self-Reproducing Automata》技術文章,『自我再現』一詞首度出現,是指一種無需輸入,『自己輸出自己原始碼』的執行程式,也就是說『執行程式○的輸出=程式○的原始碼』。據說一九六零年 Bratley 在 Edinburgh 大學的一場由該校研究員 Hamish Dear 的演講會上,第一次看到用了 Atlas Autocod 寫的此種程式時,就對它產生了興趣。人們後來為了紀念哲學家奎因,就將這類程式稱作『Quine』程式。通常在任何圖零 Turing 完備的程式語言上,都可以寫出 Quine 程式,這個網址列出了許多種程式語言的寫作範例。有人說,它的一般的寫法是︰
一、程式原始碼的資料結構,
二、輸出該資料結構,
三、用該資料結構之內容輸出其餘的程式原始碼。
比方說下面是一個 python 語言的簡單例子︰
a = [ ‘print “a =”, a’, ‘for s in a: print s’]
print “a =”, a
for s in a: print s
甚至 Laurent Vogel 用 Thue 語言寫了一個 Quine 的程式,有興趣的讀者可以到他的網站下載程式,好好研究一下︰
_x00::=2210001112000100020120000112200210220120211220221000110×01
>0::=0>~00
_2::=_~2
_x01::=22100021120011001201200011112020200101222011220221000210×02
>1::=1>~01
~220::=~_
_x02::=221010011200210022012000211012110210111220221010010×10
>2::=2>~02
1<::=<1
_x10::=221010111022110210211221211022120220112200010220120011220221010110×11
2<::=<2
x<::=x>_
_0::=_~0
_x11::=221010211220011022012011100211021001112000010120011220221010210×12
_1::=_~1
0<::=<0
~00::=~0
_x12::=221020011120001101201111200021012021112010010121011220221020010×20
~01::=~1
~02::=~2
~10::=~::=
_x20::=2210201111201011012111201021012121112020010122011220221020110×21
~11::=~
~12::=~~
~20::=~>
_x21::=2210202112022110212211112020110122111220221020210×22
>x::=<x
~21::=~<
_x22::=2211112020201101222111101122120220020200020201000000000100221000011x
~221::=~x
::=
x>_220221000010x00
這個『自我再現』和『定點』fixed point 的概念是息息相關的,在此從數學的角度上來講,假使有一個數值函數 ![]() ,那它的定點的定義是︰
,那它的定點的定義是︰
![]()
,假使有一個滿足這個方程式的數值 ![]() ,從定義可知
,從定義可知 ![]() ,由此可知在『迭代』或『遞迴』計算的『終止條件』考慮上十分的重要,它在不同的領域裡有多個『定理』以及很多的『應用』。
,由此可知在『迭代』或『遞迴』計算的『終止條件』考慮上十分的重要,它在不同的領域裡有多個『定理』以及很多的『應用』。
─── 摘自《自我再現 ── Thue 改寫系統之補充《三》》
這常令人感覺奇妙,卻又彰顯事物內蘊也!
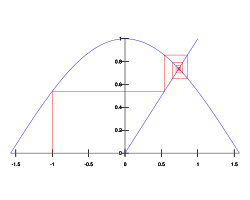
試想『透視』函數 ![]() 有『定點』乎?
有『定點』乎?
設有 ![]() 兩線,而且
兩線,而且 ![]() 與
與 ![]() 是那兩線上共線和對應之三點。已知
是那兩線上共線和對應之三點。已知 ![]() ,那麼這兩線之間形成透視關係,同時滿足『分式線性變換』形式。
,那麼這兩線之間形成透視關係,同時滿足『分式線性變換』形式。

可得
![]()
![]() 也。
也。
不求解能否知道 ![]() 與
與 ![]() 兩線之『交點』必是『定點』呢??
兩線之『交點』必是『定點』呢??
已求解
pi@raspberrypi:~0
\frac{-\alpha \beta z_1 + \alpha z_1 + \alpha \beta z_2 - \beta z_2}{\alpha - \beta}
\frac{-\alpha \beta z_1 + \alpha z_1 + \alpha \beta z_2 - \beta z_2}{\alpha - \beta}
= \frac{(-\alpha \beta + \alpha)z_1 + (\alpha \beta -\beta)z_2}{\alpha - \beta}, \ \frac{-\alpha \beta + \alpha}{\alpha - \beta} + \frac{\alpha \beta -\beta}{\alpha - \beta} = 1
= \frac{(- \beta + 1)\alpha z_1 + (\alpha - 1)\beta z_2}{\alpha - \beta}, \ \frac{- \beta + 1}{\alpha - \beta} + \frac{\alpha - 1}{\alpha - \beta} = 1
p
{z_1}^{'} - p = \alpha (z_1 - p), \ {z_2}^{'} - p = \beta (z_2 - p) \ z^{'} - p = \gamma (z - p)
z^{'} = p+ \frac{\alpha \cdot \beta \cdot (z-p) \cdot (z_2-z_1) }{\alpha ( z -z_1) - \beta (z -z_2)}$ 。 且再驗證求解一番︰
In [8]: p = symbols('p') In [9]: p點透視 = (α*β*(z2-z1)*(z-p))/(α*(z-z1)-β*(z-z2)) + p In [10]: (p點透視.subs(z, z1)).simplify() Out[10]: p - α⋅(p - z₁) In [11]: (p點透視.subs(z, z2)).simplify() Out[11]: p - β⋅(p - z₂) In [12]: p定點 = solve(z - p點透視, z) In [13]: p定點 Out[13]: ⎡ ______________________________ ⎢ ╱ ⎢p⋅α - p⋅β - z₁⋅α⋅β + z₁⋅α + z₂⋅α⋅β - z₂⋅β - ╲╱ (p⋅α - p⋅β + z₁⋅α⋅β - z₁⋅α - ⎢───────────────────────────────────────────────────────────────────────────── ⎣ 2⋅(α - β) ________________ _____________ 2 ╱ z₂⋅α⋅β + z₂⋅β) p⋅α - p⋅β - z₁⋅α⋅β + z₁⋅α + z₂⋅α⋅β - z₂⋅β + ╲╱ (p⋅α - p⋅β + ────────────────, ──────────────────────────────────────────────────────────── 2⋅(α - β) _________________________________⎤ 2 ⎥ z₁⋅α⋅β - z₁⋅α - z₂⋅α⋅β + z₂⋅β) ⎥ ─────────────────────────────────⎥ ⎦ In [14]:
,此刻需要自己協助 SymPy 簡化根號未盡之功哩??!!將得到『p定點[1] = p』、『p定點[0] = l 與 l' 交點』呦!!??
故知『點』『線』間之『重合關係』亦不容易勒◎
重合幾何
在數學裡,重合幾何(incidence geometry)是研究重合結構的一門學科。歐氏平面之類的幾何是一個複雜的數學物件,包含長度、角度、連續性、中間性與重合關係。 當其他的概念都被去掉,剩下的就只有「重合結構」,有關哪個點會位於哪條線上的資訊。即使有這樣嚴格的限制,還是有定理可被證明,而且存在著與此一結構有 關之有趣事實。這樣的基本結論在其他概念被加回來形成較豐富的幾何時,仍然有效。有時,一些作者會搞混研究與研究的物件之間的不同之處,所以有些作者會將 重合結構指為重合幾何,這並不令人意外[1]。
重合結構會自然地出現於各個不同的數學領域之內,並已被許多人研究過。因此,存在著許多不同的詞彙用來描述此一物件。在圖論裡,重合結構被稱為超圖;而在組合設計理論裡,則被稱為區塊設計。 除了詞彙的不同外,每個領域也以不同的方式處理此一物件,並對這些物件與該學科有關的一類問題感興趣。使用幾何的語言,如同在重合幾何內一般,形狀即時常 會被作為主題與範例。不過,將其中一個學科裡的結論轉換成另一學科裡的用詞是可能的,雖然這往往會導致難以操作且令人費解的陳述,不像是該主題原本的一部 分。在本條目裡,只會選擇使用能自然呈現幾何語言的範例。
其中最令人感興趣的例子為在歐氏平面上的有限點集合,可由重合結構決定線的數量與類型。因為只考慮重合性質,上述情形所得之部分結論可延伸至更一般的設定上。
Incidence structure
In mathematics, an abstract system consisting of two types of objects and a single relationship between these types of objects is called an incidence structure. Consider the points and lines of the Euclidean plane as the two types of objects and ignore all the properties of this geometry except for the relation of which points are on which lines for all points and lines. What is left is the incidence structure of the Euclidean plane.
Incidence structures are most often considered in the geometrical context where they are abstracted from, and hence generalize, planes (such as affine, projective, and Möbius planes), but the concept is very broad and not limited to geometric settings. Even in a geometric setting, incidence structures are not limited to just points and lines; higher-dimensional objects (planes, solids, n-spaces, conics, etc.) can be used. The study of finite structures is sometimes called finite geometry.[1]
In geometry, the Möbius–Kantor configuration is a configuration consisting of eight points and eight lines, with three points on each line and three lines through each point. It is not possible to draw points and lines having this pattern of incidences in the Euclidean plane, but it is possible in the complex projective plane.
Partial linear spaces
Incidence structures that are most studied are those that satisfy some additional properties (axioms), such as projective planes, affine planes, generalized polygons, partial geometries and near polygons. Very general incidence structures can be obtained by imposing "mild" conditions, such as:
A partial linear space is an incidence structure for which the following axioms are true:[3]
- Every pair of distinct points determines at most one line.
- Every line contains at least two distinct points.
In a partial linear space it is also true that every pair of distinct lines meet in at most one point. This statement does not have to be assumed as it is readily proved from axiom one above.
Further constraints are provided by the regularity conditions:
RLk: Each line is incident with the same number of points. If finite this number is often denoted by k.
RPr: Each point is incident with the same number of lines. If finite this number is often denoted by r.
The second axiom of a partial linear space implies that k > 1. Neither regularity condition implies the other, so it has to be assumed that r > 1.
A finite partial linear space satisfying both regularity conditions with k, r > 1 is called a tactical configuration.[4] Some authors refer to these simply as configurations,[5] or projective configurations.[6] If a tactical configuration has n points and m lines, then, by double counting the flags, the relationship nr = mk is established. A common notation refers to (nr, mk)-configurations. In the special case where n = m (and hence, r = k) the notation (nk, nk) is often simply written as (nk).
A linear space is a partial linear space such that:[7]
- Every pair of distinct points determines exactly one line.
Some authors add a "non-degeneracy" (or "non-triviality") axiom to the definition of a (partial) linear space, such as:
- There exist at least two distinct lines.[8]
This is used to rule out some very small examples (mainly when the sets P or L have fewer than two elements) that would normally be exceptions to general statements made about the incidence structures. An alternative to adding the axiom is to refer to incidence structures that do not satisfy the axiom as being trivial and those that do as non-trivial.
Each non-trivial linear space contains at least three points and three lines, so the simplest non-trivial linear space that can exist is a triangle.
A linear space having at least three points on every line is a Sylvester–Gallai design.

Simplest non-trivial linear space

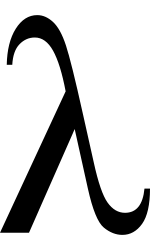
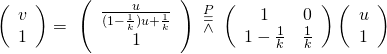 或
或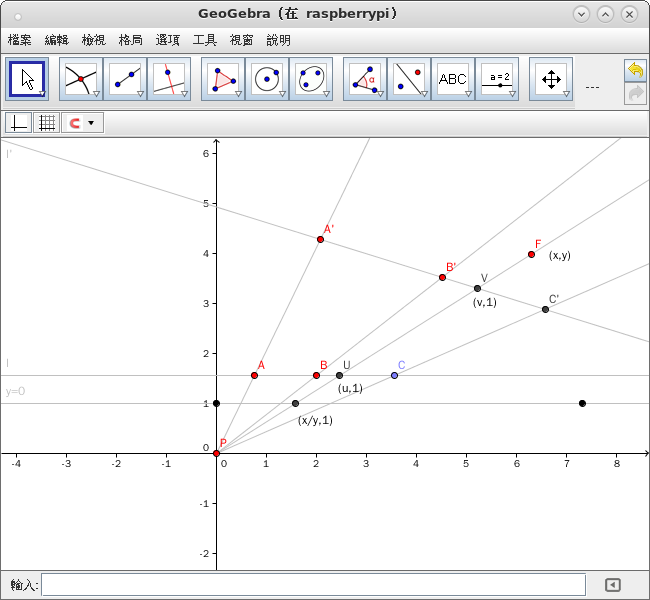
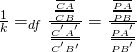 。
。
![Rendered by QuickLaTeX.com ipython3 Python 3.4.2 (default, Oct 19 2014, 13:31:11) Type "copyright", "credits" or "license" for more information. IPython 2.3.0 -- An enhanced Interactive Python. ? -> Introduction and overview of IPython's features. %quickref -> Quick reference. help -> Python's own help system. object? -> Details about 'object', use 'object??' for extra details. In [1]: from sympy import * In [2]: init_printing() In [3]: α , β , z1, z2, z = symbols('α , β , z1, z2, z') In [4]: 分母平移 = Matrix([[1,(β * z2 - α * z1)/(α - β)],[0,1]]) In [5]: 分母平移 Out[5]: ⎡ -z₁⋅α + z₂⋅β⎤ ⎢1 ────────────⎥ ⎢ α - β ⎥ ⎢ ⎥ ⎣0 1 ⎦ In [6]: 反演 = Matrix([[0,1],[1,0]]) In [7]: 反演 Out[7]: ⎡0 1⎤ ⎢ ⎥ ⎣1 0⎦ In [8]: 旋轉縮放 = Matrix([[-(α*β*(z2-z1)*(β*z2-α*z1))/((α-β)**2),0],[0,1]]) In [9]: 旋轉縮放 Out[9]: ⎡-α⋅β⋅(-z₁ + z₂)⋅(-z₁⋅α + z₂⋅β) ⎤ ⎢─────────────────────────────── 0⎥ ⎢ 2 ⎥ ⎢ (α - β) ⎥ ⎢ ⎥ ⎣ 0 1⎦ In [10]: 分子平移 = Matrix([[1,(α*β*(z2-z1))/(α-β)],[0,1]]) In [11]: 分子平移 Out[11]: ⎡ α⋅β⋅(-z₁ + z₂)⎤ ⎢1 ──────────────⎥ ⎢ α - β ⎥ ⎢ ⎥ ⎣0 1 ⎦ In [12]: 透視 = 分子平移*旋轉縮放*反演*分母平移 In [13]: 透視 Out[13]: ⎡α⋅β⋅(-z₁ + z₂) ⎤ ⎢────────────── 0 ⎥ ⎢ α - β ⎥ ⎢ ⎥ ⎢ -z₁⋅α + z₂⋅β⎥ ⎢ 1 ────────────⎥ ⎣ α - β ⎦ In [14]: Z1 = Matrix([z1,1]) In [15]: Z1 Out[15]: ⎡z₁⎤ ⎢ ⎥ ⎣1 ⎦ In [16]: 透視*Z1 Out[16]: ⎡z₁⋅α⋅β⋅(-z₁ + z₂)⎤ ⎢─────────────────⎥ ⎢ α - β ⎥ ⎢ ⎥ ⎢ -z₁⋅α + z₂⋅β⎥ ⎢z₁ + ────────────⎥ ⎣ α - β ⎦ In [17]: ((透視*Z1)[0] / (透視*Z1)[1]).simplify() Out[17]: z₁⋅α In [18]: Z2 = Matrix([z2,1]) In [19]: ((透視*Z2)[0] / (透視*Z2)[1]).simplify() Out[19]: z₂⋅β </pre> <span style="color: #666699;">先知 □ ○ 其意義較好的吧◎</span> <span style="color: #666699;">就](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-a0246f727c5b55b7e33eea694f08dab2_l3.png) l
l z_1 \Rightarrow z_1+z_t , \ z_2 \Rightarrow z_2+z_t, \ z \Rightarrow z+z_t
z_1 \Rightarrow z_1+z_t , \ z_2 \Rightarrow z_2+z_t, \ z \Rightarrow z+z_t z_1 \Rightarrow e^{i \phi} z_1 , \ z_2 \Rightarrow e^{i \phi} z_2, \ z \Rightarrow e^{i \phi}z
z_1 \Rightarrow e^{i \phi} z_1 , \ z_2 \Rightarrow e^{i \phi} z_2, \ z \Rightarrow e^{i \phi}z z_1 \Rightarrow {z_1}^{*} , \ z_2 \Rightarrow {z_2}^{*}, \ z \Rightarrow z^{*}
z_1 \Rightarrow {z_1}^{*} , \ z_2 \Rightarrow {z_2}^{*}, \ z \Rightarrow z^{*} {z_1}^{'} = \alpha z_1, \ {z_2}^{'} = \beta z_2, \ z^{'} = \gamma z
{z_1}^{'} = \alpha z_1, \ {z_2}^{'} = \beta z_2, \ z^{'} = \gamma z z^{'} = \frac{\alpha \cdot \beta \cdot z \cdot (z_2-z_1) }{(\alpha - \beta) z + (\beta \cdot z_2 - \alpha \cdot z_1)}}$
z^{'} = \frac{\alpha \cdot \beta \cdot z \cdot (z_2-z_1) }{(\alpha - \beta) z + (\beta \cdot z_2 - \alpha \cdot z_1)}}$


![Rendered by QuickLaTeX.com ipython3 Python 3.4.2 (default, Oct 19 2014, 13:31:11) Type "copyright", "credits" or "license" for more information. IPython 2.3.0 -- An enhanced Interactive Python. ? -> Introduction and overview of IPython's features. %quickref -> Quick reference. help -> Python's own help system. object? -> Details about 'object', use 'object??' for extra details. In [1]: from sympy import * In [2]: init_printing() In [3]: a,b,z1,z2,z,zp = symbols('a,b,z1,z2,z,zp') In [4]: S = solve(zp - ((zp-a*z1)/(b*z2-a*z1))/((z-z1)/(z2-z1))*b*z , zp) In [5]: S Out[5]: ⎡ a⋅b⋅z⋅(-z₁ + z₂) ⎤ ⎢───────────────────────⎥ ⎣a⋅z - a⋅z₁ - b⋅z + b⋅z₂⎦ In [6]: (S[0].subs(z,z1)).simplify() Out[6]: a⋅z₁ In [7]: (S[0].subs(z,z2)).simplify() Out[7]: b⋅z₂ In [8]: </pre> <span style="color: #666699;">彷彿只剩『符號代換』,果然如是矣◎</span> <span style="color: #666699;">提筆揮灑尚不曉</span> <span style="color: #666699;">](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-417362182f296929ad379c3eb4a6c78e_l3.png) z^{'} = \frac{\alpha \cdot \beta \cdot z \cdot (z_2-z_1) }{(\alpha - \beta) z + (\beta \cdot z_2 - \alpha \cdot z_1)}}
z^{'} = \frac{\alpha \cdot \beta \cdot z \cdot (z_2-z_1) }{(\alpha - \beta) z + (\beta \cdot z_2 - \alpha \cdot z_1)}} \because \alpha = \beta, \ \therefore \ z^{'} = \alpha \cdot z = \beta \cdot z
\because \alpha = \beta, \ \therefore \ z^{'} = \alpha \cdot z = \beta \cdot z 








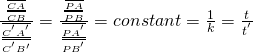 。
。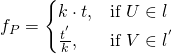 。
。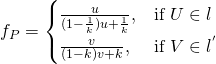 。
。